mọi người ơi giúp mình bài 5 với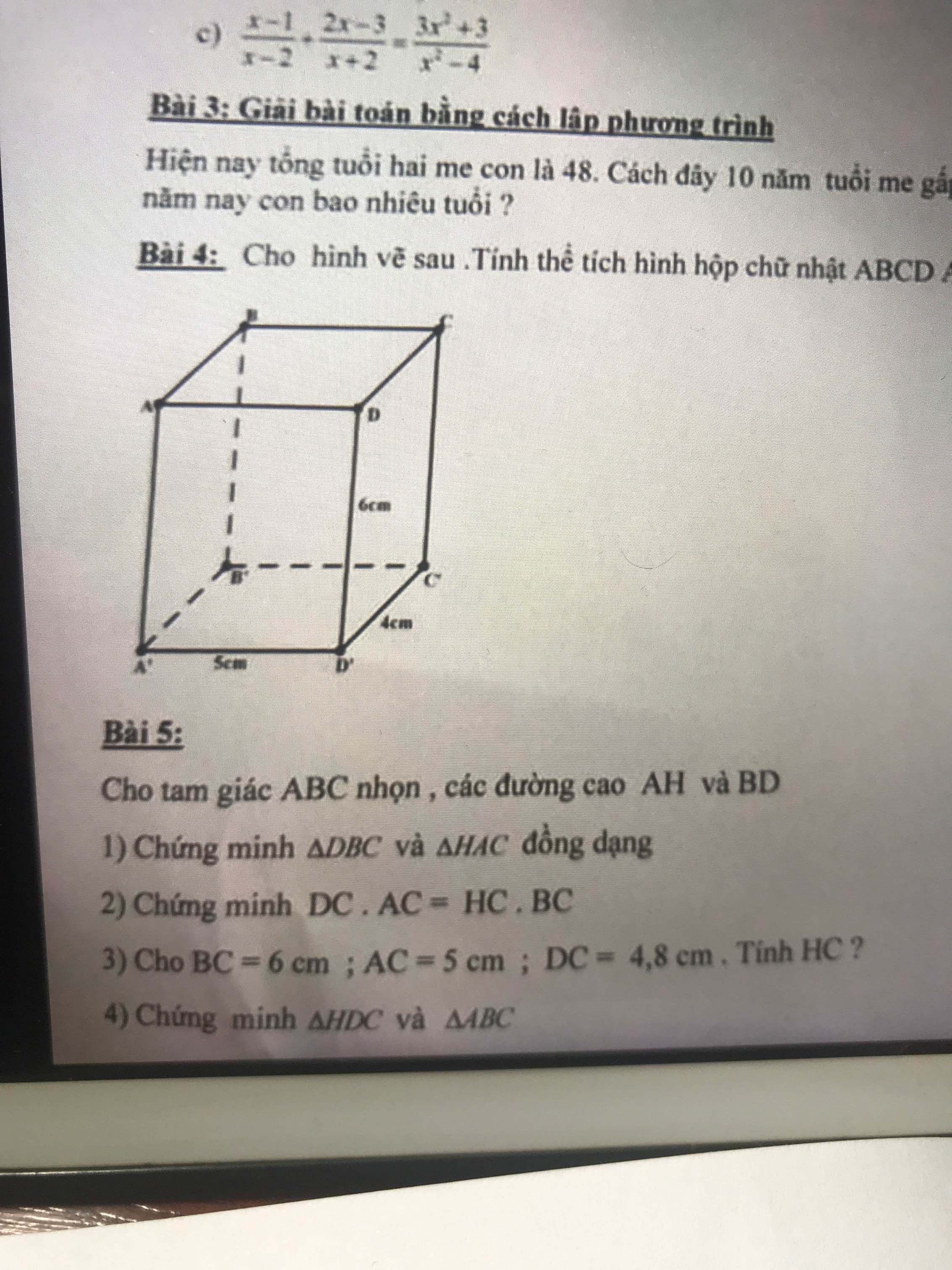
NN
Những câu hỏi liên quan
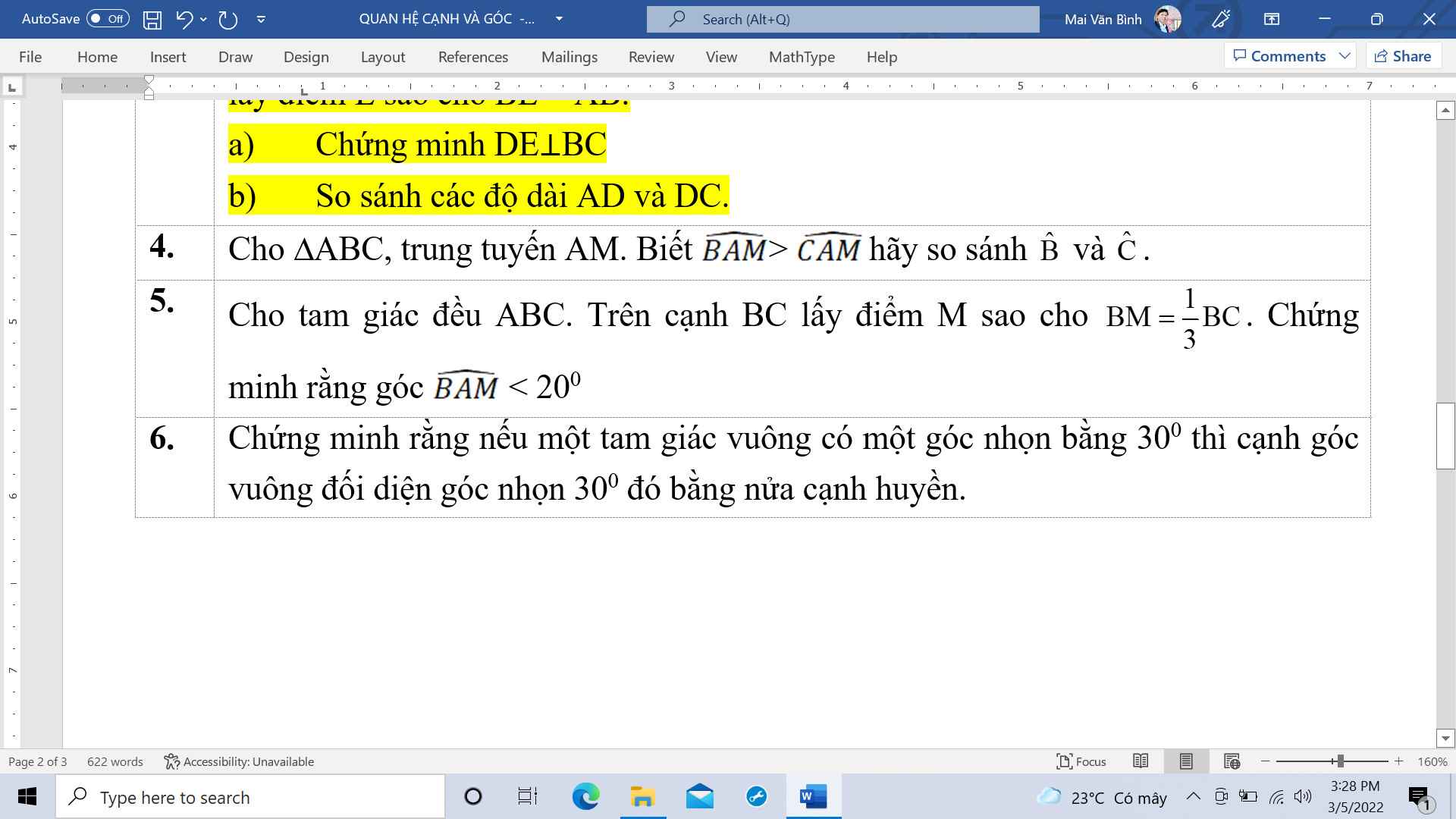
mọi người ơi giúp mình bài 4 5 6 với ạ mình đang cần gấp
Mọi người ơi giúp mình giải bài 1 tiết 99 trong sách bài tập toán lớp 5 tập 2 với
Thank mọi người
- Ta nhận thấy độ dài sợi dây thép chính bằng chu vi của 4 nửa hình tròn.
- Ghép 4 nửa hình tròn, ta được 2 hình tròn mới có đường kính là 9 cm.
Chu vi của mỗi hình tròn là:
9 x 3,14 = 28,26 ( cm )
Độ dài sợi dây thép là:
28,26 x 2 = 56,52 ( cm )
Đáp số: 56,52 cm.
Bài này phải không bạn?
k mình nhé!
Bài này mình làm đúng rồi đó!
Đúng 0
Bình luận (0)
mọi người ơi giúp mình hiểu cách tính này với:
1- 1/5 - 1/6= 19/30
mình không biết tại sao ra 19/30, giải thích giúp mình để mình hiểu bài hơn nha. mình cảm ơn mọi người
Mình tính từng cái ra nha, từng cái sẽ ra được kết quả của phép tính:
\(1-\dfrac{1}{5}-\dfrac{1}{6}\)
\(=\left(1-\dfrac{1}{5}\right)-\dfrac{1}{6}\)
\(=\left(\dfrac{5}{5}-\dfrac{1}{5}\right)-\dfrac{1}{6}\)
\(=\dfrac{4}{5}-\dfrac{1}{6}\)
\(=\dfrac{24}{30}-\dfrac{5}{30}\)
\(=\dfrac{19}{30}\)
Đúng 3
Bình luận (0)
Mọi người ơi mọi người giúp mình hoàn thành bài thi nhé mình chỉ có 5 lần thoát ra thôi mọi người giúp mình nhé
ủa đề đâu,sao ko có đề làm sao mik giải được
Ok bạn, bạn hỏi đi
@Đặng Trần Thanh Xuân
From Ŧŗịɳħ Đüć Ťĭếɳ
Lát nữa người ta mở đề thì mình sẽ hỏi các bạn các bạn trả lời giúp mình nhé
Xem thêm câu trả lời
mọi người ơi giúp mình bài này với , làm đc bài nào thì giúp mình nha :
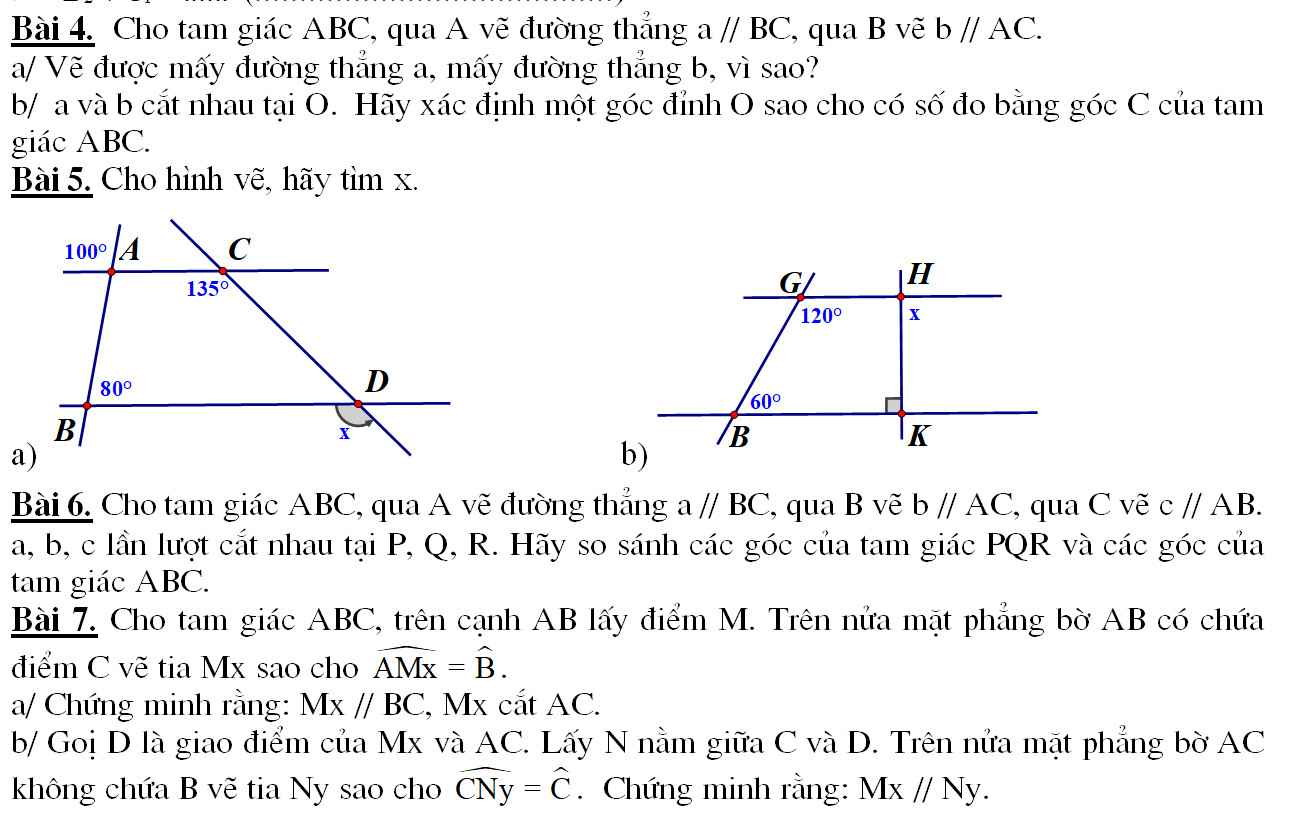
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
Đúng 1
Bình luận (0)
Mọi người ơi giúp mình làm từ bài 44 đến 50 với nha mọi người mình cảm ơn nhiều
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
Đúng 3
Bình luận (1)
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)
Đẳng thức xảy ra <=> a=b=c
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi, mình chưa biết giải bài này:(( Mọi người giúp mình với, mình cảm ơn rất nhiều ạ😭 
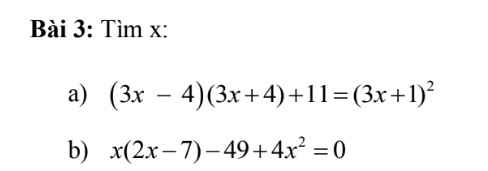
giúp mình bài này với mọi người ơi :((
b: \(\Leftrightarrow\left(2x-7\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)

giúp mình bài này với mọi người ơi
a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
Đúng 1
Bình luận (0)
a) Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì AED=AFD=EAF=900AED=AFD=EAF=900 nên AEDF là hcn
b) Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c) Vì D là trung điểm BC và AK và BAC=900BAC=900 nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A
Đúng 1
Bình luận (1)





