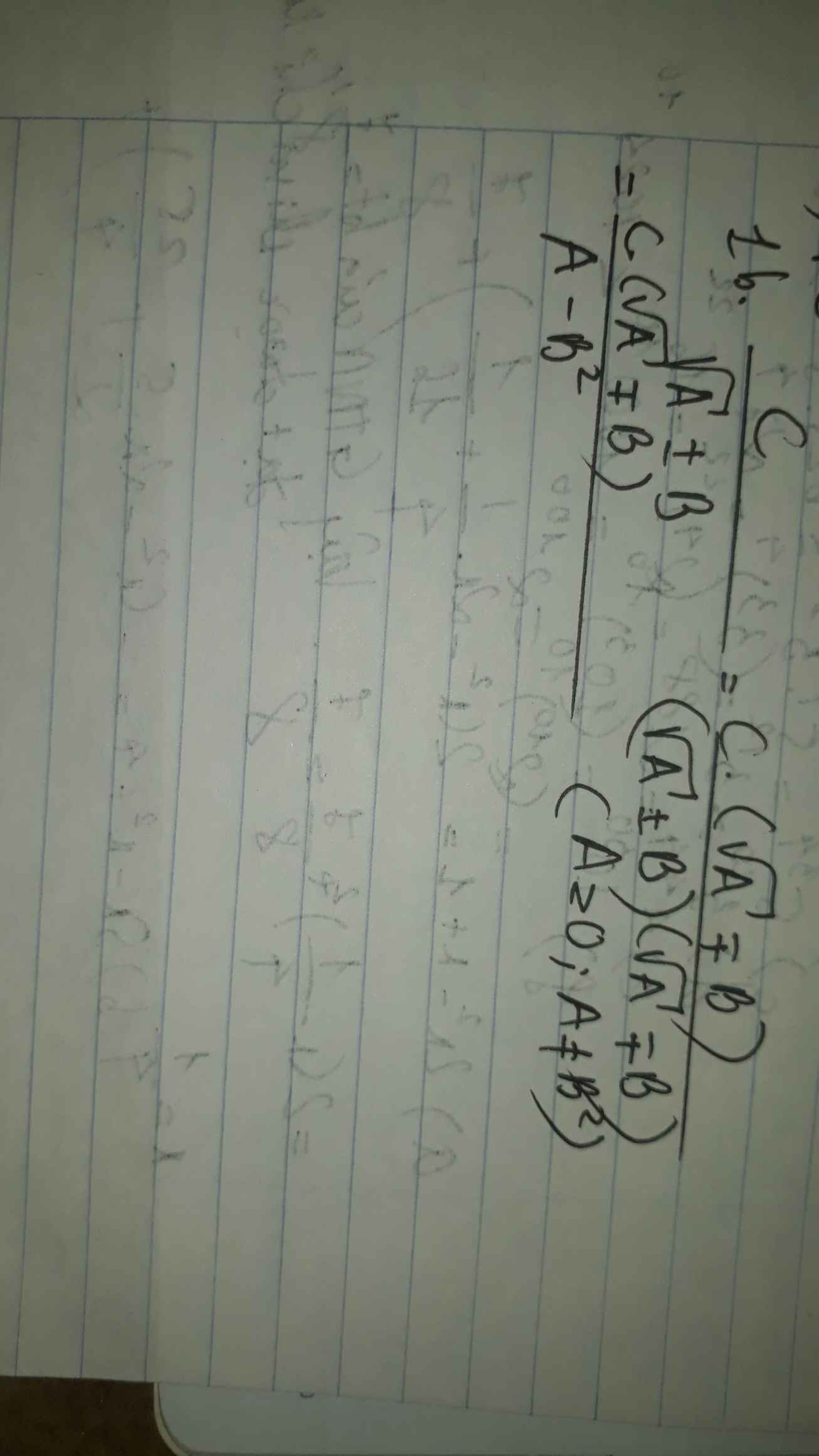giúp m bài 1b vs ạ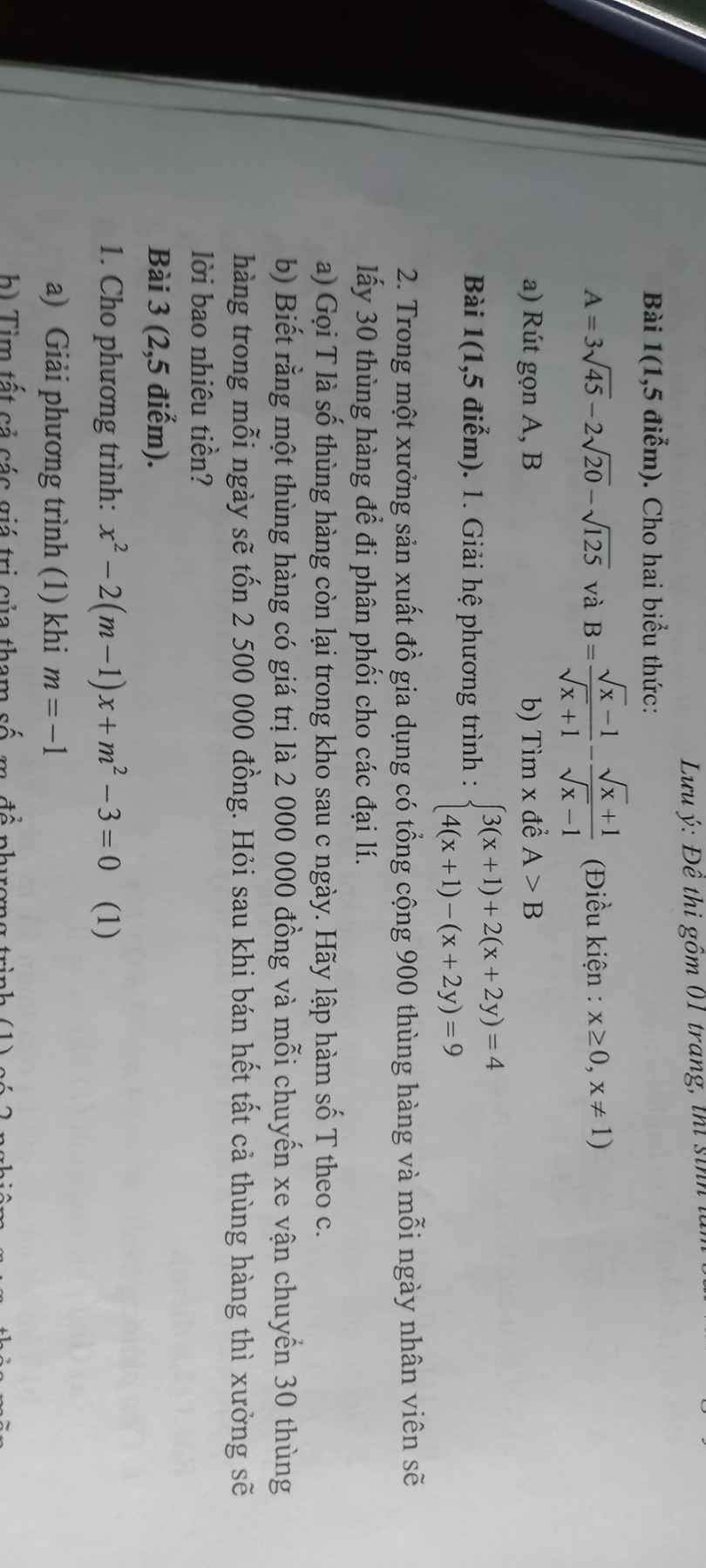
H24
Những câu hỏi liên quan
Giúp em bài 1b vs 1C vs ạ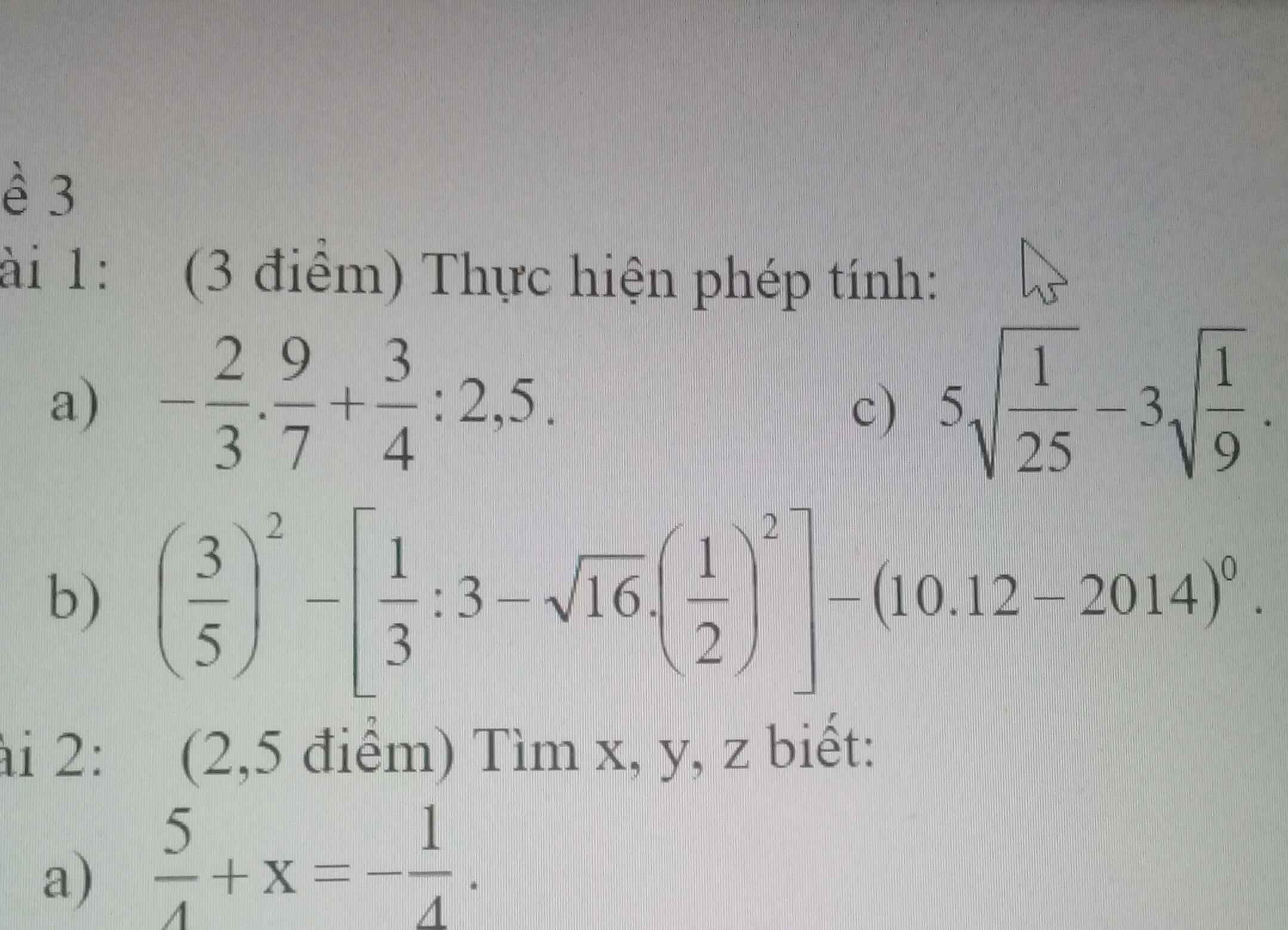
c: \(=5\cdot\dfrac{1}{5}-3\cdot\dfrac{1}{3}=0\)
Đúng 0
Bình luận (0)
\(\text{b)}\left(\dfrac{3}{5}\right)^2-\left[\dfrac{1}{3}:3-\sqrt{16}.\left(\dfrac{1}{2}\right)^2\right]-\left(10.12-2014\right)^0\)
\(=\dfrac{9}{25}-\left[\dfrac{1}{9}-1\right]-1\)
\(=\dfrac{9}{25}-\left(\dfrac{-8}{9}\right)-1\)
\(=\dfrac{281}{225}-1\)
\(=\dfrac{56}{225}\)
\(\text{c)}5\sqrt{\dfrac{1}{25}}-3\sqrt{\dfrac{1}{9}}\)
\(=5.\dfrac{1}{5}-3.\dfrac{1}{3}\)
\(=1-1\)
\(=0\)
Đúng 4
Bình luận (0)
Giúp em bài 1b ạ
\(f\left(x\right)+g\left(x\right)=x^2-3x+2\)
\(\Leftrightarrow x^3-2x^2+x-1+g\left(x\right)=x^2-3x+2\)
\(\Leftrightarrow g\left(x\right)=-x^3+3x^2-4x+3\)
Đúng 1
Bình luận (0)
Giúp em câu 1b và bài 4 với ạ

1B:
a: Ta có: \(N=\sqrt{8}+\sqrt{32}+\sqrt{108}-\sqrt{27}\)
\(=2\sqrt{2}+4\sqrt{2}+6\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{2}+3\sqrt{3}\)
b: Ta có: \(M=\dfrac{2}{2+\sqrt{3}}-\dfrac{1}{2-\sqrt{3}}\)
\(=4-2\sqrt{3}-2-\sqrt{3}\)
\(=2-3\sqrt{3}\)
Đúng 2
Bình luận (0)
Giúp mình câu 1b với bài 2 với ạ, cần gấp lắm, cảm ơn ạ
1b)
Song song => (d): x-y +a =0
Vì d đi qua C(2;-2) => 2- (-2)+a=0
<=>a=4
=> d: x-y+4=0
Đúng 0
Bình luận (0)
giúp mk vs ạ
a)| x-13| - |2x +9 | = 1
b) |3x + 2| - | x+5|= -2x
nhanh hộ mk ạ
M.n giúp mk nha mk Câu 1b vs Câu 2b nha
MK ĐAG CẦN GẤP Ạ
cảm ưn nhìu
a: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C
Đúng 0
Bình luận (0)
1B,2B,3A,3B,4A mọi người giúp em làm bài này với ạ
1B,2B,3A,3B,4A mọi người ơi giúp em bài này với ạ 
giúp mình phần 1 B và 1b , với cả bài 2 với ạ. Mình cảm ơn
1b) \(C=\sqrt{81a}-\sqrt{144a}+\sqrt{36a}\left(a\ge0\right)=8\sqrt{a}-12\sqrt{a}+6\sqrt{a}=2\sqrt{a}\)
Bài 2:
a),b) \(P=\left(\dfrac{1}{1-\sqrt{a}}-\dfrac{1}{1+\sqrt{a}}\right)\left(\dfrac{1}{\sqrt{a}}+1\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{1+\sqrt{a}-1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}.\dfrac{\sqrt{a}+1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{1-\sqrt{a}}.\dfrac{1}{\sqrt{a}}=\dfrac{2}{1-\sqrt{a}}\)
c) \(P=\dfrac{2}{1-\sqrt{a}}=\dfrac{2}{1-\sqrt{4}}=\dfrac{2}{1-2}=-2\)
d) \(P=\dfrac{2}{1-\sqrt{a}}=9\)
\(\Rightarrow-9\sqrt{a}+9=2\Rightarrow\sqrt{a}=\dfrac{7}{9}\Rightarrow a=\dfrac{49}{81}\left(tm\right)\)
Đúng 1
Bình luận (0)