Ai biết giải giúp em đề 3 với ạ gấp lắm ạ 😥
SH
Những câu hỏi liên quan
Giúp em bài này với ạ, gấp lắm ạ😥
Giúp mình với ạ, gấp lắm ạ😥😥
a.
\(0< x< \dfrac{\pi}{2}\Rightarrow cosx>0\Rightarrow cosx=\sqrt{1-sin^2x}=\dfrac{\sqrt{6}}{3}\)
\(cos\left(x+\dfrac{\pi}{3}\right)=cosx.cos\left(\dfrac{\pi}{3}\right)-sinx.sin\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{6}-3}{6}\)
b.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow sinx< 0\)
\(\Rightarrow sinx=-\sqrt{1-cos^2x}=-\dfrac{5}{13}\)
\(B=sin\left(\dfrac{\pi}{3}-x\right)=sin\left(\dfrac{\pi}{3}\right).cosx-cos\left(\dfrac{\pi}{3}\right).sinx=...\) (bạn tự thay số bấm máy)
Đúng 3
Bình luận (0)
c.
\(A=cos^2x+cos^2y+2cosx.cosy+sin^2x+sin^2y+2sinx.siny\)
\(=\left(cos^2x+sin^2x\right)+\left(cos^2y+sin^2y\right)+2\left(cosx.cosy+sinx.siny\right)\)
\(=1+1+2cos\left(x-y\right)\)
\(=2+2cos\left(\dfrac{\pi}{3}\right)=...\)
d.
\(B=cos^2x+sin^2y+2cosx.siny+cos^2y+sin^2x-2sinx.cosy\)
\(=\left(cos^2x+sin^2x\right)+\left(cos^2y+sin^2y\right)-2\left(sinx.cosy-cosx.siny\right)\)
\(=2-2sin\left(x-y\right)=2-2sin\left(\dfrac{\pi}{3}\right)=...\)
Đúng 2
Bình luận (0)
Mọi người giúp mình câu ba với ạ, cần gấp lắm ạ!! 😥😥😥
Anh nghĩ với bài kiểm tra em nên tự làm nhé.
Đúng 1
Bình luận (1)
Giúp mình với ạ, mình cần gấp lắm😥😥
a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow1+2sinx.cosx=t^2\Rightarrow2sinx.cosx=t^2-1\)
Phương trình trở thành:
\(3t=2\left(t^2-1\right)\)
\(\Leftrightarrow2t^2-3t-2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2>\sqrt{2}\left(loại\right)\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{8}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(1+\dfrac{sinx}{cosx}=2\sqrt{2}sinx\)
\(\Rightarrow sinx+cosx=2\sqrt{2}sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{3\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\)
Đúng 0
Bình luận (0)
c.
\(\Leftrightarrow1+sinx+cosx+sinx.cosx=2\)
\(\Leftrightarrow sinx+cosx+sinx.cosx=1\)
Đặt \(sinx+cosx=t\in\left[-\sqrt[]{2};\sqrt{2}\right]\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t+\dfrac{t^2-1}{2}=1\)
\(\Leftrightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
SÓ. Giúp em giải chi tiết câu 23,34 với ạ🙏🙏😥😥😥. Cần gấp
23.
Gọi I là trung điểm MN \(\Rightarrow I\left(3;3\right)\)
\(\Rightarrow\overrightarrow{IN}=\left(2;-1\right)\Rightarrow IN=\sqrt{5}\)
Phương trình đường tròn đường kính MN, nhận I là tâm và có bán kính \(R=IN\) là:
\(\left(x-3\right)^2+\left(y-3\right)^2=5\)
Thay tọa độ E vào pt ta được:
\(\left(x-3\right)^2+4=5\Rightarrow\left(x-3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\) \(\Rightarrow x_1x_2=8\)
Cả 4 đáp án của câu này đều sai
Đúng 1
Bình luận (0)
24.
Gọi \(M\left(x;y\right)\) là 1 điểm bất kì thuộc \(\Delta\)
Do \(\Delta\) là đường phân giác của góc tạo bởi d và k nên:
\(d\left(M;d\right)=d\left(M;k\right)\Leftrightarrow\dfrac{\left|2x+y\right|}{\sqrt{2^2+1^2}}=\dfrac{\left|x+2y-3\right|}{\sqrt{1^2+2^2}}\)
\(\Leftrightarrow\left|2x+y\right|=\left|x+2y-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+y=x+2y-3\\2x+y=-x-2y+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y+3=0\\x+y-1=0\end{matrix}\right.\)
- Với \(x-y+3=0\), ta có:
\(\left(x_E-y_E+3\right)\left(x_F-y_F+3\right)=2.1=2>0\Rightarrow E;F\) nằm cùng phía so với \(x-y+3=0\) (thỏa mãn)
- Với \(x+y-1=0\) ta có:
\(\left(x_E+y_E-1\right)\left(x_F+y_F-1\right)=2.7=14>0\Rightarrow E;F\) nằm cùng phía so với \(x+y-1=0\) (thỏa mãn)
Vậy cả đáp án A và D đều đúng
Tương tự như câu 23, câu 24 đề bài tiếp tục sai
Đúng 1
Bình luận (0)
Ai giúp mình giải bài này với ạ😥😥😥
`sin(2x-π/3)+1=0`
`<=>sin(2x-π/3)=-1`
`<=>2x-π/3=-π/2=k2π`
`<=>x=(5π)/12+kπ (k \in ZZ)`
Có: `-2020π < (5π)/12+kπ < 2020π`
`<=> -2020 < 5/12+k<2020`
`<=>-2020-5/12 <k<2020+5/12`
`=> k \in {-2020;.....;2020}`
`=>` Có `4041` giá trị của `k` thỏa mãn.
Đúng 2
Bình luận (0)
Mn giúp mình vời ạ, mình cần gấp lắm😥😥!!!
a.
\(90^0< a< 180^0\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{2\sqrt{2}}{3}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{\sqrt{2}}{4}\)
b.
\(0< a< 90^0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
c.
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{3cosa}{sina}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{sin^2a+3cos^2a}{sin^2a+cos^2a}=1+2cos^2a=\dfrac{17}{8}\)
d.
\(A=\dfrac{\dfrac{cosa}{sina}+\dfrac{3sina}{cosa}}{\dfrac{2cosa}{sina}+\dfrac{sina}{cosa}}=\dfrac{cos^2a+3sin^2a}{2cos^2a+sin^2a}=\dfrac{cos^2a+3\left(1-cos^2a\right)}{2cos^2a+\left(1-cos^2a\right)}\)
\(=\dfrac{3-2cos^2a}{1+cos^2a}=\dfrac{19}{13}\)
Đúng 1
Bình luận (0)
e.
\(B=\dfrac{\dfrac{3cosa}{sina}+\dfrac{2sina}{cosa}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{3cos^2a+2sin^2a}{sin^2a+cos^2a}=3\left(1-sin^2a\right)+2sin^2a\)
\(=3-sin^2a=\dfrac{26}{9}\)
f.
\(C=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}=\dfrac{2tana+3}{tana+1}=\dfrac{7}{3}\)
g.
\(C=\dfrac{\dfrac{3sina}{sina}-\dfrac{4cosa}{sina}}{\dfrac{cosa}{sina}-\dfrac{2sina}{sina}}=\dfrac{3-4cota}{cota-2}=1+\sqrt{5}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp em với ạ. Cần gấp 😥😥😥😥🙏🙏🙏🙏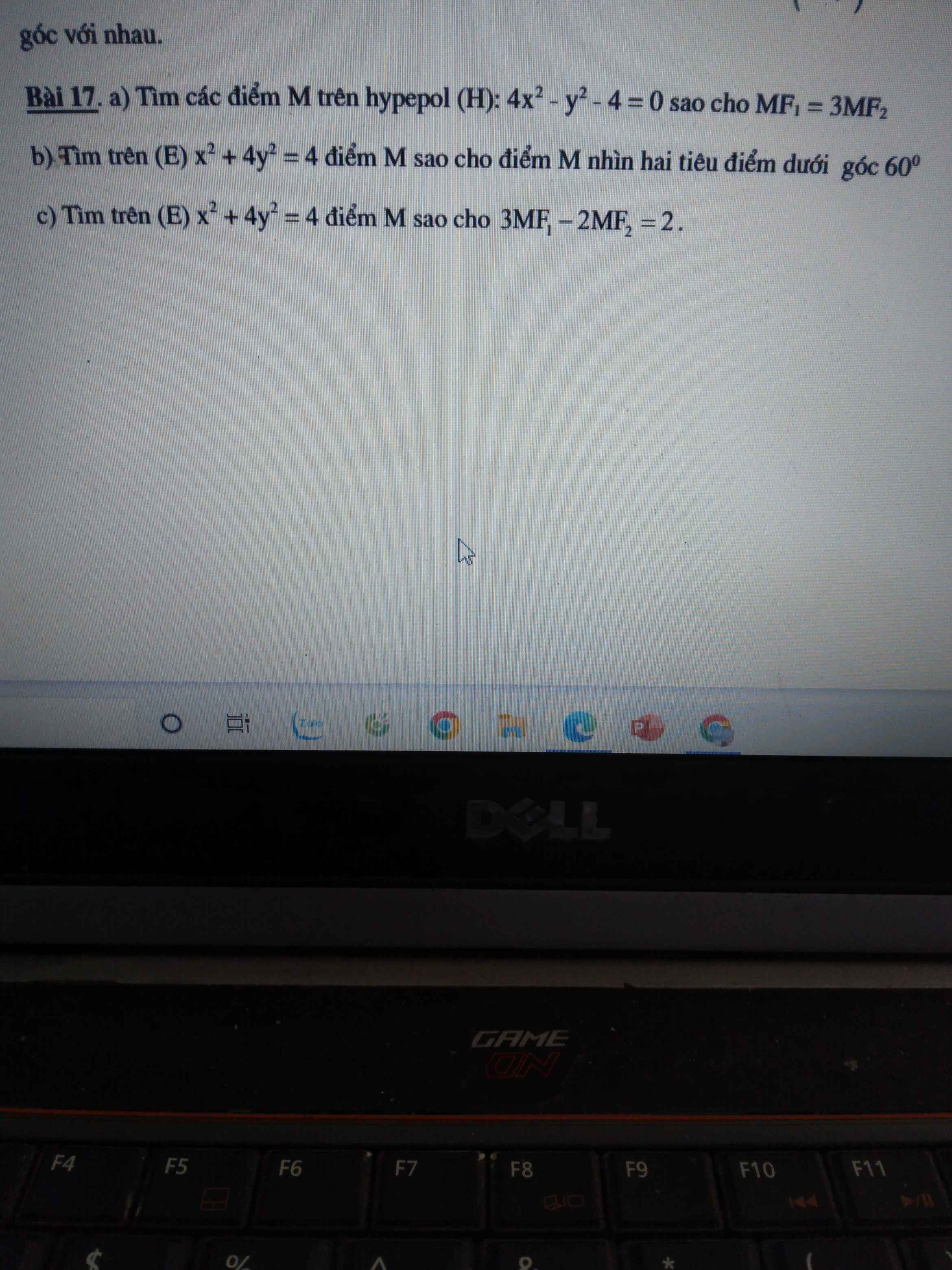
 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn

