cho tam giác ABC nhọn.chứng minh:
tan2A+tan2B+tan2C>4(cot2A+cot2B+cot2C)
Cho tam giác ABC thỏa mãn: cos 2 A + cos 2 B sin 2 A + sin 2 B = 1 2 ( c o t 2 A + c o t 2 B ) Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân tại C
C. Tam giác ABC là tam giác cân tại A
D. tam giác ABC là tam giác nhọn
Chọn B.
Ta có:
![]()
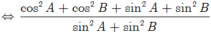
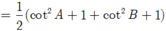
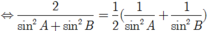
![]()
Suy ra ( sin2A - sin2B)2 = 0
Lại có: sin2A = sin2B khi và chỉ khi
![]() hay a = b
hay a = b
Suy ra tam giác ABC cân tại C.
Cho tam giác ABC vuông tại A (AB < AC), có đường cao AH (H thuộc BC)
a) Cho biết HB = 3cm, HC = 9cm. Tính AH, AB, AC?
b) Chứng minh: tan2C + cot2C = HC/HB + HC/HB (không sử dụng số liệu ở câu a để chứng minh).
Cho tam giác ABC vuông tại A (AB < AC), có đường cao AH (H thuộc BC)
a) Cho biết HB = 3cm, HC = 9cm. Tính AH, AB, AC?
b) Chứng minh: tan2C + cot2C = HC/HB + HC/HB (không sử dụng số liệu ở câu a để chứng minh).
Mình giải bài mà bí quá, SOS xin các thần thánh cao nhân cứu giúp!!!
a: BC=BH+CH
=3+9
=12(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=3\cdot9=27\)
=>\(AH=3\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{3\cdot12}=6\left(cm\right)\\AC=\sqrt{9\cdot12}=6\sqrt{3}\left(cm\right)\end{matrix}\right.\)
b: \(tan^2C+cot^2C\)
\(=\left(\dfrac{AC}{AB}\right)^2+\left(\dfrac{AB}{AC}\right)^2\)
\(=\dfrac{AC^2}{AB^2}+\dfrac{AB^2}{AC^2}\)
\(=\dfrac{HC\cdot BC}{HB\cdot BC}+\dfrac{HB\cdot BC}{HC\cdot CB}\)
\(=\dfrac{HC}{HB}+\dfrac{HB}{HC}\)
Cho tam giác ABC vuông tại A, biết AC = 20cm ; BC = 30cm.
a/ Giải tam giác vuông ABC ( Số đo của góc làm tròn đến độ )
b/ Kẻ đường cao AH của ΔABC. Tính AH ; CH.
c/ Chứng minh : tan2C = \(\dfrac{BH}{CH}\)
a, \(AB=\sqrt{BC^2-AC^2}=10\sqrt{5}\left(cm\right)\)
\(\cos B=\dfrac{AC}{BC}=\dfrac{2}{3}\approx48^0\Rightarrow\widehat{B}\approx48^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx90^0-48^0=42^0\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{20\sqrt{5}}{30}\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{40}{3}\left(cm\right)\end{matrix}\right.\)
Tam giác ABC nhọn.Chứng minh:
a)sin A+cos A>1
b)Nếu BC=a,góc B=45 độ,góc C=60 độ.Tính diện tích tam giác ABC theo a
c)Vẽ đường cao AH,M,N là hình chiếu của H trên AB,AC.Cm:\(AH=\frac{BC}{cotB+cotC}\)
+) \(\frac{1}{MH^2}+\frac{1}{NH^2}=\frac{1}{BH^2}+\frac{1}{CH^2}\)
+)MN = AH . sin A
Cho đường thẳng AOB.Trên cùng một nửa mặt phẳng bờ AB vẽ các tia OC và OD sao cho AOC=BOD.Gọi OE là tia đối của tia OD
a) Nếu AOC và BOD đều nhọn.Chứng tỏ rằng tia OA là tia phân giác của COE
b) Nếu AOC và BOD đều tù.Tìm tia phân giác của COE
Cho tam giác ABC có AB:AC:BC=3:4:5.chu vi tam giác ABC=120cm,vậy diện tích tam giác ABC là?
Gọi ba cạnh tam giác là a ; b ; c
Theo bài ra ta có a : b : c = 3 : 4 : 5 và a + b + c = 120
Tự giải a ; b ; c kq : a = 30 ; b = 40 ; c = 50
Xét \(a^2+b^2=\left(30\right)^2+\left(40\right)^2=900+1600=2500=50^2=c^2\)
=> tam giác ABC vuông tại A => diện tich tam giác
cho tam giác ABC có AB:AC:BC=4:5:6. cho tam giác MNP đồng dạng với tam giác ABC với chu vi =90cm . tính các cạnh của tam giác MNP
Cho tam giác ABC thỏa \(\dfrac{a^3+b^3+c^3}{abc}+\dfrac{2r}{R}=4\) chứng minh tam giác ABC là tam giác đều
Ta có \(S=\dfrac{abc}{4R}=pr=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(\Rightarrow S^2=\dfrac{abcpr}{4R}=p\left(p-a\right)\left(p-b\right)\left(p-c\right)\)
\(\Rightarrow\dfrac{2r}{R}=\dfrac{\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}{abc}\)
Theo giả thiết \(\dfrac{a^3+b^3+c^3}{abc}+\dfrac{2r}{R}=4\)
\(\Leftrightarrow\dfrac{a^3+b^3+c^3}{abc}+\dfrac{\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}{abc}=4\)
\(\Leftrightarrow a^3+b^3+c^3+\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)=4abc\)
\(\Leftrightarrow a^2b+ab^2+b^2c+bc^2+c^2a+ca^2=6abc\left(1\right)\)
Áp dụng BĐT AM-GM:
\(a^2b+ab^2+b^2c+bc^2+c^2a+ca^2\ge6abc\)
\(\Rightarrow\left(1\right)\) đúng
Đẳng thức xảy ra khi \(a=b=c\)
\(\Leftrightarrow\Delta ABC\) đều