2x-4X+1=0 tìm nghiệm pt thế nào thế ạ
CM
Những câu hỏi liên quan
mx^2+2(m-1)x+4m=0 Tìm m để pt có 2 nghiệm thế nào ạ
pt này có cả bậc 3 thì phải làm thế nào ạ:
\(x^4+3x^3+mx^2+3x+1=0\left(1\right)\)
tìm m để pt(1) có 4 nghiệm phân biệt
Với \(x=0\) ko phải nghiệm
Với \(x\ne0\) chia 2 vế cho \(x^2\) ta được:
\(x^2+\dfrac{1}{x^2}+3x+\dfrac{3}{x}+m=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)+m-2=0\) (1)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow x^2-tx+1=0\) (2)
(2) có 2 nghiệm pb khi và chỉ khi:
\(\Delta=t^2-4>0\Rightarrow\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
Khi đó (1) trở thành:
\(t^2+3t+m-2=0\) (3)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (3) có 2 nghiệm pb thỏa mãn \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
(3) \(\Leftrightarrow t^2+3t-2=-m\)
Đặt \(f\left(t\right)=t^2+3t-2\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=8\)
Đồ thị hàm \(f\left(t\right)\):
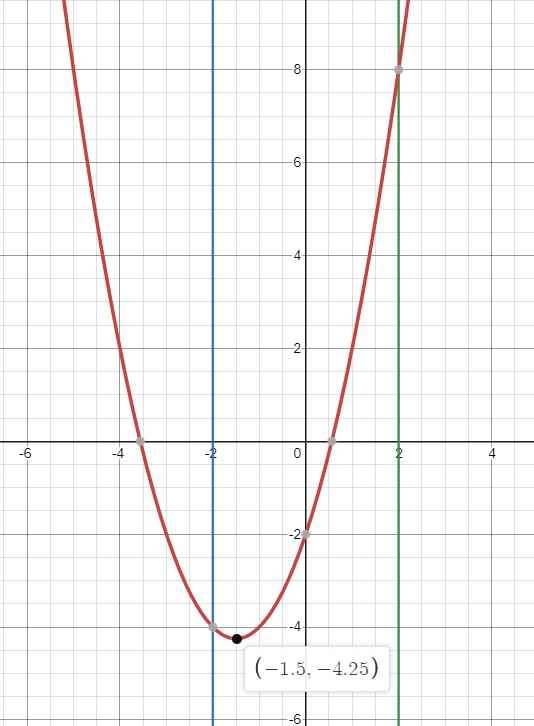
Từ đồ thị ta thấy \(y=-m\) cắt \(y=f\left(t\right)\) tại 2 điểm đều nằm ngoài \(\left[-2;2\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}-\dfrac{17}{4}< -m< -4\\-m>8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4< m< \dfrac{17}{4}\\m< -8\end{matrix}\right.\)
Đúng 2
Bình luận (1)
1) Tìm m để pt : -2x2 - 3x - m + 1 = 0 có 2 nghiệm âm phân biệt.
2) Tìm m để pt : -3x2 - 4x -2m + 1 = 0 có 2 nghiệm âm.
MN GIÚP E BÀI NÀY VỚI Ạ. E ĐANG CẦN GẤP Ạ.
\(1,\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-3\right)^2-4\left(-2\right)\left(-m+1\right)>0\\x_1+x_2=\dfrac{3}{-2}< 0\\x_1x_2=\dfrac{-m+1}{-2}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17-8m>0\\-m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{17}{8}\\m>1\end{matrix}\right.\Leftrightarrow1< m< \dfrac{17}{8}\)
\(2,\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-4\right)^2-4\left(-3\right)\left(-2m+1\right)\ge0\\x_1+x_2=\dfrac{4}{-3}< 0\\x_1x_2=\dfrac{-2m+1}{-3}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}28-24m\ge0\\-2m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{7}{6}\\m>\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< m\le\dfrac{7}{6}\)
Đúng 2
Bình luận (1)
tìm m để 1 nghiệm của phương trình 2x^2 - 13x + 2m = 0 gấp dôi 1 nghiệm của pt x^2 - 4x + m = 0
cho pt 2x^2=4x+5(m-1)=0. Tìm m để pt có 2 nghiệm phân biệt x1,x2 nhỏ hơn 3
tìm m để pt có nghiệm thuộc \(\left[-1;1\right]\)
x^4+2x^3+5x^2+4x-1-m=0
\(x^4+2x^3+5x^2+4x-1-m=0\)
\(\Leftrightarrow\left(x^2+x\right)^2+4\left(x^2+x\right)-1-m=0\left(1\right)\)
\(đặt:x^2+x=t\ge\dfrac{-\Delta}{4a}=-\dfrac{1}{4}\)
\(\left(1\right)\Leftrightarrow t^2+4t-1-m=0\) có nghiệm trên \([-\dfrac{1}{4};\text{+∞})\)
\(f\left(t\right)=t^2+4t-1=m\)
\(f\left(-\dfrac{b}{2a}\right)=-5\)
\(f\left(-\dfrac{1}{4}\right)=-\dfrac{31}{16}\Rightarrow m\ge-\dfrac{31}{16}\Rightarrow\left[{}\begin{matrix}t=\dfrac{-b}{2a}=-2\Rightarrow x^2+x+2=0\left(vô-nghiệm\right)\left(loại\right)\\\left\{{}\begin{matrix}t1=\dfrac{-4+\sqrt{20+4m}}{2}=-2+\sqrt{5+m}\\t2=\dfrac{-4-\sqrt{20+4m}}{2}=-2-\sqrt{5+m}\end{matrix}\right.\end{matrix}\right.\)
\(x^2+x=t1=-2+\sqrt{5+m}\Leftrightarrow f\left(x\right)=x^2+x+2=\sqrt{5+m}\) có nghiệm thuộc \(\left[-1;1\right]\)
\(\Rightarrow f\left(-\dfrac{b}{2a}\right)=\dfrac{7}{4}\)
\(f\left(-1\right)=2;f\left(1\right)=4\)
\(\Rightarrow\dfrac{7}{4}\le\sqrt{5+m}\le4\Leftrightarrow\dfrac{-31}{16}\le m\le11\)
\(x^2+x=t2=-2-\sqrt{5+m}\Leftrightarrow f\left(x\right)=x^2+x+2=-\sqrt{5+m}\)
có nghiệm trên \(\left[-1;1\right]\)
\(x^2+x+2>0\Rightarrow x^2+x+2=-\sqrt{5+m}< 0\left(vô-lí\right)\Rightarrow vô-nghiệm\forall m\)
\(\Rightarrow\dfrac{-31}{16}\le m\le11\) thì pt có nghiệm thuộc \(\left[-1;1\right]\)
Đúng 0
Bình luận (0)
1. Tìm \(m\in\left[-10;10\right]\) để pt \(\left(x^2-2x+m\right)^2-2x^2+3x-m=0\) có 4 ng pb
2. Cho biết x1,x2 là nghiệm của pt \(x^2-x+a=0\) và x3,x4 là nghiệm của pt \(x^2-4x+b=0\) . Biết rằng \(\dfrac{x2}{x1}=\dfrac{x3}{x2}=\dfrac{x4}{x3}\), b >0 . Tìm a
1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Đúng 3
Bình luận (1)
tìm nghiệm nguyên của pt 2x^2+4y^2+4x+3y-5=0
Cho PT: \(x^2+2x+m-1=0\). Tìm m để PT có 2 nghiệm trái dấu. Khi đó nghiệm nào có giá trị tuyệt đối lớn hơn?
Pt có 2 nghiệm trái dấu khi \(ac< 0\)
\(\Rightarrow1.\left(m-1\right)< 0\Rightarrow m< 1\)
Mặt khác theo Viet: \(x_1+x_2=-2< 0\)
\(\Rightarrow\) Nghiệm âm có giá trị tuyệt đối lớn hơn
Đúng 3
Bình luận (0)




