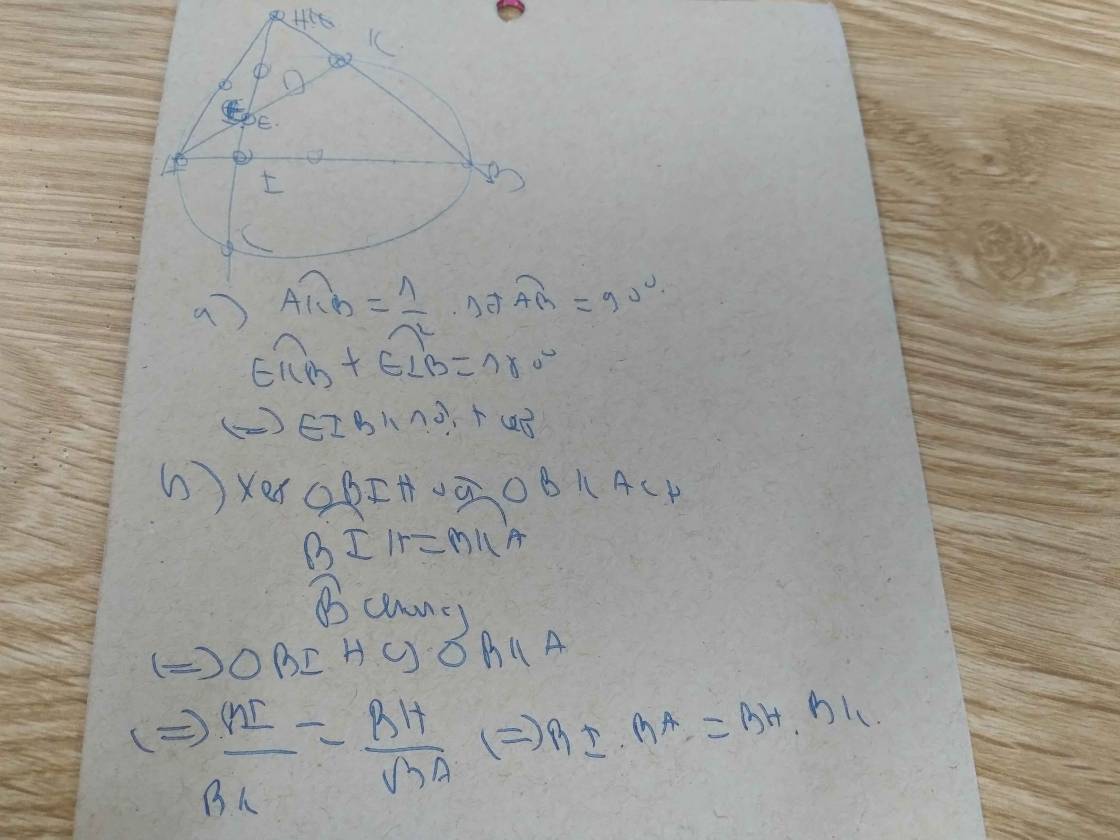Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K. 1.Chứng minh tứ giác BMFE nội tiếp. 2.Chứng minh BF vuông góc với AK và EK.EF = EA.EB 3.Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
QB
Những câu hỏi liên quan
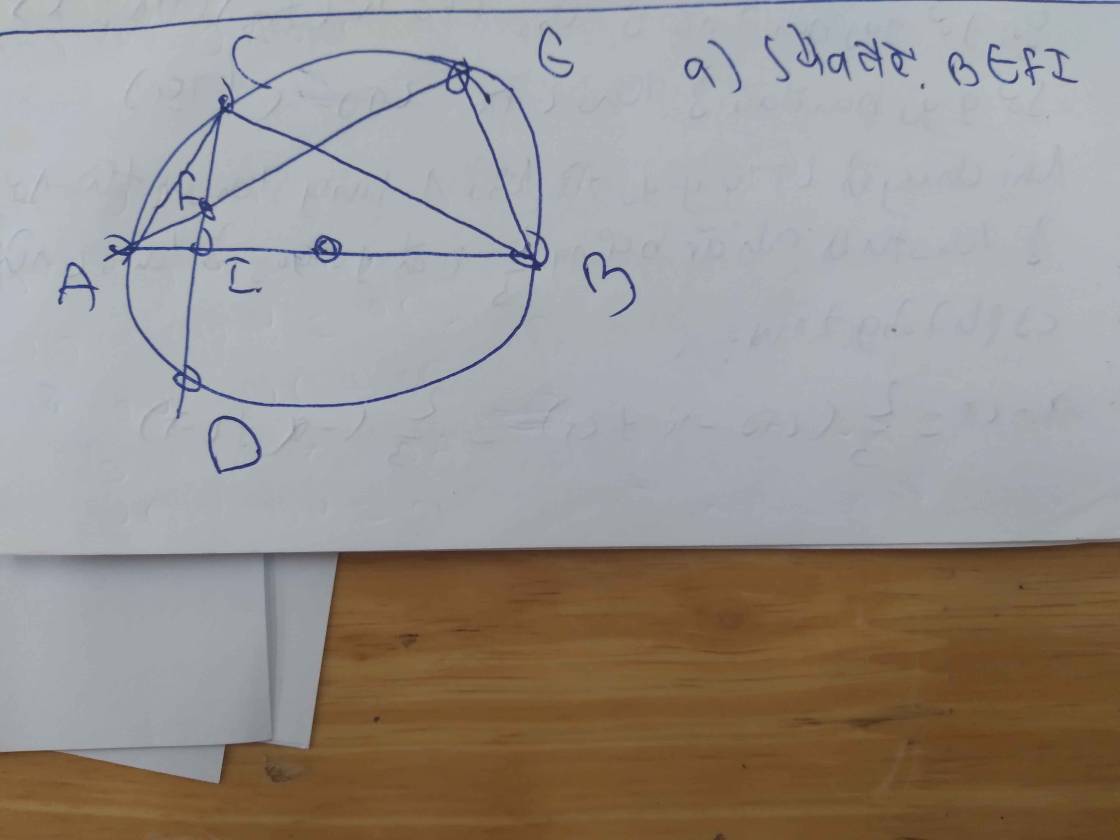
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Xét (O) có
\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AEB}=90^0\)
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{FIB}=180^0\)
nên BEFI là tứ giác nội tiếp
hay B,E,F,I cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
a) \(\Delta ABE\)nội tiếp đường tròn đường kính \(AB\)
\(\Rightarrow\)\(\Delta ABE\perp E\)
\(\Rightarrow\)\(AEB\lambda=90\)độ
Tứ giác\(BEFI\)nội tiếp đường tròn đường kính \(FB\)
cho đường tròn tâm O đường kính AB. vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F chứng minh:
IA.IB=IC.ID VÀ AE.AF=\(AC^2\)(Biết BEFI đã nội tiếp đường tròn)
Xét ΔIAC vuông tại I và ΔIDB vuông tại I có
góc IAC=góc IDB
=>ΔIAC đồng dạng với ΔIDB
=>IA/ID=IC/IB
=>IA*IB=ID*IC
Xét ΔACF và ΔAEC có
góc ACF=góc AEC
góc CAF chung
=>ΔACF đồng dạng với ΔAEC
=>AC/AE=AF/AC
=>AC^2=AE*AF
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB, có H nằm giữa O và A, vẽ dây CD vuông góc OA tại điểm H. Gọi E là điểm đối xứng với A qua H. DE cắt BC tại I. Chứng minh E, I, B nằm trên đg tròn và tìm tâm O'
Cho đường tròn tâm (o) đường kính AB, vẽ dây CD vuông góc với AB tại I ( I nằm giữa AK và B). Trên tia CD lấy điểm H nằm ngoài đường tròn ,HB cắt đường tròn tại K ( K khác B) A cắt CD tại E.
a chứng minh tứ giác BKEI nội tiếp
b chứng minh AB*BI HB* BK
c cho biết AB 8 cm, AK 7 cm.tính diện tích hình quạt tròn BOK ứng với cung nhỏ BK của đường tròn (O) ( kết quả làm tròn đến chữ số thập phân thứ nhất
Đọc tiếp
Cho đường tròn tâm (o) đường kính AB, vẽ dây CD vuông góc với AB tại I ( I nằm giữa AK và B). Trên tia CD lấy điểm H nằm ngoài đường tròn ,HB cắt đường tròn tại K ( K khác B) A cắt CD tại E. a chứng minh tứ giác BKEI nội tiếp b chứng minh AB*BI = HB* BK c cho biết AB= 8 cm, AK = 7 cm.tính diện tích hình quạt tròn BOK ứng với cung nhỏ BK của đường tròn (O) ( kết quả làm tròn đến chữ số thập phân thứ nhất
Cho đường tròn tâm O đường kính AB2R. Vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại Fa) Chứng minh tứ giác BEFL nội tiếp trong một đường trònb) Tính độ dài cạnh AC theo R và góc ACD khi góc BAC60độc) Chứng minh khi điểm E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc một đường thẳng cố định
Đọc tiếp
Cho đường tròn tâm O đường kính AB=2R. Vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại F
a) Chứng minh tứ giác BEFL nội tiếp trong một đường tròn
b) Tính độ dài cạnh AC theo R và góc ACD khi góc BAC=60độ
c) Chứng minh khi điểm E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc một đường thẳng cố định
cho đường tròn tâm o bán kính AB vẽ dây CD vuông góc với AB tại H (H nằm giữa O Và B) tia CD lấy E nằm ngoài đt EB cắt O tại F AF cắt DC tại K a) BFKH là tứ giác nội tiếp b) AB.BH=EB.BF
a: góc AFB=1/2*sđ cung AB=90 độ
góc KHB+góc KFB=90 độ
=>BHKF nội tiếp
b: Xét ΔBHE vuông tại H và ΔBFA vuông tại F có
goc B chung
=>ΔBHE đồng dạng với ΔBFA
=>BH/BF=BE/BA
=>BH*BA=BF*BE
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB . Gọi H là điểm nằm giữa O và B . Kẻ dây CD vuông góc với AB tại H . Trên cung nhỏ AC lấy điểm E , kẻ CK vuông góc với AE tại K . Đường thẳng DE cắt CK tại F . Chứng minh :
a, Tứ giác AHCK nội tiếp đường tròn
b, AH . AD = AD^2
c, Tam giác ACF cân
Cho đường tròn tâm O đường kính AB.Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O).Lấy điểm E trên cung nhỏ BC,E khác B và C,AE cắt CD tại F.
Chứng minh:
a. BEFI là tứ giác nội tiếp đường tròn.
b. AE . AF = AC^2
a) Xét (O): E \(\in\) (O) (gt).
\(\Rightarrow\) \(\widehat{AEB}=90^o\) (Góc nội tiếp).
Xét tứ giác BEFI:
\(\widehat{AEB}+\widehat{CIB}=90^o+90^o=180^o.\)
Mà 2 góc này ở vị trí đối nhau.
\(\Rightarrow\) BEFI là tứ giác nội tiếp đường tròn.
b) Xét (O): \(CD\perp AB\) tại I (gt).
AB là đường kính; CD là dây (gt).
\(\Rightarrow\) I là trung điểm của CD.
Xét tam giác ACD:
AI là đường trung tuyến (I là trung điểm của CD).
AI là đường cao \(\left(AI\perp CD\right).\)
\(\Rightarrow\) Tam giác ACD cân tại A. \(\Rightarrow\) AC = AD (Tính chất tam giác cân).
Xét (O): AC = AD (cmt). \(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}.\)
Xét (O): \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AD}\) (Góc nội tiếp).
Mà \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\) \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AC}.\)
Mà \(\widehat{AEC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
\(\Rightarrow\widehat{ACF}=\widehat{AEC}.\)
Xét tam giác ACF và tam giác AEC:
\(\widehat{A}chung.\)
\(\widehat{ACF}=\widehat{AEC}\left(cmt\right).\)
\(\Rightarrow\) Tam giác ACF \(\sim\) Tam giác AEC (g - g).
\(\Rightarrow\) \(\dfrac{AC}{AE}=\dfrac{AF}{AC}\) (2 cạnh tương ứng tỉ lệ).
\(\Rightarrow AC^2=AE.AF\left(đpcm\right).\)
Đúng 2
Bình luận (0)