Giải giúp m với
ND
Những câu hỏi liên quan
Mn giải giúp mình với ạ:
(X-15) - x.13= 0
Ghi cách giải giúp m với. M cảm ơn ạ.
Lời giải:
$(x-15)-x.13=0$
$x-15-x.13=0$
$(x-x.13)-15=0$
$x(1-13)-15=0$
$x.(-12)-15=0$
$x.(-12)=15$
$x=15:(-12)=\frac{-5}{4}$
Đúng 2
Bình luận (0)
Cho phân số: 1>a/b hãy so sánh a/b với a+m/b+m
Mọi người giải gấp giúp em với ạ ai giải xong trước em tích cho ạ
Mọi người diễn giải ra giúp em vs ạ
ab = a : b
a+m/b+m = (a + m) : (b + m)
a+m/b+m >a /b
Cho phương trình bậc hai x²-2x-m²=0 (*) m là tham số a) Giải phương trình (*) ứng với m=1 b) Với m nào thì phương trình (*) có 2 nghiệm phân biệt Giải giúp em với ạ
a: Khi m=1 thì phương trình sẽ là x^2-2x-1=0
=>x^2-2x+1-2=0
=>(x-1)^2=2
=>\(x=\pm\sqrt{2}+1\)
b: Δ=(-2)^2-4*1*(-m^2)=4m^2+4>=4>0
=>Phương trình luôn có hai nghiệm phân biệt
Đúng 2
Bình luận (0)
giải phương trình x^2 -(m^2 -3m)x+m^3=0 làm ơn giải giúp mình với
Giúp m giải 2 bài này với 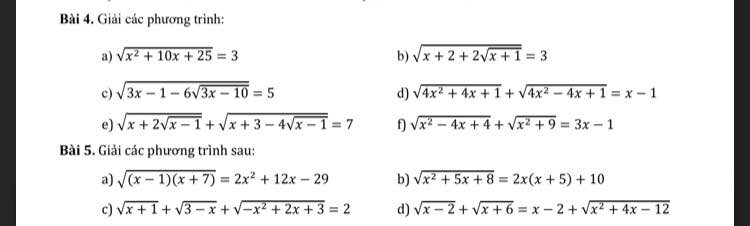
Giúp m giải bài 1,2 với ah!!!!!
1.
\(P=\dfrac{3}{\sqrt{x}+3}\le\dfrac{3}{0+3}=1\)
\(\Rightarrow maxP=1\Leftrightarrow x=0\)
2.
\(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\ge2-\dfrac{3}{0+1}=-1\)
\(\Rightarrow minA=-1\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)
Giải và biện luận các phương trình sau:
a) \(\left(m^2-m-6\right)x=m^2-4x+3\)
b) \(\left|m^2x-1\right|=\left|x+m\right|\)
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP, GIẢI CHI TIẾT GIÚP MÌNH, MÌNH CẢM ƠN
a: Để phương trình có nghiệm duy nhất thì \(\left(m-3\right)\left(m+2\right)< >0\)
hay \(m\notin\left\{3;-2\right\}\)
Để phương trình vô nghiệm thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+2\right)=0\\\left(m-3\right)\left(m-1\right)< >0\end{matrix}\right.\Leftrightarrow m=-2\)
Để phương trình có vô số nghiệm thì m=3
Đúng 0
Bình luận (0)
Giúp mk với
Giải bất phương trình sau với m khác -1
\(\left\{{}\begin{matrix}-1\le\dfrac{m-2}{m+1}\\\dfrac{m-2}{m+1}\le1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le1+\dfrac{m-2}{m+1}\\\dfrac{m-2}{m+1}-1\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le\dfrac{2m-1}{m+1}\\\dfrac{-3}{m+1}\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le\dfrac{2m-1}{m+1}\\m+1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le2m-1\\m+1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{1}{2}\\m>-1\end{matrix}\right.\)\(\Rightarrow m\ge\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
\(-1\le\dfrac{m-2}{m+1}\le1\)
⇔ \(\left|\dfrac{m-2}{m+1}\right|\le1\)
⇔ \(\dfrac{\left(m-2\right)^2}{\left(m+1\right)^2}\le1\)
⇔ \(\left\{{}\begin{matrix}m^2-4m+4\le m^2+2m+1\\m\ne-1\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}m\ge\dfrac{1}{2}\\m\ne-1\end{matrix}\right.\)⇔ m ≥ \(\dfrac{1}{2}\)
Tập nghiệm: \(S=[\dfrac{1}{2};+\infty)\)
Đúng 0
Bình luận (0)
Giải giúp m dạng 1 bài 3,4 với ạ
3: Thay y=4 vào (C), ta được:
\(5x^3-7x^2+8=12x+8\)
\(\Leftrightarrow5x^3-7x^2-12x=0\)
\(\Leftrightarrow x\left(5x^2-7x-12\right)=0\)
\(\Leftrightarrow x\left(5x-12\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{12}{5}\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)




