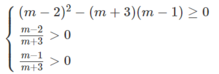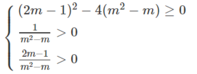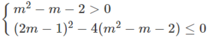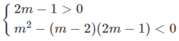\(\left\{{}\begin{matrix}-1\le\dfrac{m-2}{m+1}\\\dfrac{m-2}{m+1}\le1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le1+\dfrac{m-2}{m+1}\\\dfrac{m-2}{m+1}-1\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le\dfrac{2m-1}{m+1}\\\dfrac{-3}{m+1}\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le\dfrac{2m-1}{m+1}\\m+1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}0\le2m-1\\m+1>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{1}{2}\\m>-1\end{matrix}\right.\)\(\Rightarrow m\ge\dfrac{1}{2}\)
\(-1\le\dfrac{m-2}{m+1}\le1\)
⇔ \(\left|\dfrac{m-2}{m+1}\right|\le1\)
⇔ \(\dfrac{\left(m-2\right)^2}{\left(m+1\right)^2}\le1\)
⇔ \(\left\{{}\begin{matrix}m^2-4m+4\le m^2+2m+1\\m\ne-1\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}m\ge\dfrac{1}{2}\\m\ne-1\end{matrix}\right.\)⇔ m ≥ \(\dfrac{1}{2}\)
Tập nghiệm: \(S=[\dfrac{1}{2};+\infty)\)