GIÚP EM VÓI Ạ,EM CẦN GẤPPPPPP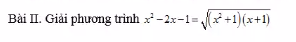
TM
Những câu hỏi liên quan
 giúp em bài 1 dạng 3 vói em, em cần gấp lắm, em cảm ơn ạ
giúp em bài 1 dạng 3 vói em, em cần gấp lắm, em cảm ơn ạ
Bài 1:
1) \(\Rightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
2) \(\Rightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
3) \(\Rightarrow\left(4x-3\right)\left(7-12x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{7}{12}\end{matrix}\right.\)
4) \(\Rightarrow x^3+8-x^3+25x=-17\)
\(\Rightarrow25x=-25\Rightarrow x=-1\)
5) \(\Rightarrow\left(3x-2\right)\left(3x+2\right)-2\left(3x-2\right)^2=0\)
\(\Rightarrow\left(3x-2\right)\left(3x+2-6x+4\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(-3x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 3:
c: \(x^2+7x+12=\left(x+3\right)\left(x+4\right)\)
d: \(x^3-7x-6\)
\(=x\left(x-1\right)\left(x+1\right)-6\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x-6\right)\)
\(=\left(x+1\right)\left(x-3\right)\left(x+2\right)\)
Đúng 0
Bình luận (0)
GIÚP EM CÂU C BÀI 2 VÓI ẠAAA,EM CẦN GẤP LẮM RỒI Ạ
1) Theo em, người tự lập có cần lời khuyên từ người khác hay không ? Vì sao ? 2) Nêu 4 ví dụ về sự sáng tạo trong lao động, trong học tập GIÚP MÌNH VỚI Ạ . MÌNH SẮP THI RỒI NÊN CẦN GẤPPPPPP
Giúp em vói ạ😢
Mn giúp em vói ạ
giúp em câu 8,9 vói ạ
làm giúp em này vói ạ
R=1/2CD=a
h=AD=2a
S1=Sxq=2*pi*r*h=2*pi*a*2a=4*pi*a^2
S2=Stp=2*pi*r^2+2*pi*r*h
=2*pi*a^2+2*pi*a*2a
=6*pi*a^2
>S1/S2=2/3
Đúng 0
Bình luận (0)
xin mọi người giúp em vói ạ
13.
\(\lim\limits_{x\rightarrow1}\left(3x^2-2x-1\right)=3.1^2-2.1-1=0\)
14.
\(\lim\limits_{x\rightarrow9}\sqrt{x+16}=\sqrt{9+16}=5\)
15.
\(\lim\limits_{x\rightarrow+\infty}x^{2021}=+\infty\)
16.
\(\lim\limits_{x\rightarrow-\infty}\left(x-x^3+1\right)=\lim\limits_{x\rightarrow-\infty}x^3\left(-1+\dfrac{1}{x^2}+\dfrac{1}{x^3}\right)\)
Do \(\lim\limits_{x\rightarrow-\infty}x^3=-\infty\)
\(\lim\limits_{x\rightarrow-\infty}\left(-1+\dfrac{1}{x^2}+\dfrac{1}{x^3}\right)=-1< 0\)
\(\Rightarrow\lim\limits_{x\rightarrow-\infty}x^3\left(-1+\dfrac{1}{x^2}+\dfrac{1}{x^3}\right)=+\infty\)
Đúng 0
Bình luận (0)
17.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2x^2+5x-3}{x^2+6x+3}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(2+\dfrac{5}{x}-\dfrac{3}{x^2}\right)}{x^2\left(1+\dfrac{6}{x}+\dfrac{3}{x^2}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{2+\dfrac{5}{x}-\dfrac{3}{x^2}}{1+\dfrac{6}{x}+\dfrac{3}{x^2}}=\dfrac{2+0-0}{1+0+0}=2\)
18.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{4x^2-x-1}}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left|x\right|\sqrt{4-\dfrac{1}{x}-\dfrac{1}{x^2}}}{x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-x\sqrt{4-\dfrac{1}{x}-\dfrac{1}{x^2}}}{x\left(1+\dfrac{1}{x}\right)}=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{4-\dfrac{1}{x}-\dfrac{1}{x^2}}}{1+\dfrac{1}{x}}\)
\(=\dfrac{-\sqrt{4}}{1}=-2\)
Đúng 0
Bình luận (0)
19.
\(\lim\limits_{x\rightarrow-\infty}\left(2x^3-x^2\right)=\lim\limits_{x\rightarrow-\infty}x^3\left(2-\dfrac{1}{x}\right)\)
Do \(\lim\limits_{x\rightarrow-\infty}x^3=-\infty\)
\(\lim\limits_{x\rightarrow-\infty}\left(2-\dfrac{1}{x}\right)=2>0\)
\(\Rightarrow\lim\limits_{x\rightarrow-\infty}x^3\left(2-\dfrac{1}{x}\right)=-\infty\)
20.
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+1}-x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(\sqrt{x^2+1}-x\right)\left(\sqrt{x^2+1}+x\right)}{\sqrt{x^2+1}+x}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{1}{\sqrt{x^2+1}+x}=\lim\limits_{x\rightarrow+\infty}\dfrac{x\left(\dfrac{1}{x}\right)}{x\left(\sqrt{1+\dfrac{1}{x^2}}+1\right)}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{1}{x}}{\sqrt{1+\dfrac{1}{x^2}}+1}=\dfrac{0}{1+1}=0\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
làm giúp em bài này vói ạ
\(S_{Xq}=2\cdot pi\cdot2^2+\dfrac{1}{2}\cdot\sqrt{5}\cdot2=3\sqrt{5}\cdot pi\)
Đúng 0
Bình luận (0)



