giúp minh câu 1 abc với câu 2 ab với mình cảm ơn
NK
Những câu hỏi liên quan
câu 1: cho tam giác ABC vuông tại A. Tia phân giác của góc ACB cắt AB ở D. Vẽ DE vuông góc với BC tại E. Chứng minh rằng DA=DE
giúp mình với, mình đang cần gấp, cảm ơn
xét tam giác ADC vuông tại A( tam giác ABC vuông tại A) và tam giác CDE vuông tại E( DE vuông góc với BC) có:
EDC=DCA ( CD là tia phân giác góc ACB) và CD là cạnh chung
=> tam giác ACD=tam giác ECD( ch-gn)
=>DE=DA( cặp cạnh tương ứng)
Câu 1: Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho góc ABD = góc ACB
a) Chứng minh: Tam giác ABD đồng dạng với tam giác ACB và viết tỉ số đồng dạng
b) Chứng minh: AB2 = AD . AC
- Giúp mình với nhé, mình cảm ơn nhiều
Cho tam giác ABC vuông tại A, đường phân giác AD. Chứng minh rằng √2/AD = 1/AB + 1/AC. Kẻ đường cao AH và đường trung tuyến AM của tam giác ABC chứng minh rằng nếu 1/ah^2+1/am^2=2/ad^2. Giúp mình câu 2 thôi ạ mình cảm ơn
Để chứng minh rằng √2/AD = 1/AB + 1/AC, ta có thể sử dụng định lý phân giác trong tam giác vuông.
Vì tam giác ABC vuông tại A, nên ta có đường phân giác AD chia góc BAC thành hai góc bằng nhau.
Áp dụng định lý phân giác, ta có:
AB/BD = AC/CD
Từ đó, ta có:
AB/AD + AC/AD = AB/BD + AC/CD
= (AB + AC)/(BD + CD)
= (AB + AC)/BC
= 1/BC (vì tam giác ABC vuông tại A)
Vậy, ta có:
1/AD = 1/AB + 1/AC
√2/AD = √2/AB + √2/AC
Vậy, chứng minh đã được hoàn thành.
Để chứng minh rằng nếu 1/ah^2 + 1/am^2 = 2/ad^2, ta cần có thông tin chi tiết về tam giác ABC và các điều kiện đi kèm.
Đúng 0
Bình luận (0)
2/AD^2=(căn 2/AD)^2
=(1/AB+1/AC)^2
\(=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}+2\cdot\dfrac{1}{AB\cdot AC}\)
\(=\dfrac{1}{AH^2}+2\cdot\dfrac{1}{AH\cdot BC}\)
\(=\dfrac{1}{AH^2}+\dfrac{1}{AM^2}\)
Đúng 0
Bình luận (0)
ai giúp mình với minh cảm ơn nhìu ạ. làm câu nào nào cũng được ạ mình cảm ơn 
Giúp mình giải các câu này với mình cảm ơn các bạn nhiều ^^ Câu 1: Thực hiện phép trừ 3/2x+6 - x-6/2x^2+6x Câu 2: Với giá trị nào của x thì giá trị của phân thức 7x/x-2 được xác định Câu 3: Tứ giác ABCD có Â110 độ,B 120 độ,D75 độ tính số đo góc C Câu 4: cho tam giác ABC cân tại A đường cao AH trên cạnh AB lấy điểm I,trên cạnh AC lấy điểm K sao cho AIAK chứng minh rằng điểm I đối xứng với điểm K qua AH
Đọc tiếp
Giúp mình giải các câu này với mình cảm ơn các bạn nhiều ^^ Câu 1: Thực hiện phép trừ 3/2x+6 - x-6/2x^2+6x Câu 2: Với giá trị nào của x thì giá trị của phân thức 7x/x-2 được xác định Câu 3: Tứ giác ABCD có Â=110 độ,B= 120 độ,D=75 độ tính số đo góc C Câu 4: cho tam giác ABC cân tại A đường cao AH trên cạnh AB lấy điểm I,trên cạnh AC lấy điểm K sao cho AI=AK chứng minh rằng điểm I đối xứng với điểm K qua AH
Giúp mình câu 1 và 2 với ạ. Mình cảm ơn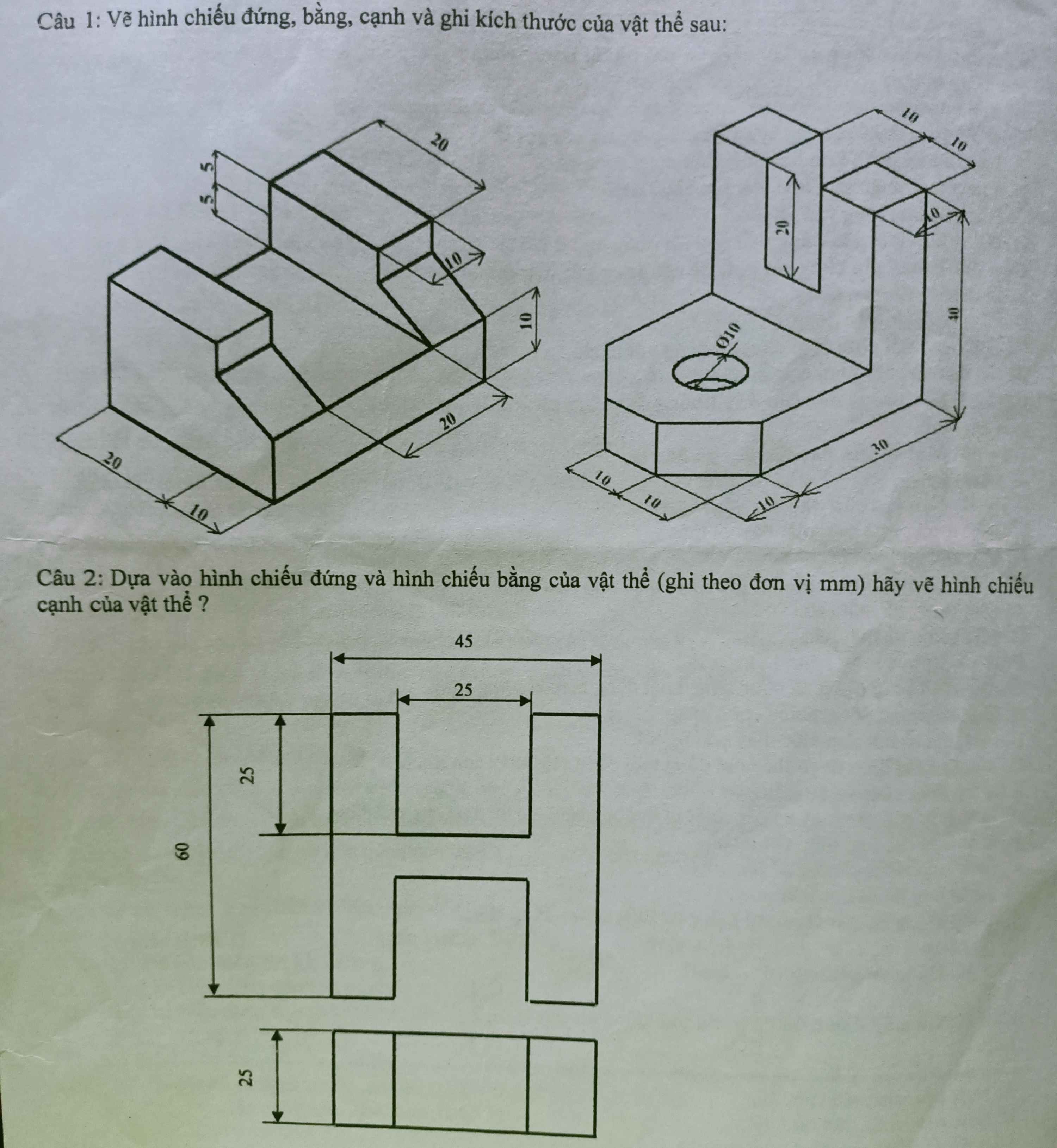
Cho hình thang ABCD , biết góc A = góc B =90 dộ , AB=BC=1/2AD
câu a : tính các góc của hình thang
Câu b : chứng minh AC vuông góc với CD
câu c: tính chu vi hình thang nếu AB =3cm
Ai giúp mình với được không ạ <3 mình cảm ơn nhiều ạ
Cho hình thang ABCD , biết góc A = góc B =90 dộ , AB=BC=1/2AD
câu a : tính các góc của hình thang
Câu b : chứng minh AC vuông góc với CD
câu c: tính chu vi hình thang nếu AB =3cm
Ai giúp mình với được không ạ <3 mình cảm ơn nhiều ạ
Chào cả nhà, giải hộ giúp mình câu c nhé. Cảm ơn nhiều.
Bài 6: Cho tam giác ABC cân tại A , Từ B kẻ đường thẳng vuông góc với AB, từ C kẻ đường thẳng vuông góc với AC , hai đường thẳng này cắt nhau tại M.
a) Chứng minh ∆MAB = ∆MAC
b)Chứng minh ∆ MBC là tam giác đều.
c) Gọi H là giao điểm của AM và BC . Chứng minh BH + AM > AB + BM.