trong mặt phẳng tọa độ hãy vẽ đường thẵng đi qua 2 điểm O(0;0) và A(1;2) .đường thẳng OA là đồ thị của hàm số nào ?
VD
Những câu hỏi liên quan
Trong mặt phẳng tọa độ hãy vẽ đường thẳng đi qua hai điểm O(0;0) và A(1;2). Đường thẳng OA là đồ thị của hàm số nào?
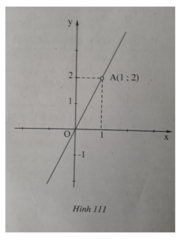
Trước hết hãy xác định các điểm O và A. O chính là gốc tọa độ. A là điểm có hoành độ là 1 và tung độ là 2. Xem hình 111.
+)Vì đường thẳng OA đi qua gốc tọa độ O nên OA là đồ thị của hàm số y = ax (a ≠ 0)
+) Vì đồ thị đi qua A(1; 2) nên thay x = 1; y = 2 vào ta được:
2 = a.1 ⇔ a = 2
+) Vậy đường thẳng OA là đồ thị của hàm số y = 2x.
Đúng 1
Bình luận (0)
vẽ hệ trục tọa độ Oxy. Biểu diễn các điểm A(1,-3), B(-1,3) trên mặt phẳng tọa độ
vẽ đường thẳng đi qua 2 điểm A và B. Em có nhận xét gì về đường thẳng AB với gốc tọa độ O
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A (-1;1) và đường thẳng
d : x - y + 1 - √2 = 0 . Viết phương trình đường tròn (C) đi qua điểm A, gốc toạ độ O và tiếp xúc với đường thẳng d .
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A (-1;1) và đường thẳng
d : x - y + 1 - √2 = 0 . Viết phương trình đường tròn (C) đi qua điểm A, gốc toạ độ O và tiếp xúc với đường thẳng d .
Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho 2 điểm A( 1;2) B (3;4) và đường thẳng (d): 3x+y-3=0
a) gọi (C1) (C2) là 2 đường tròn cùng đi qua qua 2 điểm A, B và tiếp xúc với (O). Lập phương trình của 2 đường tròn trên
b) Tìm tọa độ của điểm M trên (d) sao cho từ đó vẽ được 1 tiếp tuyến chung (d) # (d) của đường tròn (C1) và (C2)
Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ của K.
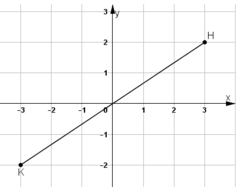
K đối xứng với H qua gốc tọa độ ⇔ O(0; 0) là trung điểm của KH.
Dựa vào hình biểu diễn ta có K(-3; -2).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B.
36
2
π
C.
18
2
π
D. 18π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B.
36
2
π
C. 18 2 π
D. 18π
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;1;-2) và B(0;-2;3). Mặt phẳng (P) đi qua gốc tọa độ và vuông góc với đường thẳng đi qua hai điểm A, B có phương trình là A. x - 2y + z 0. B. x - y + z 0. C. x + y - 3z 0. D. x + 3y - 5z 0.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;1;-2) và B(0;-2;3). Mặt phẳng (P) đi qua gốc tọa độ và vuông góc với đường thẳng đi qua hai điểm A, B có phương trình là
A. x - 2y + z = 0.
B. x - y + z = 0.
C. x + y - 3z = 0.
D. x + 3y - 5z = 0.
Chọn D.
Ta có (P) qua O(0;0;0) và nhận BA → = ( 1 ; 3 ; - 5 ) là một VTPT
⇒ ( P ) : x + 3 y - 5 z = 0 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ của K ?
51. Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ K.
Bài giải:
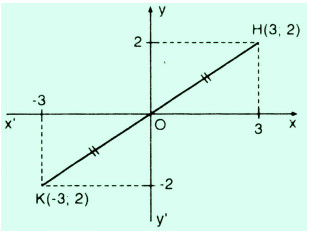
Trên mặt phẳng tọa độ xOy, xác định điểm H có tọa độ (3 ; 2). Như vậy ta đã có hai điểm O và H. Để vẽ điểm K đối xứng với điểm H qua gốc tọa độ, ta vẽ một đường thẳng đi qua hai điểm O và H, rồi lấy điểm K thuộc OH sao cho O là trung điểm của đoạn KH.
Khi đó điểm K có tọa độ (-3 ; -2).
Đúng 0
Bình luận (0)



