giải bất phương trình
6x^3-x^2+13x-10<0
VQ
Những câu hỏi liên quan
giải phương trình
6x^2 + x=0
`6x^2+x=0`
`<=>x(6x+1)=0`
`<=>` \(\left[ \begin{array}{l}x=0\\6x=-1\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}x=0\\x=-\dfrac16\end{array} \right.\)
Vậy `S={0;-1/6}`
Đúng 2
Bình luận (0)
Ta có: \(6x^2+x=0\)
\(\Leftrightarrow x\left(6x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{6}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải bất phương trình \(\dfrac{x^2-13x+2}{x^2+5}\le-2\)
=>\(\dfrac{x^2-13x+2+2x^2+10}{x^2+5}< =0\)
=>3x^2-13x+12<=0
=>4/3<=x<=3
Đúng 0
Bình luận (0)
- giải các bất phương trình sau:
a) (\(3x^2-7x+4\))(\(x^2+x+4\))\(>0\)
b) \(x^3-13x^2+42x-36>0\)
c) \(x\left(x+5\right)\le2\left(x^2+2\right)\)
a: =>(x-1)(3x-4)>0
=>x>4/3 hoặc x<1
b: =>x^3-3x^2-10x^2+30x+12x-36>0
=>(x-3)(x^2-10x+12)>0
Th1: x-3>0và x^2-10x+12>0
=>x>5+căn 13
TH2: x-3<0 và x^2-10x+12<0
=>x<3 và 5-căn 13<x<5+căn 13
=>3<x<5+căn 13
Đúng 0
Bình luận (0)
Giải các bất phương trình sau bằng 1 3 x ≥ x + 1
Vẽ đồ thị của hàm số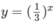 
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
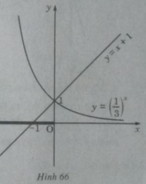
Khi x < 0 đồ thị của hàm số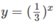 
nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-
∞
;0]
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
1
3
x
+
2
3
−
x
A.
0
;
2
.
B.
2
;
+
∞
.
C. ...
Đọc tiếp
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x
A. 0 ; 2 .
B. 2 ; + ∞ .
C. − 2 ; − 1 .
D. 0 ; + ∞ .
Tập nghiệm của bất phương trình
1
3
x
+
2
3
-
x
Đọc tiếp
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x
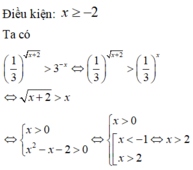
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là S = 2 ; + ∞
Đáp án A
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
1
3
x
+
2
3
-
x
A.
2
;
+
∞
B.
1
;
2...
Đọc tiếp
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x
A. 2 ; + ∞
B. 1 ; 2
C. ( 1 ; 2 ]
D. [ 2 ; + ∞ )
Tập nghiệm của bất phương trình
1
3
x
+
2
3
-
x
là A.
1
,
2
. B.
2
,
+
∞...
Đọc tiếp
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x là
A. 1 , 2 .
B. 2 , + ∞ .
C. [ 2 , + ∞ ) .
D. ( 1 , 2 ]
Tập nghiệm của bất phương trình
1
3
x
+
2
3
−
x
là A. (1;2) B.
2
,
+
∞
.
C.
2
,
+...
Đọc tiếp
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x là
A. (1;2)
B. 2 , + ∞ .
C. 2 , + ∞ .
D. 1 , 2 .
