Hình vẽ đâu rồi bạn?

Bạn cho mình hỏi chỗ :2√2 là j ạ

a) Ta có: \(\left(2\sqrt{2}\right)^2=8\)

\(2^2+2^2=4+4=8\)

Do đó: \(\left(2\sqrt{2}\right)^2=2^2+2^2\)(=8)

hay \(2\sqrt{2}\)cm; 2cm; 2cm là số đo ba cạnh của một tam giác vuông 

b) Ta có: \(17^2=289\)

\(8^2+15^2=64+225=289\)

Do đó: \(17^2=8^2+15^2\)(=289)

hay 17cm; 8cm và 15cm là số đo ba cạnh của một tam giác vuông

c) Ta có: \(25^2=625\)

\(7^2+24^2=49+576=625\)

Do đó: \(25^2=7^2+24^2\)(=625)

hay 25cm; 7cm và 24cm là số đo ba cạnh của một tam giác vuông

d) Ta có: \(10^2=100\)

\(6^2+8^2=36+64=100\)

Do đó: \(10^2=6^2+8^2\)(=100)

hay 10cm; 6cm và 8cm là số đo ba cạnh của một tam giác vuông

e) Ta có: \(11^2=121\)

\(6^2+9^2=36+81=117\)

Do đó: \(11^2\ne6^2+9^2\)(\(121\ne117\))

hay 11cm; 6cm và 9cm không là số đo ba cạnh của một tam giác vuông

f) Ta có: \(\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)

\(1^2+1^2=1+1=2=\dfrac{8}{4}\)

Do đó: \(\left(\dfrac{3}{2}\right)^2\ne1^2+1^2\left(\dfrac{9}{4}\ne\dfrac{8}{4}\right)\)

hay \(\dfrac{3}{2}cm\); 1cm và 1cm không là số đo ba cạnh của một tam giác vuông

GIÚP E VỚI Ạ E CẢM ƠN 

\(S_{hình.thoi}=\dfrac{1}{2}\cdot15\cdot6=45\left(cm^2\right)\\ S_{mảnh.đất}=\dfrac{1}{2}\cdot24\cdot2\cdot24=576\left(cm^2\right)\)

Đường chéo lớn là \(\left(30+2\right):2=16\left(cm\right)\)

Đường chéo bé là \(30-16=14\left(cm\right)\)

\(\Rightarrow S_{hình.thoi}\left(2\right)=\dfrac{1}{2}\cdot16\cdot14=112\left(cm^2\right)\)

Giúp tao bài này

vì diện tích của tam giác ABC là `15cm^2`

diện tích của tam giác DEF là: `60cm^2`

mà tam giác ABC đồng dạng tam giác DEF 

Suy ra tam giác ABC đồng dạng tam giác DEF theo tỉ số đồng dạng

\(k=\sqrt{\dfrac{15}{60}}=\dfrac{1}{2}\left(đl\right)\)

\(=>\dfrac{BC}{EF}=\dfrac{1}{2}\\ =>\dfrac{10}{EF}=\dfrac{1}{2}\\ =>EF=20\left(cm\right)\)

A.

A

A

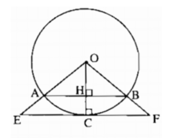
Gọi C là tiếp điểm của EF với đường tròn (O), H là giao điểm của OC và AB. Ta có OC ⊥ EF và AB // EF nên OC ⊥ AB.

Ta tính được HB = 12 cm nên OH = 9 cm.

Ta tính được EF = 40cm.