Cho x>y>2
a.chứng minh x+y>4, xy>4
b. x2 -xy>0, y2 -2y>0, xy-y2>0
cho x≠0, y≠0 thỏa mãn: (x+y)xy=x2+y2-xy. Tính max A=\(\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y}\). khi đó gt trở thành:
\(a+b=a^2+b^2-ab\ge\dfrac{1}{4}\left(a+b\right)^2\Leftrightarrow o\le a+b\le4\);
\(A=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=\left(a+b\right)^2\le16\)
Đẳng thức xảy ra khi và chỉ khi a=b=2 <=> x=y=1/2
Vậy Max A = 16
Cho x, y là hai số thực thỏa mãn x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1. Chứng minh rằng x 1 + y 2 + y 1 + x 2 = 0.
x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1 ⇔ ( 1 + x ) 2 ( 1 + y ) 2 = 1 − x y ⇒ ( 1 + x 2 ) ( 1 + y 2 ) = 1 - x y 2 ⇔ 1 + x 2 + y 2 + x 2 y 2 = 1 − 2 x y + x 2 y 2 ⇔ x 2 + y 2 + 2 x y = 0 ⇔ x + y 2 = 0 ⇔ y = − x ⇒ x 1 + y 2 + y 1 + x 2 = x 1 + x 2 − x 1 + x 2 = 0
Cho x,y >0 và X2 +y2 =8 . Tìm GTLN của xy/xy+1 .
Đặt \(P=\dfrac{xy}{xy+1}\Rightarrow\dfrac{1}{P}=\dfrac{xy+1}{xy}=1+\dfrac{1}{xy}\)
Ta có : \(xy\le\dfrac{x^2+y^2}{2}=\dfrac{8}{2}=4\Rightarrow\dfrac{1}{xy}\ge4\)
\(\Rightarrow\dfrac{1}{P}\ge5\Rightarrow P\le\dfrac{1}{5}\)
Dấu "=" xảy ra khi $x=y=2$
chứng minh rằng: 1x+1y≤−2 biết x3+y3+3(x2+y2)+4(x+y)+4=0 và xy>0
CMR: \(\frac{1}{x}+\frac{1}{y}\le2\) biết \(^{x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0}\) và xy>0
Cho x,y khác 0 và (x+y)xy=x2+y2-xy
Tìm Max P=\(\dfrac{1}{x^3}\) + \(\dfrac{1}{y^3}\)
\(P=\dfrac{x^3+y^3}{x^3y^3}=\dfrac{\left(x+y\right)\left(x^2+y^2-xy\right)}{x^3y^3}=\dfrac{x^2y^2\left(x+y\right)}{x^3y^3}=\dfrac{x+y}{xy}=\dfrac{\left(x+y\right)^2}{xy\left(x+y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{x^2+y^2-xy}=\dfrac{4\left(x^2+y^2-xy\right)-3\left(x^2+y^2-2xy\right)}{x^2+y^2-xy}\)
\(=4-\dfrac{3\left(x-y\right)^2}{x^2+y^2-xy}\le4\)
\(P_{max}=4\) khi \(x=y=\dfrac{1}{2}\)
Cho x2 + y2 = 1
Giải : \(2\sqrt{3}x+4\sqrt{3}xy+4y^2-2y-5=0\)
Cho mình hỏi là nếu như mình đặt x = sina và y = cosa
Cho x > 0 và số thực y thỏa mãn 2 x + 1 x = log 2 14 - y - 2 y + 1 . Giá trị của biểu thức P = x 2 + y 2 - x y + 1 bằng
A. 1
B. 2
C. 3
D. 4
Cho hai số thực x≠0, y≠0 thay đổi và thỏa mãn điều kiện (x+y).xy=x2+y2–xy. Giá trị lớn nhất của biểu thức M = 1 x 3 + 1 y 3 là
A. 18
B. 1
C. 9
D. 16
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được : 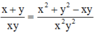
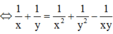
Đặt 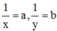 ta có
ta có ![]()
Khi đó ![]()
![]()
Ta có ![]() mà
mà 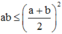
nên ![]()
![]()
![]()
Dấu đẳng thức xảy ra khi 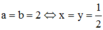 . Vậy Mmax = 16
. Vậy Mmax = 16
cho x,y là 2 số thực ≠0 thỏa mãn 2x2+ y2/4 +1/x2=4
A=2018+xy