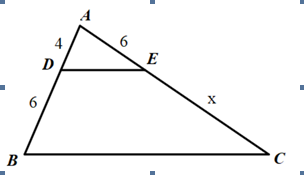
Cho hình vẽ, biết ΔABC có DE=BC , AB = 4cm , DB = 6cm AE = 6cm . Tìm x
Cho ΔABC có đường phân giác AD (D∈BC). Biết AB=4cm, AC= 6cm, DB=3cm. Tính DC,BC
GIÚP MIK VS
xét ΔABC có AD là đường phân giác
=>\(\dfrac{AB}{BD}=\dfrac{AC}{DC}hay\dfrac{4}{3}=\dfrac{6}{DC}\)
=>DC=\(\dfrac{6.3}{4}=4,5\left(cm\right)\)
BC=BD+DC
=3+4,5
BC=7,5cm
Cho ΔABC cân tại A. Vẽ phân giác BD,CE.
a) Chứng minh: BD=CE
b) Chứng minh DE=BC
c) Biết AB=AC=6cm, BC=4cm. Tính AD, DC
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Cho ΔABC cân tại A có AB=AC=6cm, BC=4cm. Tính bán kính đường tròn tìm ngoại tiếp ΔABC
Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)
cho ΔABC vuông tại A có AB=6cm, AC=8cm. AD là tia phân giác của ∠BAC( D∈BC)
a) tính tỉ số \(\dfrac{BD}{DC}\)và độ dài đoạn thẳng BC, DB, DC
b) kẻ DE⊥AB. Tính độ dài DE, AE và diện tích tứ giác AEDC
c) gọi O là giao điểm AD và CE. Qua O kẻ đg thẳng // AC cắt BC và AB lần lượt tại M, N. C/m: OM=ON
a: BC=10cm
Xét ΔABC có AD là phân giác
nên BD/CD=AB/AC=3/4
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó: BD=30/7(cm); CD=40/7(cm)
b: Xét ΔABC có DE//AC
nên DE/AC=BD/BC
=>\(\dfrac{DE}{8}=\dfrac{30}{7}:10=\dfrac{3}{7}\)
=>DE=24/7(cm)
Cho ΔABC có AB = 5 cm, AC =7,5cm, BC =6cm. Trên AB, AC lấy điểm D,E sao cho AD= 3cm, AE =2cm
a) Chứng minh ΔADE ~ ΔACB
b) Tính DE
Cho ΔABC vuông tại A, BD là tia p/g của góc ABD(D∈AC). DE⊥BC tại E. AB cắt DE tại K.
a, ΔBAE cân
b, Biết AD=6CM. AC=16cm. EC=?
C, AE//CK
a.Xét ΔABD và ΔIBD có:
BAD=BID=90 độ
BD chung
ABD=IBD (do BD là phân giác góc ABC)
=>ΔABD=ΔIBD (ch-gn)
b.Ta có: ΔABD=ΔIBD (cm câu a)
=>AB=IB (2 cạnh tương ứng)
=>ΔABI cân tại B
Lại có: BD là đường phân giác góc B
=>BD đồng thời là đường cao
=>BD⊥AI
c.Ta có: ΔABD=ΔIBD (cm câu a)
=>AD=ID (2 cạnh tương ứng)
Xét ΔDAK và ΔDIC có:
DAK=DIC (=90 độ)
DA=DI (cmt)
ADK=IDC (2 góc đối đỉnh)
=>ΔDAK=ΔDIC (g.c.g)
=>DK=DC (2 cạnh tương ứng)
d.Vì ΔABC vuông tại A nên:
=>BC²=AB²+AC²
<=>BC²=6²+8²
<=>BC²=100
<=>BC=√100=10 (cm)
Ta có: BI+IC=BC
=>IC=BC-BI
Lại có: AB=BI (cm câu b)
=>IC=BC-AB
=>IC=10-6=4 (cm)
Vậy IC=4 cm.
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
Suy ra: BA=BE(hai cạnh tương ứng)
Xét ΔBAE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
a) Xét ∆ABD và ∆EBD:
BD cạnh chung
\(\widehat{BAD}=\widehat{BED}=90^o\)
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> ∆ABD=∆EBD (ch.gn)
=> AB=BE (2 cạnh t/ứ)
=> ∆ABE cân tại A
b) Ta có: DC=AC-AD=16-6=10 (cm)
Theo câu a: ∆ABD=∆EBD
=> AD=ED=6
Áp dụng định lý Py-ta-go vào tam giác EDC vuông tại E, ta có:
\(DC^2=EC^2+DE^2\)
\(\Leftrightarrow10^2=6^2+EC^2\Rightarrow EC^2=10^2-6^2=64=8^2\)
\(\Rightarrow EC=8\left(cm\right)\)
c) Xét ∆ADK và ∆EDC:
AD=ED(cm ở b)
\(\widehat{ADK}=\widehat{EDC}\) (2 góc đối đỉnh)
\(\widehat{DAK}=\widehat{DEC}=90^o\)
=> ∆ADK=∆EDC (g.c.g)
=> AK=EC (2 cạnh t/ứ)
Mà AB=BE (cm ở a)
=> AK+AB=EC+BE
<=> BK=BC
=> ∆BCK cân ở B
Theo câu a: ∆ABE cân ở B
=> \(\widehat{BAE}=\dfrac{180^o-\widehat{B}}{2}\)
Lại có ∆BKC cân ở B(cmt)
=> \(\widehat{BKC}=\dfrac{180^o-\widehat{B}}{2}\)
=> \(\widehat{BAE}=\widehat{BKC}\)
Mà 2 góc này ở vị trí đồng vị
=> AE//KC
Cho tam giác \(ABC\), biết \(DE//BC\) và \(AE = 6cm,EC = 3cm,DB = 2cm\) (Hình 1). Độ dài đoạn thẳng \(AD\) là
A. 4cm.
B. 3 cm.
C. 5cm.
D. 3,5 cm.
Xét tam giác \(ABC\) có \(DE//BC\) nên theo định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{x}{2} = \frac{6}{3}\). Do đó, \(x = \frac{{6.2}}{3} = 4\).
Vậy \(x = 4\).
Cho ΔABC có AB = 4cm, AC= 6cm, BC= \(2\sqrt{13}\) cm.
Chứng minh : AB.sinB = AC. SinC
Ta có:
\(AB^2=4^2=16\)
\(AC^2=6^2=36\)
\(BC^2=\left(2\sqrt{13}\right)^2=52\)
\(\Rightarrow AB^2+AC^2=BC^2\left(=52\right)\)
\(\Rightarrow\Delta ABC\) vuông tại A (theo định lý Pytago đảo)
\(\Rightarrow sinB=\dfrac{AC}{BC}\)
\(sinC=\dfrac{AB}{BC}\)
\(\Rightarrow\dfrac{sinB}{sinC}=\dfrac{\dfrac{AC}{BC}}{\dfrac{AB}{BC}}=\dfrac{AC}{AB}\)
\(\Rightarrow AB.sinB=AC.sinC\)