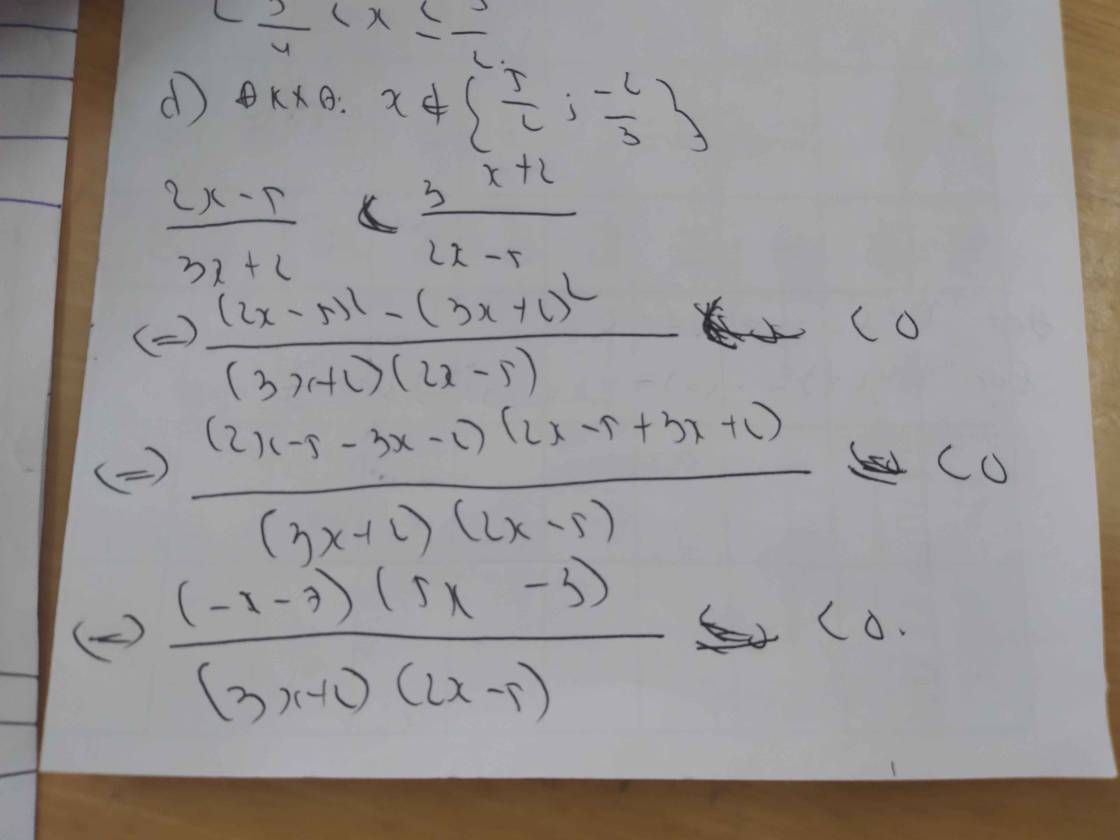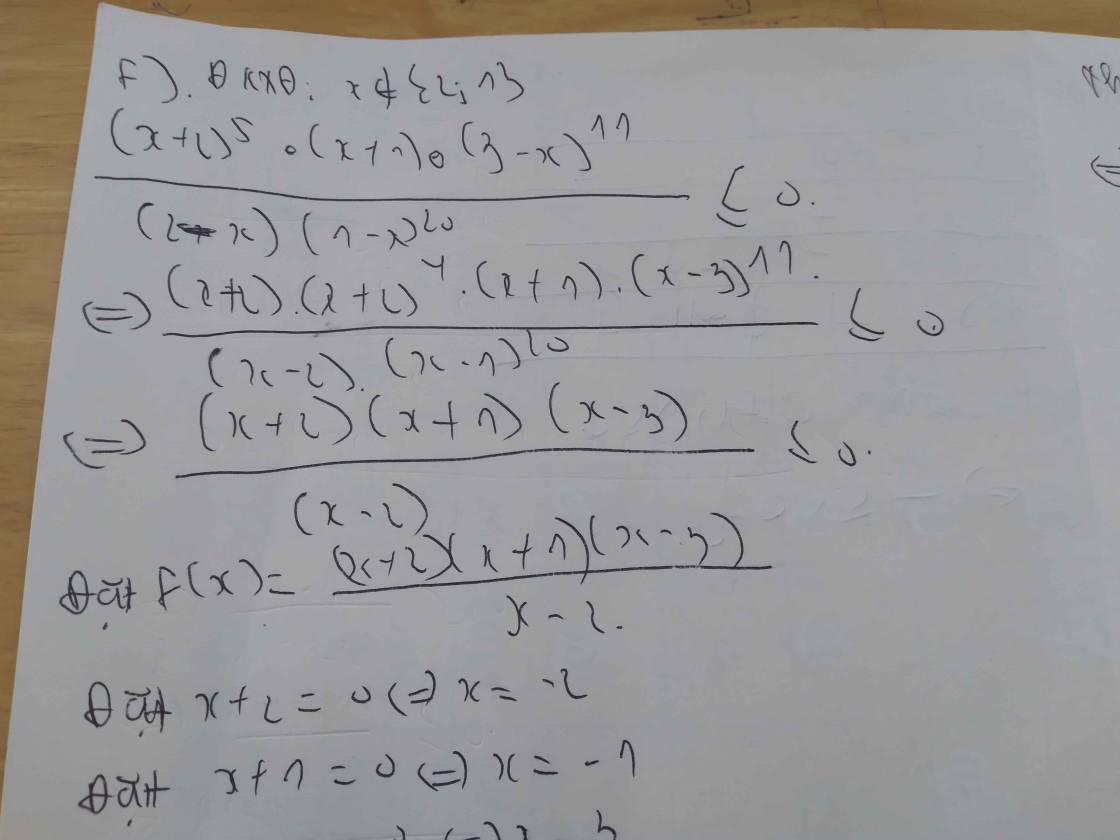Tập nghiệm của bất phương trình \(\dfrac{2x\left(x^2-1\right)}{3-2x-x^2}\le0\) là
H24
Những câu hỏi liên quan
Giải các bất phương trình sau rồi biểu diễn tập nghiệm của chúng trên trục số:1) left(x+3right)^2-3left(2x-1right)xleft(x-4right)2) 1+dfrac{x+1}{3}dfrac{2x-1}{6}-23) x-dfrac{2x-7}{4} dfrac{2x}{3}-dfrac{2x+3}{2}-14) dfrac{2x+1}{x-3}le25) dfrac{12-3x}{2x+6}36) x^2+3x-4le07) dfrac{5}{5x-1} dfrac{-3}{5-3x}8) left(2x-1right)left(3-2xright)left(1-xright)0
Đọc tiếp
Giải các bất phương trình sau rồi biểu diễn tập nghiệm của chúng trên trục số:
1) \(\left(x+3\right)^2-3\left(2x-1\right)>x\left(x-4\right)\)
2) \(1+\dfrac{x+1}{3}>\dfrac{2x-1}{6}-2\)
3) \(x-\dfrac{2x-7}{4}< \dfrac{2x}{3}-\dfrac{2x+3}{2}-1\)
4) \(\dfrac{2x+1}{x-3}\le2\)
5) \(\dfrac{12-3x}{2x+6}>3\)
6) \(x^2+3x-4\le0\)
7) \(\dfrac{5}{5x-1}< \dfrac{-3}{5-3x}\)
8) \(\left(2x-1\right)\left(3-2x\right)\left(1-x\right)>0\)
1: \(\Leftrightarrow x^2+6x+9-6x+3>x^2-4x\)
=>-4x<12
hay x>-3
2: \(\Leftrightarrow6+2x+2>2x-1-12\)
=>8>-13(đúng)
4: \(\dfrac{2x+1}{x-3}\le2\)
\(\Leftrightarrow\dfrac{2x+1-2x+6}{x-3}< =0\)
=>x-3<0
hay x<3
6: =>(x+4)(x-1)<=0
=>-4<=x<=1
Đúng 1
Bình luận (0)
Giải các bất phương trình saua/ (x+1).(x-1).(3x-6)0b/ dfrac{x+3}{x-2}le0c/ dfrac{left(2x-5right).left(x+2right)}{-4x+3}ge0d/ dfrac{2x-5}{3x+2} dfrac{3x+2}{2x-5}e/ dfrac{2x^2+x}{1-2x}ge1-xf/ dfrac{left(2+xright)^5.left(x+1right).left(3-xright)^{11}}{left(2-xright).left(1-xright)^{20}}le0
Đọc tiếp
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
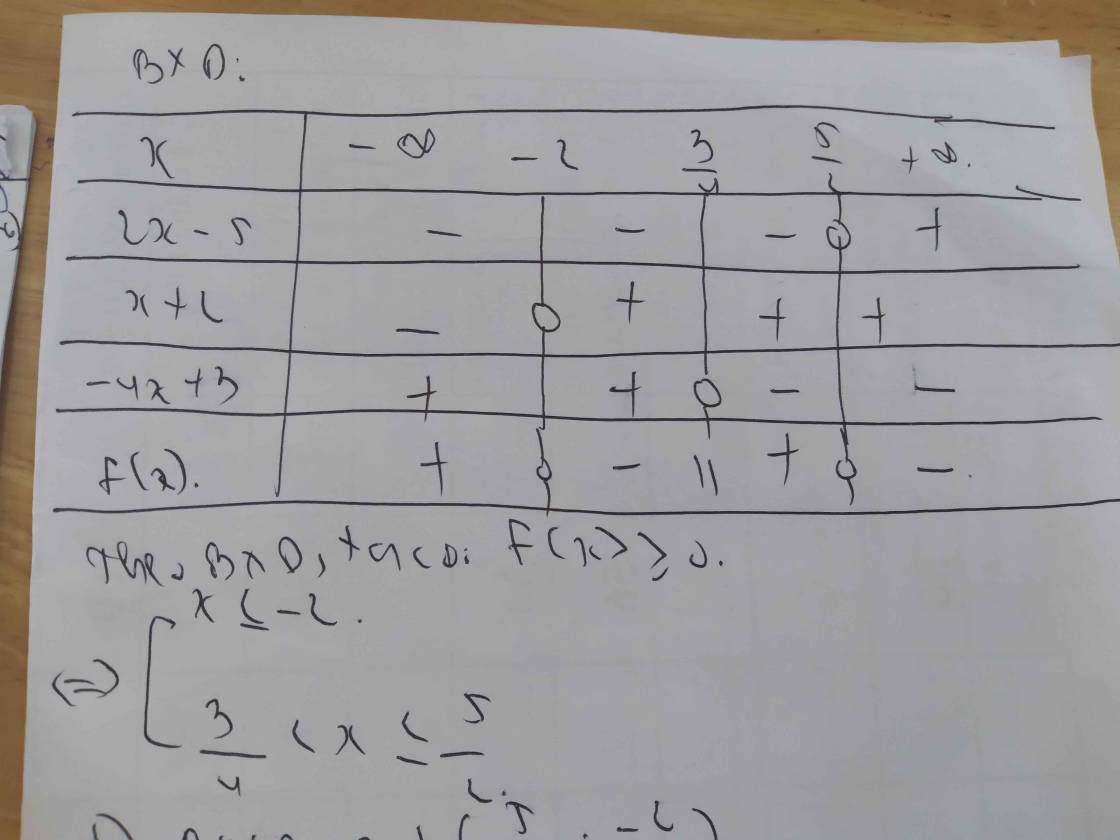
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
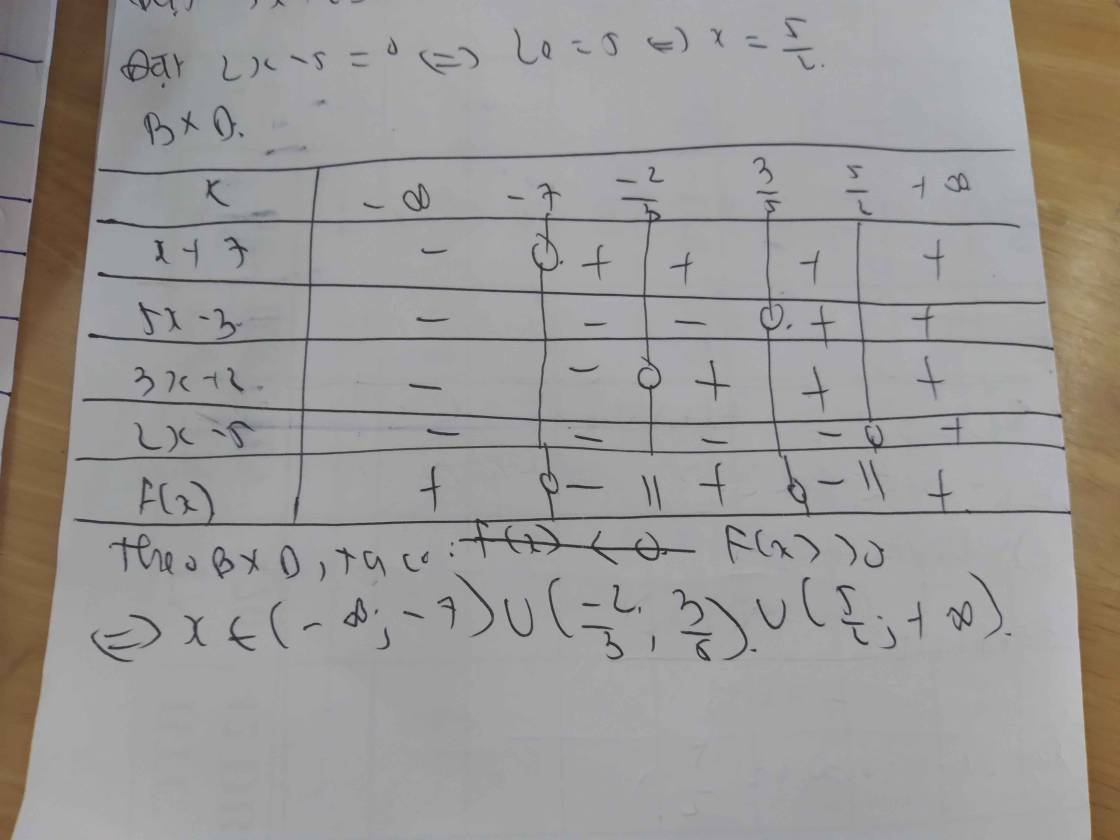
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
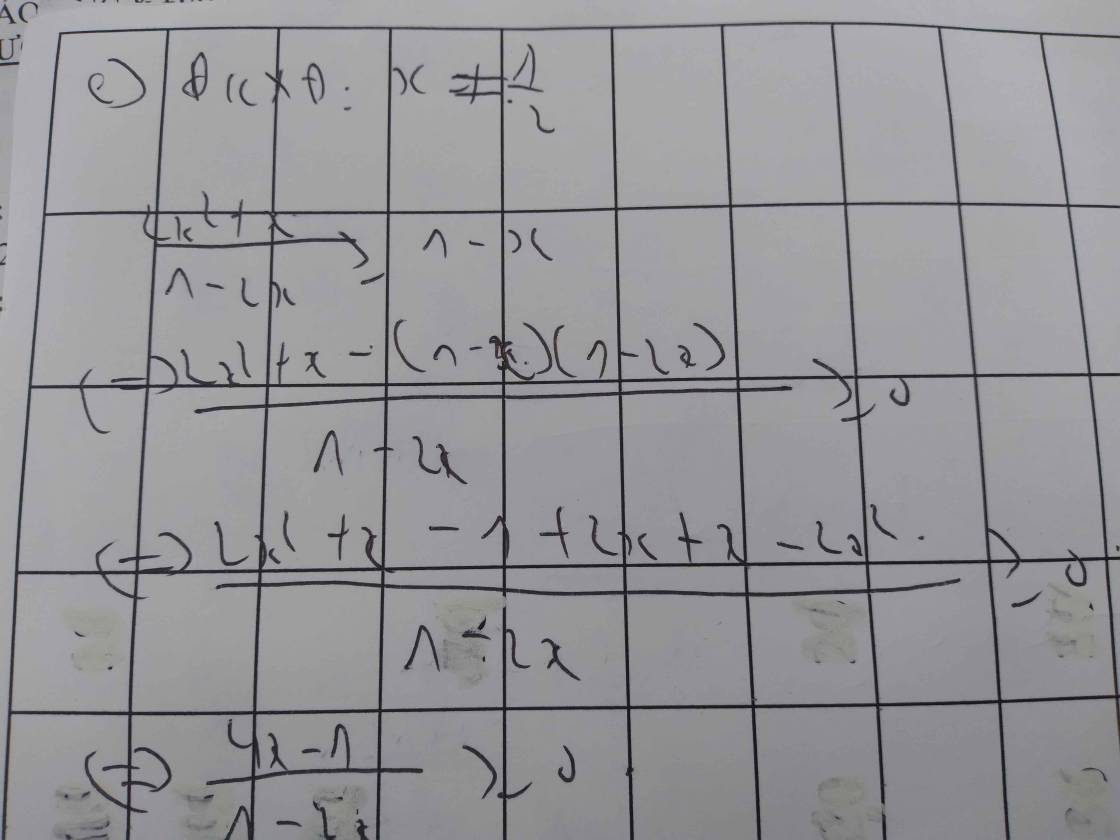
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
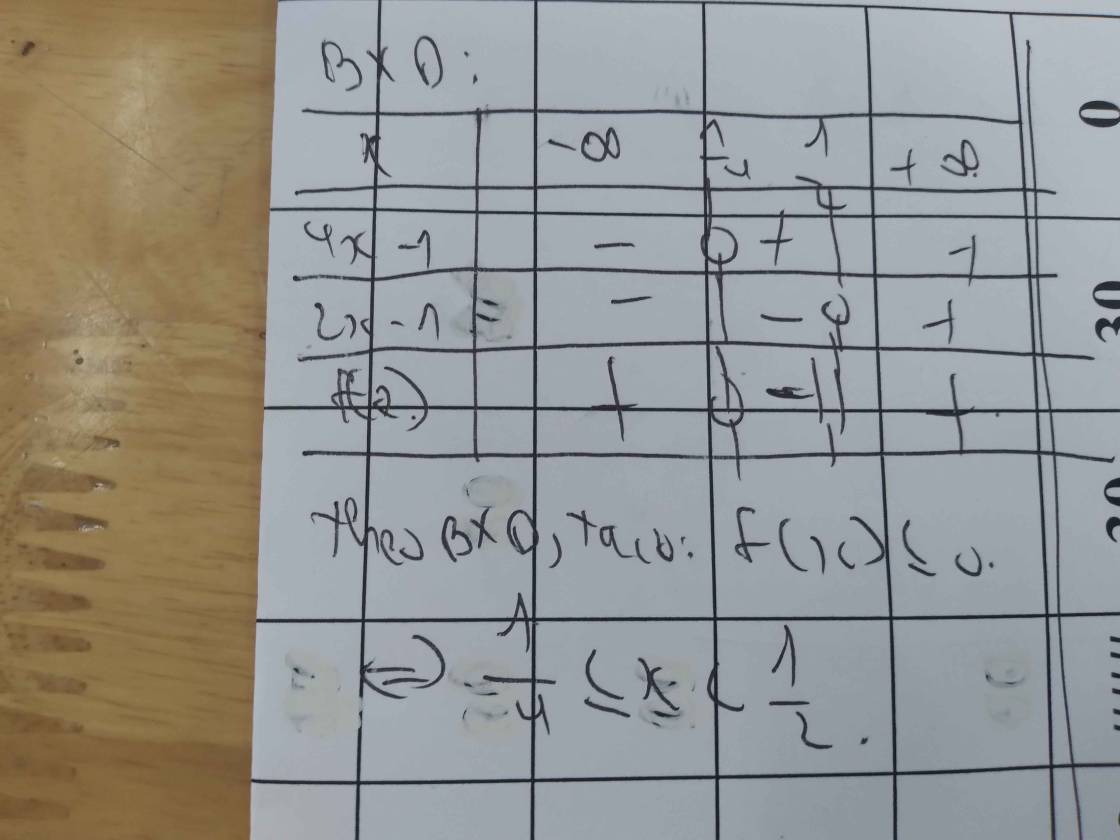
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải các bất phương trình saua/ (x+1).(x-1).(3x-6)0b/ dfrac{x+3}{x-2}le0c/ dfrac{left(2x-5right).left(x+2right)}{-4x+3}ge0d/ dfrac{2x-5}{3x+2} dfrac{3x+2}{2x-5}e/ dfrac{2x^2+x}{1-2x}ge1-xf/ dfrac{left(2+xright)^5.left(x+1right).left(3-xright)^{11}}{left(2-xright).left(1-xright)^{20}}le0
Đọc tiếp
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
Áp dụng giải bất phương trình
\(\dfrac{\left(2x+1\right)^4\left(x-3\right)^3}{\left(x+5\right)^2x^5}\le0\)
Lời giải:
ĐK: $x\neq -5; n\neq 0$
\(\frac{(2x+1)^4(x-3)^3}{(x+5)^2x^5}\leq 0\Leftrightarrow \left[\frac{(2x+1)^2(x-3)}{(x+5)x^2}\right]^2.\frac{x-3}{x}\leq 0\)
\(\Leftrightarrow \frac{x-3}{x}\leq 0\Rightarrow \left[\begin{matrix} x-3\geq 0; x< 0\\ x-3\leq 0; x>0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} 0> x\geq 3(\text{vô lý})\\ 3\geq x>0\end{matrix}\right.\)
Vậy $3\geq x>0$
Đúng 0
Bình luận (0)
Giải bất phương trình sau:
\(\dfrac{\left(6-2x\right)^3\left(x+2\right)^4\left(x+6\right)}{\left(x-7\right)^3\left(2-x\right)^2}\le0\)
7,3, -6
ĐKXĐ: \(x\ne7;x\ne2\)
BPT \(\Leftrightarrow f\left(x\right)=\dfrac{\left(6-2x\right)^3\left(x+6\right)}{\left(x-7\right)^3}\le0\)
Lập bảng xét dấu ta có:
Từ đây ta thấy \(-6\le x\le3\) hoặc \(x>7\) thỏa mãn bất phương trình ban đầu.
Vậy...
Đúng 0
Bình luận (0)
Bài 1: Tìm m để fleft(xright)mx^2-2left(m-1right)x+4m luôn luôn âm.Bài 2: Tìm tất cả các giá trị của tham số m để bất phương trình dfrac{-x^2+2x-5}{x^2-mx+1}le0nghiệm đúng với mọi xin RBài 3: Cho hàm số fleft(xright)-x^2-2left(m-1right)x+2m-1. Tìm tất cả các giá trị của tham số m để fleft(xright)0,forall xinleft(0;1right)
Đọc tiếp
Bài 1: Tìm m để \(f\left(x\right)=mx^2-2\left(m-1\right)x+4m\) luôn luôn âm.
Bài 2: Tìm tất cả các giá trị của tham số m để bất phương trình \(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\)nghiệm đúng với mọi \(x\in R\)
Bài 3: Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số m để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
1.
Nếu \(m=0\), \(f\left(x\right)=2x\)
\(\Rightarrow m=0\) không thỏa mãn
Nếu \(x\ne0\)
Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-1\right)^2-4m^2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m< -\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
2.
\(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\forall x\)
\(\Leftrightarrow\dfrac{-\left(x-1\right)^2-4}{x^2-mx+1}\le0\forall x\)
\(\Leftrightarrow x^2-mx+1>0\forall x\)
\(\Leftrightarrow\Delta=m^2-4< 0\Leftrightarrow-2< m< 2\)
Kết luận: \(-2< m< 2\)
Đúng 0
Bình luận (0)
Tìm m để hệ bất phương trình có nghiệm \(\left\{{}\begin{matrix}-x^2+2x+3\le0\\x+2m-1>0\end{matrix}\right.\)
Xét \(-x^2+2x+3\le0\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge3\end{matrix}\right.\)
Xét \(x+2m-1>0\Leftrightarrow x>-2m+1\)
Hệ đã cho có nghiệm với mọi m (đều chứa khoảng dương vô cùng)
Đúng 1
Bình luận (0)
Tìm m để hệ bất phương trình có nghiệm \(\left\{{}\begin{matrix}-x^2+2x+3\le0\\x+2m-1>0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-x^2+2x+3\le0\\x+2m-1>0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}-1\le x\le3\\x>-2m+1\end{matrix}\right.\)
để pt ....thì \(-2m+1< 3\)
<=>\(-2m< 2\)
<=> \(m>1\)
vậy pt .....
Đúng 0
Bình luận (0)
Tìm m để hệ bất phương trình có nghiệm duy nhấta) left{{}begin{matrix}2x-1ge3x-mle0end{matrix}right.b) left{{}begin{matrix}m^2xge6-x3x-1le x+5end{matrix}right.c) left{{}begin{matrix}left(x-3right)^2ge x^2+7x+12mle8+5xend{matrix}right.d) left{{}begin{matrix}mxle m-3left(m+3right)xge m-9end{matrix}right.e)left{{}begin{matrix}2mleft(x+1right)ge x+34mx+3ge4xend{matrix}right.
Đọc tiếp
Tìm m để hệ bất phương trình có nghiệm duy nhất
a) \(\left\{{}\begin{matrix}2x-1\ge3\\x-m\le0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}m^2x\ge6-x\\3x-1\le x+5\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge x^2+7x+1\\2m\le8+5x\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}mx\le m-3\\\left(m+3\right)x\ge m-9\end{matrix}\right.\)
e)\(\left\{{}\begin{matrix}2m\left(x+1\right)\ge x+3\\4mx+3\ge4x\end{matrix}\right.\)
a.
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x\le m\end{matrix}\right.\)
Hệ có nghiệm duy nhất \(\Leftrightarrow m=2\)
b.
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m^2+1\right)x\ge6\\2x\le6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{6}{m^2+1}\\x\le3\end{matrix}\right.\)
Hệ có nghiệm duy nhất \(\Leftrightarrow\dfrac{6}{m^2+1}=3\)
\(\Leftrightarrow m=\pm1\)
c.
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+9\ge x^2+7x+1\\5x\ge2m-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{8}{13}\\x\ge\dfrac{2m-8}{5}\end{matrix}\right.\)
Pt có nghiệm duy nhất khi \(\dfrac{2m-8}{5}=\dfrac{8}{13}\Leftrightarrow m=\dfrac{72}{13}\)
Đúng 2
Bình luận (0)
d.
Hệ có nghiệm duy nhất khi:
TH1:
\(\left\{{}\begin{matrix}m>0\\\dfrac{m-3}{m}=\dfrac{m-9}{m+3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m^2-9=m^2-9m\end{matrix}\right.\) \(\Leftrightarrow m=1\)
TH2:
\(\left\{{}\begin{matrix}m+3< 0\\\dfrac{m-3}{m}=\dfrac{m-9}{m+3}\end{matrix}\right.\)
\(\Leftrightarrow m=1\) (ktm)
Vậy \(m=1\)
e.
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2m-1\right)x\ge-2m+3\\\left(4-4m\right)x\le3\end{matrix}\right.\)
Hệ có nghiệm duy nhất khi:
\(\left\{{}\begin{matrix}\left(2m-1\right)\left(4-4m\right)>0\\\dfrac{-2m+3}{2m-1}=\dfrac{3}{4-4m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}< m< 1\\\left[{}\begin{matrix}m=\dfrac{3}{4}\\m=\dfrac{5}{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow m=\dfrac{3}{4}\)
Đúng 1
Bình luận (0)