giải hệ pt sau
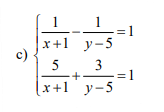
Giải hệ pt sau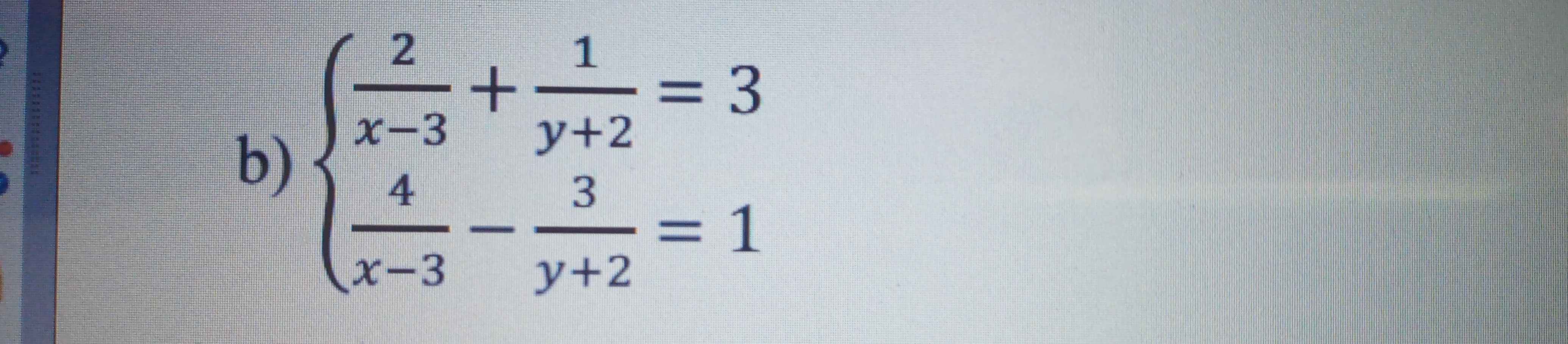
Đặt \(\dfrac{1}{x-3}=a;\dfrac{1}{y+2}=b\)
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2a+b=3\\4a-3b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=1\\y+2=1\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(4;-1\right)\)
giải hệ pt sau
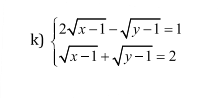
ĐKXĐ: \(x\ge1;y\ge1\)
\(\left\{{}\begin{matrix}2\sqrt{x-1}-\sqrt{y-1}=1\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-1}=3\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{y-1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=1\\y-1=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
giải hệ pt sau:
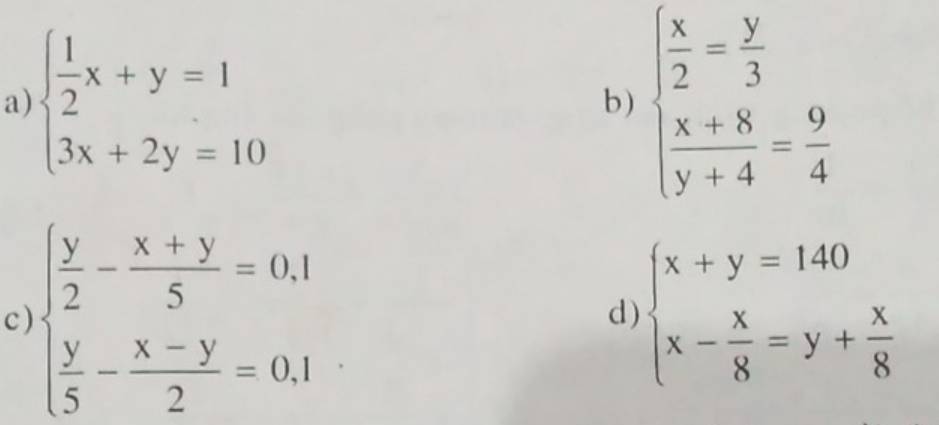
giải hệ pt sau
a: \(\left\{{}\begin{matrix}\dfrac{1}{2}x+y=1\\3x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=2\\3x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-8\\x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\2y=2-x=2-4=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=-1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{x+8}{y+4}=\dfrac{9}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=2y\\4\left(x+8\right)=9\left(y+4\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=0\\4x-9y=36-32=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-8y=0\\12x-27y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-12\\3x-2y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{12}{19}\\3x=2y=2\cdot\dfrac{-12}{19}=-\dfrac{24}{19}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{8}{19}\\y=-\dfrac{12}{19}\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{y}{2}-\dfrac{x+y}{5}=0,1\\\dfrac{y}{5}-\dfrac{x-y}{2}=0,1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5y-2\left(x+y\right)}{10}=\dfrac{1}{10}\\\dfrac{2y-5\left(x-y\right)}{10}=\dfrac{1}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5y-2x-2y=1\\2y-5x+5y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+3y=1\\-5x+7y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-10x+15y=5\\-10x+14y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\2x-3y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\2x=3y-1=3\cdot3-1=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}x+y=140\\x-\dfrac{x}{8}=y+\dfrac{x}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=140\\\dfrac{3}{4}x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{4}x=140\\x+y=140\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=140:\dfrac{7}{4}=140\cdot\dfrac{4}{7}=80\\y=140-80=60\end{matrix}\right.\)
Tìm điều kiện xác định của pt và giải hệ pt sau :
x2- căn (1-x) = căn ( x-2 ) + 3
\(x-\sqrt{1-x}=\sqrt{x-2}+3\)
\(ĐK:\left\{{}\begin{matrix}1-x\ge0\\x-2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\x\ge2\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
Vậy PT vô nghiệm
giải hệ pt sau:
{√x + 2√y-1 =5
4√x - √y-1 =2
Ta có:
\(\left\{{}\begin{matrix}\sqrt{x}+2\sqrt{y-1}=5\\4\sqrt{x}-\sqrt{y-1}=2\end{matrix}\right.\) (đk \(x\ge0,y\ge1\))
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2\sqrt{y-1}=5\\8\sqrt{x}-2\sqrt{y-1}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9\sqrt{x}=9\\\sqrt{x}+2\sqrt{y-1}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=1\\1+2\sqrt{y-1}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\2\sqrt{y-1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y-1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\left(tm\right)\)
bạn ê làm bài gì trong lhó thế
giải ra x=1,y-1 Nhưng viết trên đây khó quá @_@
Giải hệ PT sau:
\(\begin{cases} \dfrac{1}{2}x - y = 1\\ x - 2y = 2 \end{cases}\)
\(\left\{{}\begin{matrix}\dfrac{1}{2}x-y=1\\x-2y=2\end{matrix}\right.=>\left\{{}\begin{matrix}\dfrac{1}{2}x-y=1\\\dfrac{1}{2}x-y=1\end{matrix}\right.\)
=> phương trình có vô số nghiệm
giải hệ pt và pt sau:
a) 3x-2y=3 và 2x+2y=2
b) x^2+7x-12=0
a)\(\left\{{}\begin{matrix}3x-2y=3\\2x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=5\\3x-2y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\3-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
b)\(x^2+7x+12=0\)
\(\Leftrightarrow x^2+3x+4x+12=0\)( chị nghĩ + 12 đúng hơn á )
\(\Leftrightarrow x\left(x+3\right)+4\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+3=0\\x+4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-3\\x=-4\end{matrix}\right.\)