Giúp em câu 26 đến 28 với ạ 
H24
Những câu hỏi liên quan
Giúp em câu 28 với ạ

Giúp em làm với ạ từ 2 đến 28

5 C
3 D
4 C
5 C
6 C
7 A
8 C
9 C
10 D
11 C
12 C
13 D
14 D
15 A
16 C
17 B
18A
19 D
20 D
21 C
22 B
23 B
24 D
25 A
26 B
27 B
28 B
Đúng 2
Bình luận (0)
Giúp em câu 27 28 29 với ạ:(
28:
a: \(AB=\sqrt{\left(6-0\right)^2+\left(4-2\right)^2}=2\sqrt{10}\)
\(AC=\sqrt{1^2+\left(-1-2\right)^2}=\sqrt{10}\)
\(BC=\sqrt{\left(1-6\right)^2+\left(-1-4\right)^2}=5\sqrt{2}\)
Vì AB^2+AC^2=BC^2
nên ΔABC vuông tại A
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=10\)
b: B(6;4); C(1;-1); D(3;1)
\(\overrightarrow{BD}=\left(-3;-3\right);\overrightarrow{BC}=\left(-5;-5\right)\)
Vì -3/-5=-3/-5
nên B,D,C thẳng hàng
c: ABCD là hình bình hành
=>vecto AB=vecto DC
vecto AB=(6;2); vecto DC=(1-x;-1-y)
vecto AB=vecto DC
=>1-x=6 và -1-y=2
=>x=-5 và y=-3
Đúng 0
Bình luận (0)
giúp em giải câu 28 29 30 với ạ

mọi người giúp em từ câu 22 -> 28 với ạ

16) 2/3+2/7-1/14
phần → ___________
-1-3/7+3/28
có 1 câu thôi ạ tử và mẫu là phân số và đều là phép tính giúp em với ạ giải thích giúp em với
Giúp em câu 10 đến 17 với ạ. Em đang cần gấp ạ
10.
\(\dfrac{sin3x-cos3x}{sinx+cosx}=\dfrac{3sinx-4sin^3x-\left(4cos^3x-3cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(1-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{\left(sinx+cosx\right)\left(3-4+4sinx.cosx\right)}{sinx+cosx}\)
\(=-1+4sinx.cosx\)
\(=2sin2x-1\)
Đúng 1
Bình luận (0)
11.
\(tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{1+cos\left(\dfrac{\pi}{2}+x\right)}{sin\left(\dfrac{\pi}{2}+x\right)}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1+sin\left(-x\right)}{cos\left(-x\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1-sinx}{cosx}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}-2sin\dfrac{x}{2}cos\dfrac{x}{2}}{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)^2}{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)\left(cos\dfrac{x}{2}+sin\dfrac{x}{2}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\dfrac{x}{2}-sin\dfrac{x}{2}}{cos\dfrac{x}{2}+sin\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}{sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).cot\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\)
\(=1\)
Đúng 1
Bình luận (0)
12.
\(cot2x+\dfrac{1}{sin2x}+tanx=\dfrac{cos2x}{sin2x}+\dfrac{1}{sin2x}+tanx\)
\(=\dfrac{cos2x+1}{sin2x}+\dfrac{sinx}{cosx}=\dfrac{2cos^2x-1+1}{2sinx.cosx}+\dfrac{sinx}{cosx}\)
\(=\dfrac{2cos^2x}{2sinx.cosx}+\dfrac{sinx}{cosx}=\dfrac{cosx}{sinx}+\dfrac{sinx}{cosx}\)
\(=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}\)
\(=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Mọi người cho em hỏi từ câu 20 đến câu 28 em làm đúng chưa ạ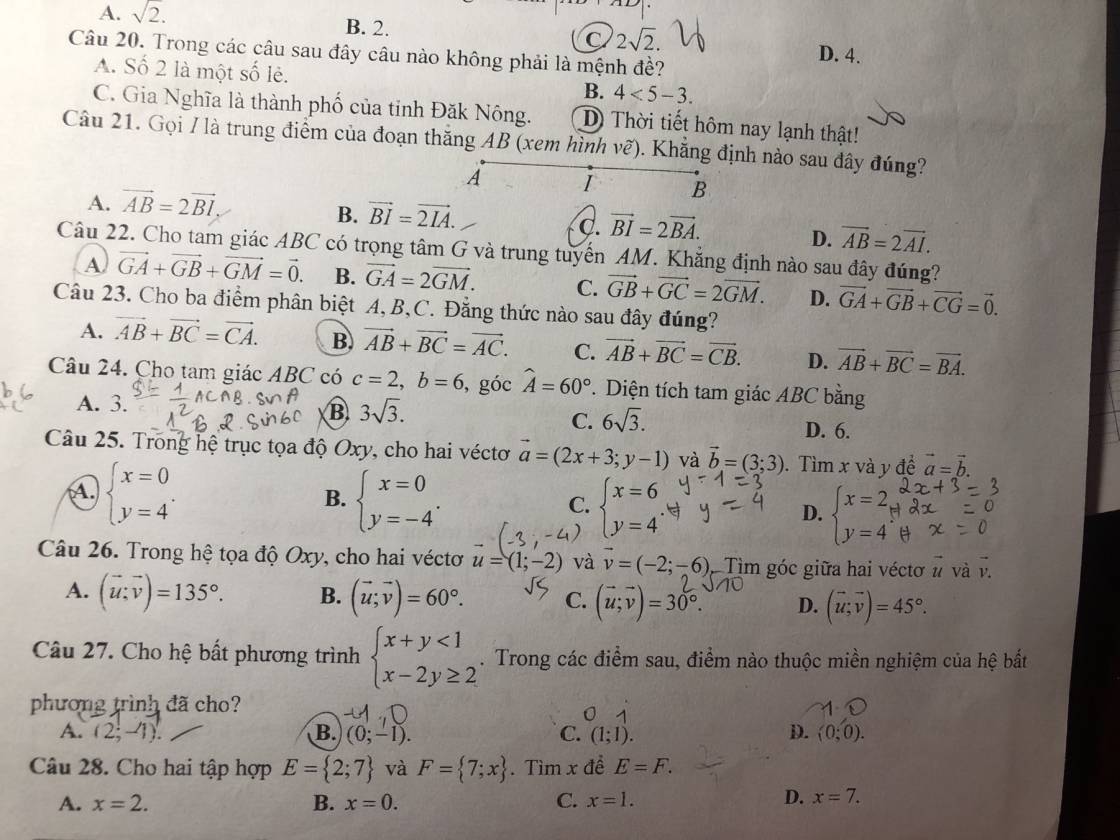
Câu 21: D
Câu 22: D
Câu 26: D
Câu 28: A
Đúng 1
Bình luận (0)
Anh chị nào giúp mình câu 26 và 28 với




