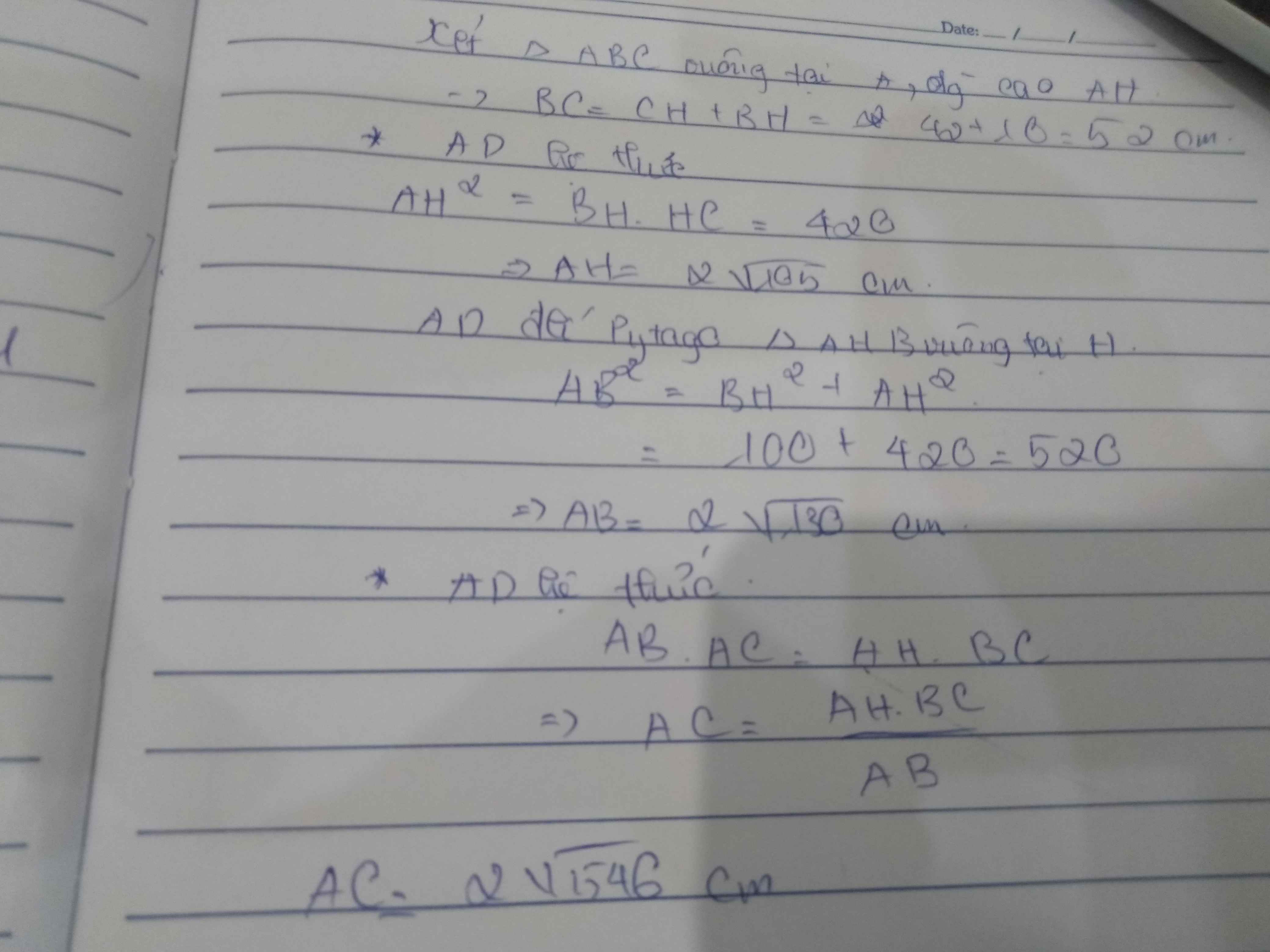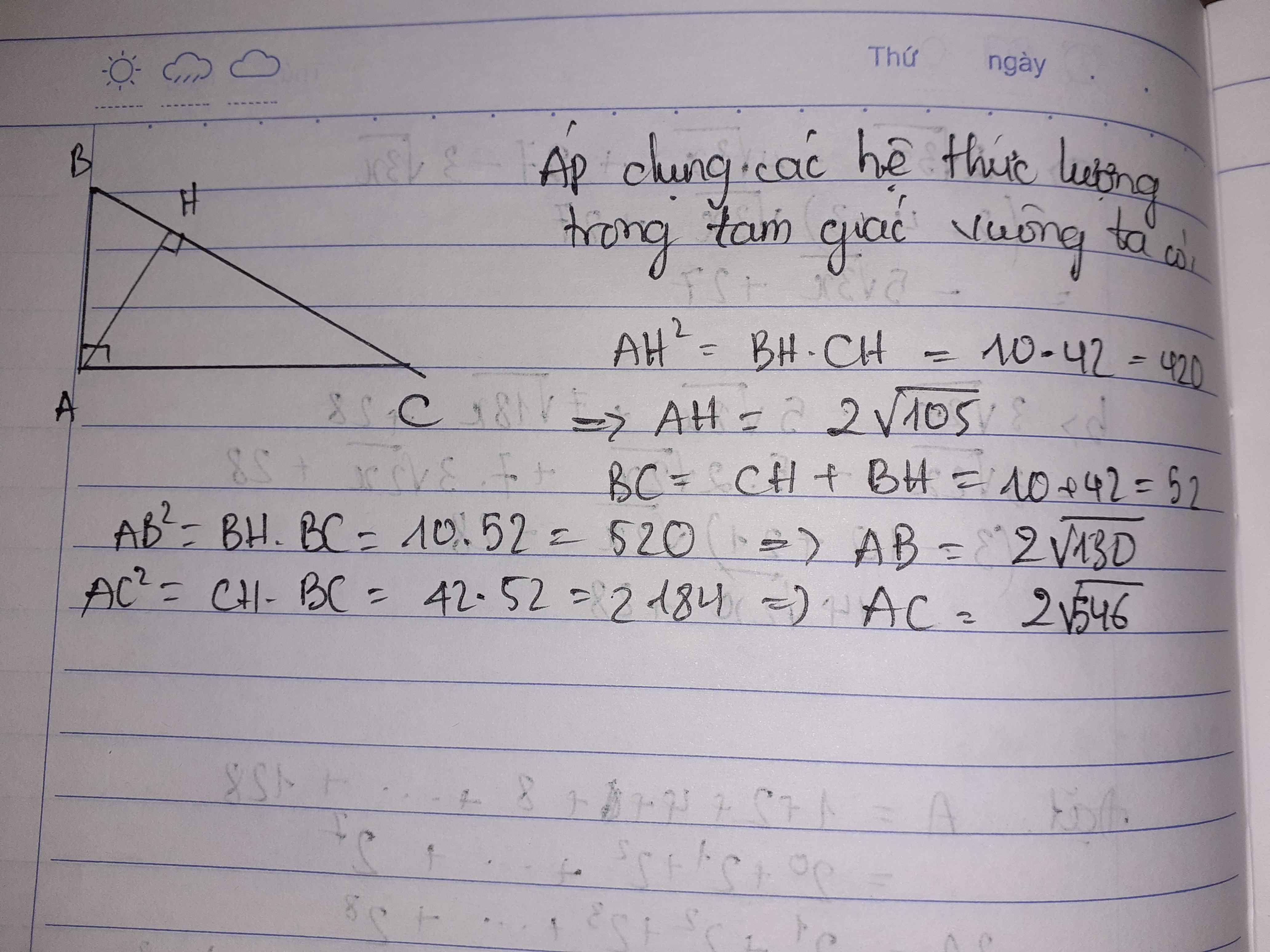Cho tam giác ABC vuông tại A có đường cao AH. Có AB/AC = 3/7, AH = 42cm. Tính BH, CH
NN
Những câu hỏi liên quan
* Cho tam giác ABC vuông tại A có đường cao AH. Biết BH=10cm, CH =42cm. Tính BC, AH, AB và AC
Cho tam giác ABC vuông tại A, đường cao AH. Biết \(\dfrac{AB}{AC}\)=\(\dfrac{3}{7}\) và đường cao AH=42cm. Tính BH, HC
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
nên \(AB=\dfrac{3}{7}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{7}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{1}{42^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{49}AC^2}+\dfrac{\dfrac{9}{49}}{\dfrac{9}{49}AC^2}=\dfrac{1}{1764}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{49}=2088\)
\(\Leftrightarrow AC^2=11368\)
\(\Leftrightarrow AC=14\sqrt{58}\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{7}\cdot14\sqrt{58}=6\sqrt{58}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=\left(6\sqrt{58}\right)^2+\left(14\sqrt{58}\right)^2=13456\)
hay BC=116(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(6\sqrt{58}\right)^2}{116}=18\left(cm\right)\\CH=\dfrac{AC^2}{CH}=\dfrac{\left(14\sqrt{58}\right)^2}{116}=98\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Biết BH = 10cm , CH = 42cm . Tính BC , AH , AB , AC.
\(BC=BH+CH=52\left(cm\right)\)
\(AH=\sqrt{BH.CH}=2\sqrt{105}\) (cm)
\(AB^2=BH.BC\Rightarrow AB=\sqrt{BH.BC}=2\sqrt{130}\left(cm\right)\)
\(AC^2=CH.BC\Rightarrow AC=\sqrt{CH.BC}=2\sqrt{546}\left(cm\right)\)
Đúng 5
Bình luận (0)
Ta có: BC=BH+CH(H nằm giữa B và C)
nên BC=10+42=52(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=10\cdot42=420\)
hay \(AH=2\sqrt{105}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{105}\right)^2+10^2=420+100=520\)
hay \(AB=2\sqrt{130}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=52^2-520=2184\)
hay \(AC=2\sqrt{546}\left(cm\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A đường cao AH, biết BH=10cm, CH=42cm. Tính cạnh BC, AH, AB và AC
Ta có: BC=BH+CH
nên BC=10+42=52cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{105}cm\\AB=2\sqrt{130}cm\\AC=2\sqrt{546}cm\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH
a)Cho Hb/Hc=9/16 và AH=48cm tính AB và AC
b)Cho AB/AC=3/4 và BC=125cm.Tính AH
c)Cho AB/ACC= 3/7 và AH= 42cm. Tính BH và CH
cảm ơn ạ
câu a là HB/HC ạ , em quên viết hoa
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết BH=10cm, CH=42cm. Tính cạnh BC, AH, AB và AC ( vẽ hình giúp )
Cho tam giác ABC vuông tại A có đường cao AH . Biết BH=10cm; CH=42cm. Tính độ dài của vectơ AB
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài các đoạn thẳng CH
A. CH = 96
B. CH = 49
C. CH = 98
D. CH = 89

Ta có: AB : AC = 3 : 7, đặt AB = 3a; AC = 7a (a > 0)
Theo hệ thức lượng: 1 A H 2 = 1 A B 2 + 1 A C 2 ⇒ 1 42 = 1 9 a 2 + 1 49 a 2 ⇒ 1 1764 = 58 441 a 2
⇒ 441 2 = 102312 ⇒ A = 2 58 ( T M ) ⇒ A B = 6 58 ; A C = 14 58
Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
CH = A C 2 − A H 2 = 14 58 2 − 42 2 = 98
Vậy CH = 98
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có đường cao ah,trung tuyến am
a.biết bc=125cm,ab/ac=3/4.tính bh,ch
b.biết ah=42cm,ab/ac=3/7.tính độ dài hình chiếu của mỗi cạnh góc vuông trên cạnh huyền
c.biết ah=48cm,hb/hc=9/16.tính ab,ac,bc
d.biết ab/am=8/5.tính tỉ số ab/ac
a: AB/AC=3/4
=>BH/CH=9/16
=>BH/9=CH/16=(BH+CH)/(9+16)=125/25=5
=>BH=45cm; CH=80cm
b: AB/AC=3/7
=>HB/HC=(3/7)^2=9/49
=>HB/9=HC/49=k
=>HB=9k; HC=49k
AH^2=HB*HC
=>9k*49k=42^2
=>k=2
=>HB=18cm; HC=98cm
c: Đặt HB/9=HC/16=k
=>HB=9k; HC=16k
AH^2=HB*HC
=>144k^2=48^2
=>k=4
=>HB=36cm; HC=64cm
BC=36+64=100cm
AB=căn 36*100=60cm
AC=căn 64*100=80cm
Đúng 0
Bình luận (0)