Cho hình vuông ABCD , E là điểm trên cạnh DC ;F là điểm trên tia đối của tia bc sao cho BF=DE.
a/ Chứng minh tam giác AEF vuông cân .
b/Gọi i là trung điểm EF . Chứng minh i thuộc BD
c/ Lấy K đối xứng với A qua i . Chứng minh tứ giác AEKF là hinh vuông .
DM
Những câu hỏi liên quan
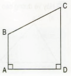
Cho hình chữ nhật ABCD và điểm E trên cạnh AB
Hãy vẽ đường thẳng đi qua điểm E và vuông góc với cạnh DC, cắt cạnh DC tại điểm G. Ta thu được các hình tứ giác đều là hình chữ nhật, nêu tên các hình chữ nhất đó.
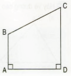
- Các hình chữ nhật là : ABCD, AEGD, EBCG
Đúng 0
Bình luận (0)
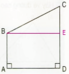
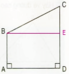
Cho hình chữ nhật ABCD và điểm E trên cạnh AB
Hãy vẽ đường thẳng đi qua điểm E và vuông góc với cạnh DC, cắt cạnh DC tại điểm G. Ta thu được các hình tứ giác đều là hình chữ nhật, nêu tên các hình chữ nhất đó.
Các hình chữ nhật là : ABCD, AEGD, EBCG
Đúng 0
Bình luận (0)
cho hình vuông abcd trên dc ta lấy điểm e sao cho dt bằng 1/3 dc biết diện tích hình tam giác abe là 5,36 cm2 tính diện tích hình vuông abcdcho hình vuông abcd trên dc ta lấy điểm e sao cho dt bằng 1/3 dc biết diện tích hình tam giác abe là 5,36 cm2 tính diện tích hình vuông abcdcho hình vuông abcd
TM
7 tháng 11 2021 lúc 21:35
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC
THầy cô giúp e với
Cho hình vuông ABCD . Trên cạnh BC lấy điểm E , trên tia đối của tia DC lấy điểm F sao cho BE = DF .
a) Chứng minh ΔAEH vuông cân tại A
b) Gọi H là điểm đối xứng của A qua EF . Chứng minh AEHF là hình vuông.
a: Sửa đề: ΔAEF vuông cân tại A
Xét ΔADF vuông tại D và ΔABE vuông tại B có
AD=AB
DF=BE
Do đó: ΔADF=ΔABE
=>AF=AE và \(\widehat{DAF}=\widehat{BAE}\)
mà \(\widehat{BAE}+\widehat{DAE}=90^0\)
nên \(\widehat{DAF}+\widehat{DAE}=90^0\)
=>\(\widehat{FAE}=90^0\)
Xét ΔAEF có \(\widehat{FAE}=90^0\) và AE=AF
nên ΔAEF vuông cân tại A
b: Gọi giao điểm của AH với EF là M
H đối xứng A qua EF
=>EF là đường trung trực của HA
=>EH=EA và FH=FA
mà AH=AE
nên EH=EA=FH=FA
Xét tứ giác AEHF có
AE=HE=HF=FA
nên AEHF là hình thoi
Hình thoi AEHF có \(\widehat{FAE}=90^0\)
nên AEHF là hình vuông
Đúng 2
Bình luận (0)
TM
7 tháng 11 2021 lúc 21:18
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC
TM
7 tháng 11 2021 lúc 22:29
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC
TM
7 tháng 11 2021 lúc 22:33
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC
TM
8 tháng 11 2021 lúc 19:29
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC
TM
8 tháng 11 2021 lúc 20:09
cho hình vuông ABCD . Trên AD lấy điểm F .Trên cạnh DC lấy điểm E . Trên AB lấy điểm G sao cho AF=DE=AG . Gọi I là giao điểm của AE và BF . cmr IG vuông góc với IC
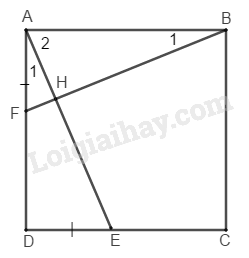
Xét ΔABF và ΔDAE ta có:
AB=DA (gt)
ˆBAF=ˆADE=900
AF=DE (gt)
Do đó: ΔABF=ΔDAE(c.g.c)
⇒BF=AE và ˆB1=ˆA1
Gọi H là giao điểm của AE và BF
ˆBAF=ˆA1+ˆA2=900
⇒ ˆB1+ˆA2=900
Trong ΔABH ta có:
ˆAHB+ˆB1+ˆA2=1800
ˆAHB=1800−(ˆB1+ˆA2)=1800−900=900
Vậy AE⊥BF
Đúng 0
Bình luận (1)
Xét ΔABF và ΔDAE ta có:
AB=DA (gt)
ˆBAF=ˆADE=900
AF=DE (gt)
Do đó: ΔABF=ΔDAE(c.g.c)
⇒BF=AE và ˆB1=ˆA1
Gọi H là giao điểm của AE và BF
ˆBAF=ˆA1+ˆA2=900
⇒ ˆB1+ˆA2=900
Trong ΔABH ta có:
ˆAHB+ˆB1+ˆA2=1800
ˆAHB=1800−(ˆB1+ˆA2)=1800−900=900
Vậy AE⊥BF
Đúng 0
Bình luận (0)