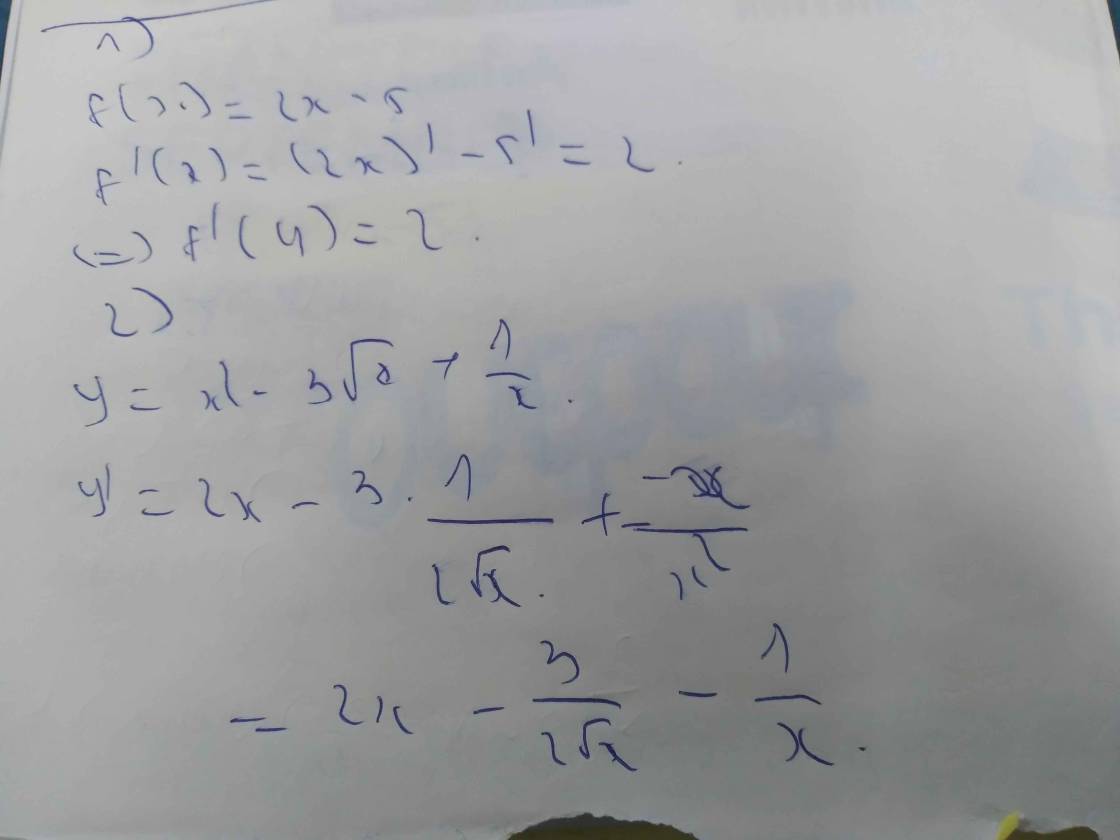cho hàm số \(y=\dfrac{1}{x^2-2x+5}\). có bao nhiêu số nguyen \(x\in\left(-9;9\right)\) để \(y'\left(x\right)\ge0\)
JE
Những câu hỏi liên quan
1. Đạo hàm của hàm số y= \(\left(x^3-5\right).\sqrt{x}\) bằng bao nhiêu?
2. Đạo hàm của hàm số y= \(\dfrac{1}{2}x^6-\dfrac{3}{x}+2\sqrt{x}\) là?
3. Hàm số y= \(2x+1+\dfrac{2}{x-2}\) có đạo hàm bằng?
1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)
2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)
3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)
Đúng 1
Bình luận (0)
Cho hàm đa thức yleft[fleft(x^2+2xright)right] có đồ thị cắt trục Ox tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số m2022min Z để hàm số gleft(xright)fleft(x^2-2left|x-1right|-2x+mright) có 9 điểm cực trị?Giúp mình với ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho hàm đa thức \(y=\left[f\left(x^2+2x\right)\right]'\) có đồ thị cắt trục \(Ox\) tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số \(m=2022m\in Z\) để hàm số \(g\left(x\right)=f\left(x^2-2\left|x-1\right|-2x+m\right)\) có 9 điểm cực trị?
Giúp mình với ạ, mình cảm ơn nhiều♥
đề bài thiếu, ko giải được, cái nghiệm -1 có thể của f(u) hoặc của u'
Đúng 0
Bình luận (1)
cho hàm số \(y=\dfrac{x^2+2x-3}{x+2}\). có bao nhiêu giá trị m để \(y'\left(-1\right)=4\)
Hình như là đề sai, hàm số ko có tham số m nào
Đúng 0
Bình luận (0)
Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\), có bao nhiêu giá trị nguyên của tham số a \(\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
1.lim_{x-infty} sqrt{16x^2-3x+5} +2x-5 2. Tổng tất cả các số hạng của cấp số nhân: -dfrac{1}{3};dfrac{1}{9};-dfrac{1}{27};...;dfrac{left(-1right)^n}{3^n};... bằng bao nhiêu?3. Tìm m để đồ thị hàm số y(2m-1)x4-2x2+3m+5 tại điểm có hoành độ x1 vuông góc với đường thẳng d:5x-y-20180?4. Gọi hình chóp tứ giác đều có tất cả các cạnh bằng 5a. Gọi varphilà góc giữa 1 mặt bên bất kì với mặt đáy. Khẳng đinh nào sau đây đúng?A. sin varphidfrac{sqrt{6}}{3}B. sin varphidfrac{sqrt{3}}{3}C. sin varphidfrac{sqr...
Đọc tiếp
1.lim\(_{x->\infty}\) \(\sqrt{16x^2-3x+5}\) +2x-5
2. Tổng tất cả các số hạng của cấp số nhân: -\(\dfrac{1}{3}\);\(\dfrac{1}{9}\);-\(\dfrac{1}{27}\);...;\(\dfrac{\left(-1\right)^n}{3^n}\);... bằng bao nhiêu?
3. Tìm m để đồ thị hàm số y=(2m-1)x4-2x2+3m+5 tại điểm có hoành độ x=1 vuông góc với đường thẳng d:5x-y-2018=0?
4. Gọi hình chóp tứ giác đều có tất cả các cạnh bằng 5a. Gọi \(\varphi\)là góc giữa 1 mặt bên bất kì với mặt đáy. Khẳng đinh nào sau đây đúng?
A. sin \(\varphi\)=\(\dfrac{\sqrt{6}}{3}\)
B. sin \(\varphi\)=\(\dfrac{\sqrt{3}}{3}\)
C. sin \(\varphi\)=\(\dfrac{\sqrt{2}}{2}\)
D. sin \(\varphi\)=\(\dfrac{2\sqrt{2}}{3}\)
5. Cho tứ diện S.ABC có (SBC) và (ABC) là 2 tam giác đều cạnh a, SA=\(\dfrac{a\sqrt{3}}{2}\). M là 1 điểm trên AB sao cho AM=\(\dfrac{2a}{3}\), gọi (P) là mp qua M và vuông góc với BC. Thiết diện của (P) và tứ diện A.ABC có diện tích bằng bao nhiêu?
1/ \(=\lim\limits_{x\rightarrow-\infty}x\left(-\sqrt{\dfrac{16x^2}{x^2}-\dfrac{3x}{x^2}+\dfrac{5}{x^2}}+2-\dfrac{5}{x}\right)=\lim\limits_{x\rightarrow-\infty}x\left(-4+2\right)=-\infty\)
\(=\lim\limits_{x\rightarrow+\infty}x\left(\sqrt{\dfrac{16x^2}{x^2}-\dfrac{3x}{x^2}+\dfrac{5}{x^2}}+2-\dfrac{5}{x}\right)=\lim\limits_{x\rightarrow+\infty}x\left(4+2\right)=+\infty\)
2/ \(S=\dfrac{-\dfrac{1}{3}}{1+\dfrac{1}{3}}=-\dfrac{1}{4}\)
4/ 
5/ 
Đúng 2
Bình luận (0)
\(f'\left(x\right)=4\left(2m-1\right)x^3-4x\)
Vì tiếp tuyến vuông góc với \(y=5x-2018\Rightarrow f'\left(x\right)=-\dfrac{1}{5}\)
\(\Rightarrow f'\left(1\right)=-\dfrac{1}{5}\Leftrightarrow4\left(2m-1\right)-4=-\dfrac{1}{5}\Leftrightarrow m=\dfrac{39}{40}\)
Đúng 1
Bình luận (0)
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
Đúng 3
Bình luận (0)
a) Cho hàm số yx^2+2x+3+left|x-a+1right| có bao nhiêu giá trị nguyên của tham số ainleft[-10;10right] sao cho giá trị nhỏ nhất của hàm số lớn hơn 2b) Tìm tất cả các giá trị của tham số m để hệ bất pt left{{}begin{matrix}x^2-2x-3le0x^2-2mx+m^2-9ge0end{matrix}right. có nghiệmc) Gọi (x;y) là nghiệm của hệ bất pt left{{}begin{matrix}x-2y-2le04x-3y+12ge0x+3y+3ge02x+y-4le0end{matrix}right.. Tìm giá trị lớn nhất của biểu thức F4x+5y-6
Đọc tiếp
a) Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\) có bao nhiêu giá trị nguyên của tham số \(a\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
b) Tìm tất cả các giá trị của tham số m để hệ bất pt \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\) có nghiệm
c) Gọi (x;y) là nghiệm của hệ bất pt \(\left\{{}\begin{matrix}x-2y-2\le0\\4x-3y+12\ge0\\x+3y+3\ge0\\2x+y-4\le0\end{matrix}\right.\). Tìm giá trị lớn nhất của biểu thức F=4x+5y-6
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m \(\in\left(-20;20\right)\) để hàm số y = \(\dfrac{x-1}{x-m}\) nghịch biến trên khoảng \(\left(-\infty;2\right)\)
\(y'=\dfrac{x-m-x+1}{\left(x-m\right)^2}=\dfrac{1-m}{\left(x-m\right)^2}\)
Hàm số nghịch biến trên khoảng \(\left(-\infty;2\right)\Leftrightarrow y'< 0\forall x\in\left(-\infty;2\right)\Leftrightarrow\left\{{}\begin{matrix}1-m< 0\\x\ne m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge2\end{matrix}\right.\Rightarrow m\ge2\)
Có 19-2+1=18 giá trị nguyên của m thỏa mãn
Đúng 1
Bình luận (0)
Cho hàm số \(y=\dfrac{2sinx+1}{\sqrt{sin^2x+\left(2m-3\right)cosx+3m-2}}\). Có bao nhiêu giá trị của m thuộc khoảng (-2023;2023) để hàm số xác định với mọi x thuộc R
Hàm số xác định trên R khi và chỉ khi:
\(sin^2x+\left(2m-3\right)cosx+3m-2>0;\forall x\in R\)
\(\Leftrightarrow-cos^2x+\left(2m-3\right)cosx+3m-1>0\)
\(\Leftrightarrow t^2-\left(2m-3\right)t-3m+1< 0;\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow t^2+3t+1< m\left(2t+3\right)\)
\(\Leftrightarrow\dfrac{t^2+3t+1}{2t+3}< m\) (do \(2t+3>0;\forall t\in\left[-1;1\right]\))
\(\Leftrightarrow m>\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}\)
Ta có: \(\dfrac{t^2+3t+1}{2t+3}=\dfrac{t^2+t-2+2t+3}{2t+3}=\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}+1\)
Do \(-1\le t\le1\Rightarrow\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}\le0\)
\(\Rightarrow\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}=1\)
\(\Rightarrow m>1\)
Đúng 2
Bình luận (1)