Câu 5a,b ạ:(((
TH
Những câu hỏi liên quan
rút gọn :
(3a+4)^2+(4a-1)^2+(2+5a)(2-5a)
OMG CÂU DƯỚI SAI ĐỀ Ạ LÀM CÂU NÀY Ạ
\(\left(3a+4\right)^2+\left(4a-1\right)^2+\left(2+5a\right)\left(2-5a\right)=9a^2+24a+16+16a^2-8a+1+4-25a^2=16a+21\)
Đúng 1
Bình luận (0)
Dạ thầy cô và các bạn chỉ em câu a4,4b,4c,4d và câu 5a với ạ
Em cảm ơn ạ
4a.
\(y'=\dfrac{1}{cos^2x}+cosx-2=\dfrac{cos^3x-2cos^2x+1}{cos^2x}=\dfrac{\left(1-cosx\right)\left(1+cosx\left(1-cosx\right)\right)}{cos^2x}>0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm đồng biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
4b.
\(y'=-sinx-1\le0\) ; \(\forall x\in\left(0;2\pi\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;2\pi\right)\)
c.
\(y'=-sinx-\dfrac{1}{sin^2x}+2=\dfrac{-sin^3x+2sin^2x-1}{sin^2x}=\dfrac{\left(sinx-1\right)\left(1-sin^2x+sinx\right)}{sin^2x}\)
\(=\dfrac{\left(sinx-1\right)\left(cos^2x+sinx\right)}{sin^2x}< 0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
Đúng 1
Bình luận (0)
4d.
\(y=cosx+sinx.cosx=cosx+\dfrac{1}{2}sin2x\)
\(y'=-sinx+cos2x=-sinx+1-2sin^2x\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{3\pi}{2}\right\}\)
Bảng biến thiên
Từ BBt ta thấy hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{5\pi}{6};2\pi\right)\)
Hàm nghịch biến trên \(\left(\dfrac{\pi}{6};\dfrac{5\pi}{6}\right)\)
Đúng 1
Bình luận (0)
5a.
\(y'=x^2-4x+m\)
Hàm đồng biến trên TXĐ khi và chỉ khi \(y'\ge0\) ; \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=4-m\le0\end{matrix}\right.\)
\(\Leftrightarrow m\ge4\)
Đúng 1
Bình luận (0)
giúp mik lm câu này vs ạ
f(x) = x4 – 3x2 + x – 1
g(x) = x4 – x3 + x2 + 5
a) f(x)+g(x)
b)f(x)-g(x)
a) f(x)+g(x) = 2x4 -x3 -2x2+x+4
b) f(x)-g(x) =x3-4x2+x-5
Đúng 0
Bình luận (0)
Giải thích các bước giải:
a) f(x)+g(x)=x4x4 – 3x23x2 + x – 1 + x4x4 - x3x3 + x2x2 + 5
=2x42x4 - x3x3 -2x22x2 +x +4
b)f(x)-g(x)=x4x4 – 3x23x2 + x – 1 - x4x4 + x3x3 - x2x2 - 5
= x3x3 - 4x24x2 +x -6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giải giùm em câu 5a ạ

Câu 5b)
T = lx - 1l + lx + 2l + lx - 3l + lx + 4l + lx - 5l + lx + 6l + lx - 7l + lx + 8l + lx - 9l
Vì lx - 1l; lx + 2l; lx - 3l; lx + 4l; lx - 5l; lx + 6l; lx - 7l; lx + 8l; lx - 9l luôn \(\ge\)0 với mọi x
\(\Rightarrow\)lx - 1l + lx + 2l + lx - 3l + lx + 4l + lx - 5l + lx + 6l + lx - 7l + lx + 8l + lx - 9l\(\ge\)0 + 0 + 0 + .... + 0 = 0
\(\Rightarrow T\ge0\)với mọi x
\(\Rightarrow Min\)\(T=0\)\(\Leftrightarrow x\in\left\{1;-2;3;-4;5;-6;7;-8;9\right\}\)
Vậy giá trị nhỏ nhất của T = 0 \(khix\in\left\{1;-2;3;-4;5;-6;7;-8;9\right\}\)
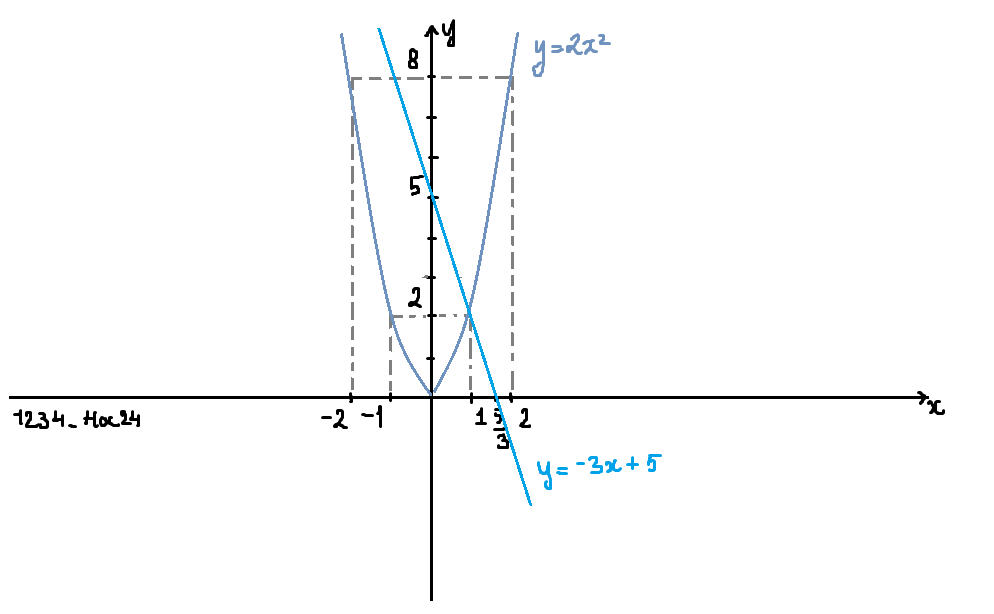
Cho Parabol (P): y = 2x2 và đường thẳng (d): y = -3x+5
a)Vẽ đồ thị hai hàm số trên cùng một mặt phẳng toạ độ.
Ai biết câu này ko ạ
\(\left(P\right):y=2x^2\)
\(BGT:\)
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(y=2x^2\) | \(8\) | \(2\) | \(0\) | \(2\) | \(8\) |
\(\left(d\right):y=-3x+5\)
\(BGT:\)
| \(x\) | \(0\) | \(\dfrac{5}{3}\) |
| \(y=-3x+5\) | \(5\) | \(0\) |
Đúng 0
Bình luận (0)
Cho biết a+b = 5 . Tính các tổng
a) 5a+16b+4b+15a
b) 13a+5b+13b+5a
. Ai giải được hậu tạ ạ ^^
a. 5a+16b+4b+15a= (5a+15a) + (16b+4b)
= 20a + 20b = 20(a+b) = 20 * 5 = 100
b. 13a+5b+13b+5a = (13a+5a) + (5b+13b)
= 18a + 18b = 18(a+b) = 18*5 = 90
Đúng 0
Bình luận (0)
Cho biết a+b = 5 . Tính các tổng
a) 5a+16b+4b+15a
b) 13a+5b+13b+5a
. Ai giải được hậu tạ ạ ^^
mình chỉ biết câu a thôi
a)13a+5b+13b+5a
=13(a+b)+5(a+b)
=(13+5)(a+b)
=18.5=90
Đúng 0
Bình luận (0)
a)5a+16b+4b+15a
=a(5+15)+b(16+4)
=20a+20b
=20(a+b)
=20.5
=100
Đúng 0
Bình luận (0)
Tìm các số ạ, b biết
|5a-6b+300|^2007+(2a-3b)^2008=0
Vì \(\left|5a-6b+300\right|\ge0\forall a;b\Rightarrow\left|5a-6b+300\right|^{2007}\ge0\forall a;b\)
và \(\left(2a-3b\right)^{2008}\ge0\forall a;b\)
Mà tổng của chúng bằng 0
\(\Rightarrow\hept{\begin{cases}5a-6b+300=0\\2a-3b=0\end{cases}}\)
\(2a-3b=0\Leftrightarrow2a=3b\)
\(\Leftrightarrow5a-6b+300=0\)
\(\Leftrightarrow5a-2\cdot2a+300=0\)
\(\Leftrightarrow5a-4a=-300\)
\(\Leftrightarrow a=-300\)
\(\Rightarrow2a-3b=2\cdot\left(-300\right)-3b=0\)
\(\Leftrightarrow-600-3b=0\)
\(\Leftrightarrow-3b=600\)
\(\Leftrightarrow b=-200\)
Vậy a = -300 và b = -200
Đúng 0
Bình luận (0)
Cho 5a+2b = 65 và 2a+11b = 26, tìm a và b.
Giúp mình với ạ
\(\hept{\begin{cases}5a+2b=65\left(1\right)\\2a+11b=26\left(2\right)\end{cases}\hept{\begin{cases}20a+8b=260\\20a+110b=260\end{cases}}}\)
dễ thấy \(102b=0\)
\(b=0\) thế vào (1)
\(5a+0=65\)
\(a=13\)
\(\hept{\begin{cases}b=0\\a=13\end{cases}}\)



