Huhu cao nhân giúp em với em đang thi:(( 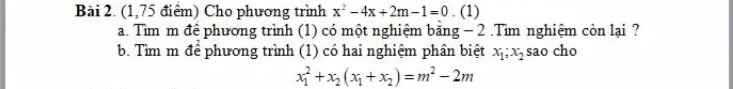
NT
Những câu hỏi liên quan
Nốt câu c giúp em với các cao nhân ơi huhu"))))
Mọi người ơi, giúp em với ạ. Em đang cần gấp lắm ạ ;-; huhu giúp em với
Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)
Đúng 0
Bình luận (0)
giúp em với em đang cần gấp huhu
giúp em với em đang cần gấp lắm mọi người ơi huhu
1.
a.
\(n^2+7n+1=k^2\Rightarrow4n^2+28n+4=4k^2\)
\(\Leftrightarrow\left(2n+7\right)^2-45=\left(2k\right)^2\)
\(\Leftrightarrow\left(2n-2k+7\right)\left(2n+2k+7\right)=45\)
Phương trình ước số cơ bản
b.
\(a^3b^3+b^3-3ab^2=-1\)
\(\Leftrightarrow a^3+1-\dfrac{3a}{b}=-\dfrac{1}{b^3}\)
\(\Leftrightarrow a^3+\dfrac{1}{b^3}+1-\dfrac{3a}{b}=0\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x^3+y^3+1-3xy=0\)
\(\Leftrightarrow\left(x+y\right)^3+1-3xy\left(x+y\right)-3xy=0\)
\(\Leftrightarrow\left(x+y+1\right)\left(x^2+y^2+1-xy-x-y\right)=0\)
\(\Leftrightarrow x+y+1=0\)
\(\Rightarrow P=a+\dfrac{1}{b}=x+y=-1\)
Đúng 0
Bình luận (0)
2.
a.
\(a+b+\dfrac{1}{a}+\dfrac{1}{b}=\left(\dfrac{a}{4}+\dfrac{1}{a}\right)+\left(\dfrac{b}{4}+\dfrac{1}{b}\right)+\dfrac{3}{4}\left(a+b\right)\)
\(\ge2\sqrt{\dfrac{a}{4a}}+2\sqrt{\dfrac{b}{4b}}+\dfrac{3}{4}.4=5\) (đpcm)
Dấu "=" xảy ra khi \(a=b=2\)
Đúng 0
Bình luận (0)
2.b
b.
\(\Leftrightarrow x^4+4x+4=y^4+4y+4\)
\(\Leftrightarrow\left(x+2\right)^2=y^4+4y+4\)
\(\Rightarrow y^4+4y+4\) là số chính phương
Ta có: \(y^4+4y+4>y^4\) với mọi y nguyên dương
\(y^4+4y+4\le y^4+4y^2+4=\left(y^2+2\right)^2\)
\(\Rightarrow\left(y^2\right)^2< y^4+4y+4\le\left(y^2+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}y^4+4y+4=\left(y^2+1\right)^2\\y^4+4y+4=\left(y^2+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2y^2-4y-3=0\left(ktm\right)\\y^2-y=0\Rightarrow y=1\end{matrix}\right.\)
Thế vào pt ban đầu \(\Rightarrow x^2+4x=5\Rightarrow x=1\)
Vậy \(\left(x;y\right)=\left(1;1\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp em với QTV ơi huhu em đang cần gấp lắm ạ TT
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)
Đúng 0
Bình luận (1)
Mọi người giúp em với huhu em đang cần gấp ạ :))
Xem thêm câu trả lời
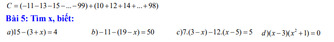 mọi người ơi, giúp em với sắp thi roii huhu
mọi người ơi, giúp em với sắp thi roii huhu
Bài 5 :
a, \(x+3=1\Leftrightarrow x=-2\)
b, \(19-x=-61\Leftrightarrow x=80\)
c, \(21-7x-12x+60=5\Leftrightarrow-19x=-76\Leftrightarrow x=4\)
d, \(\left(x-3\right)\left(x^2+1>0\right)=0\Leftrightarrow x=3\)
Đúng 0
Bình luận (2)
Giúp em với ạ❤❤❤❤. Em đang cần gấp lắm ạ. Huhu
Huhu các cao nhân giúp mình với mình đang cần gấp, mình cảm ơn ạ. Nếu được câu giải chi tiết cho mình với :((((((.
a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)
Đúng 1
Bình luận (0)





