Ai giải giúp câu 2

KG
Những câu hỏi liên quan
Ai giải giúp em 2 câu còn lại câu 3 và câu 4 ạ
Ai giúp tuii giải câu 2 với nhaa
Ai giải giúp mik câu 2 vs ạ
Câu 2:
Gọi số sách Nam mua được là x(sách)(Điều kiện: \(x\in Z^+\))
Số tập Nam mua được là: x+3(tập)
Theo đề, ta có phương trình:
\(12000x+5000\left(x+3\right)=83000\)
\(\Leftrightarrow12000x+5000x+15000=83000\)
\(\Leftrightarrow17000x=68000\)
hay x=4(thỏa ĐK)
Vậy: Bạn Nam mua được 4 quyển sách và 7 cuốn tập
Đúng 0
Bình luận (0)
ai giải giúp tui 2 câu này với
Bài 4:
Ta có: Góc A và góc O là hai trong cùng phía => Ax// Oz (1)
Góc O và góc B là hai góc trong cùng phía => Oz// By (1)
Từ (1 ) và (2 ) => Az// By
Mình chỉ biết vậy thoi, có j sai thì xin lỗi nhaa
Đúng 0
Bình luận (1)
Bài 4
Kéo dài Oz ra rồi tìm góc SLT-> chứng minh là xong
Đúng 0
Bình luận (1)
ai giải hộ e 2 câu này với ạ .nhanh giúp e với

Ai giải giúp mk 2 câu đấy phần b với lại chỗ 2, thui với ạ!

1.
a, \(\left(C\right)x^2+y^2-6x-2y+6=0\)
\(\Leftrightarrow\left(C\right)\left(x-3\right)^2+\left(y-1\right)^2=4\)
\(\Rightarrow\) Tâm \(I=\left(3;1\right)\), bán kính \(R=2\)
b, Tiếp tuyến đi qua A có dạng: \(\left(\Delta\right)ax+by-5a-7b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|3a+b-5a-7b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+3b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow6ab+8b^2=0\)
\(\Leftrightarrow2b\left(3a+4b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}b=0\\3a+4b=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
TH1: \(\Delta_1:x=5\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x=5\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y^2-2y+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\Rightarrow\left(5;1\right)\)
TH2: \(\Delta_2:4x-3y+1=0\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}4x-3y+1=0\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{5}\\y=\dfrac{11}{5}\end{matrix}\right.\Rightarrow\left(\dfrac{7}{5};\dfrac{11}{5}\right)\)
Kết luận: Phương trình tiếp tuyến: \(\left\{{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
Tọa độ tiếp điểm: \(\left\{{}\begin{matrix}\left(5;1\right)\\\left(\dfrac{7}{5};\dfrac{11}{5}\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Các bạn ơi! Ai giúp giải 2 câu này với, mình cảm ơn nhiều.🌻
giúp em câu 6 câu 7 với câu 7 ai có thể giải thích giúp em không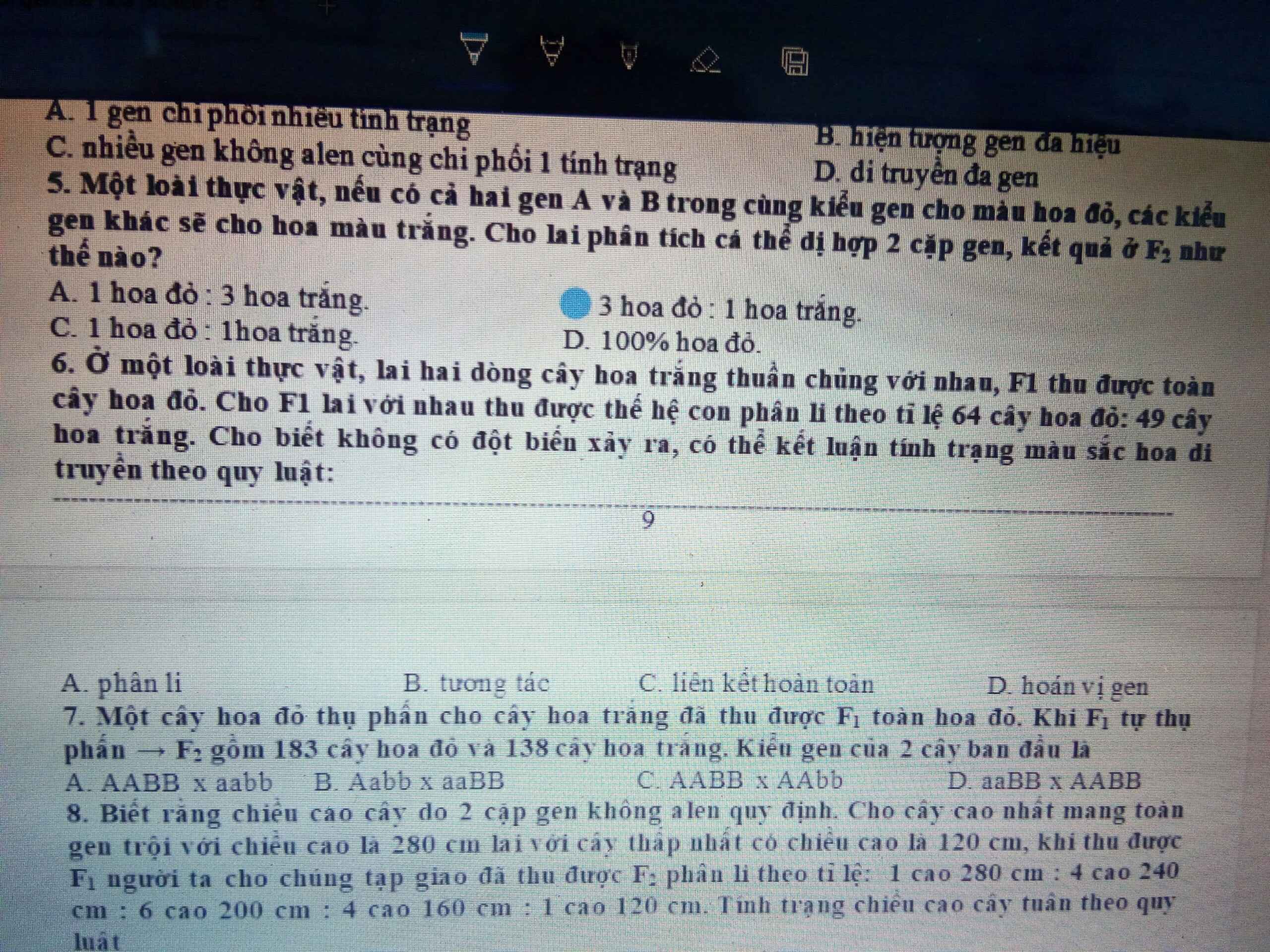
ai giải giúp mình câu này với : -5/7- | 1/2-x| = -11/4
\(\Leftrightarrow\frac{5}{7}+\left|\frac{1}{2}-x\right|=\frac{11}{4}\)
\(\Leftrightarrow\left|\frac{1}{2}-x\right|=\frac{11}{4}-\frac{5}{7}=\frac{77-20}{28}=\frac{57}{28}\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}-x=\frac{57}{28}\\\frac{1}{2}-x=-\frac{57}{28}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}-\frac{57}{28}=\frac{14-57}{28}=\frac{-43}{28}\\x=\frac{1}{2}+\frac{57}{28}=\frac{14+57}{28}=\frac{71}{28}\end{cases}}\)
PT có 2 nghiệm là: -43/28 và 71/28
Đúng 0
Bình luận (0)
TH1 : \(x< \frac{1}{2}\), ta có:
\(-\frac{5}{7}-\left(\frac{1}{2}-x\right)=-\frac{11}{4}\)
\(-\frac{5}{7}-\frac{1}{2}+x=-\frac{11}{4}\)
\(-\frac{17}{14}+x=-\frac{11}{4}\)
\(x=-\frac{11}{4}-\left(-\frac{17}{14}\right)\)
\(x=-\frac{43}{28}\)( thỏa mãn )
TH2 : \(x\ge\frac{1}{2}\); ta có:
\(-\frac{5}{7}-\left(x-\frac{1}{2}\right)=-\frac{11}{4}\)
\(-\frac{5}{7}-x+\frac{1}{2}=-\frac{11}{4}\)
\(-\frac{3}{14}-x=-\frac{11}{4}\)
\(x=-\frac{3}{14}-\left(-\frac{11}{4}\right)\)
\(x=\frac{71}{28}\)(thỏa mãn)
Vậy \(\orbr{\begin{cases}x=\frac{-43}{28}\\x=\frac{71}{28}\end{cases}}\)
Đúng 0
Bình luận (0)



