tìm a và b biết ( 50a + 7b + 3 )( 50 mũ a + 50a + b ) bằng 803
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NT
Những câu hỏi liên quan
Tìm các số tự nhiên a,b thoả mãn:(50a+7b+3).(\(50^a\)+50a+b)=803
ngocduong516
06/12/2021
ta có : 803 là số lẻ
=> ( 50a + 7b + 3 )( 50^a + 50a + b ) là số lẻ
=> 50a + 7b + 3 và 50^a + 50a + b là số lẻ
TH1 : nếu a khác 0
=> 50^a + 50a là là số chẵn
mà 50^a + 50a + b là số lẻ ( theo trên )
=> b lẻ
=> 50b + 3 chẵn
=> 50a + 7b + 3 chẵn ( loại )
TH2 : a = 0
=> (7b+3)(b+1) = 803 = 1. 803 = 11.73
vì b thuộc N
=> 7b + 3 > b+1
do đó
7b + 3 = 803 và b +1 = 1 => loại
hoặc 7b+3 = 73 và b +1 = 11 => b = 50
vậy a = 0 và b = 100
Đúng 1
Bình luận (0)
cho tam giác ABC=tam giác PQR.Biết A=50 và B-C=50
a)chứng minh rằng tam giác PQR là tam giác vuông
b)Chỉ ra các cặp cạnh bằng nhau của hai tam giác
Mọi người giúp mình với ![]()
Giải:
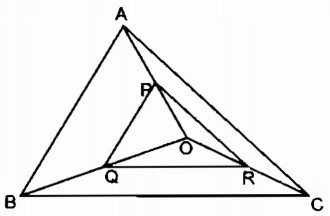
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Suy ra: PQ=12ABPQ=12AB
(tính chất đường trung bình của tam giác )
Suy ra: PQAB=12PQAB=12 (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: PR=12ACPR=12AC (tính chất đường trung bình của tam giác )
Suy ra: PRAC=12PRAC=12 (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: QR=12BCQR=12BC (tính chất đường trung bình của tam giác )
Suy ra: QRBC=12QRBC=12 (3)
Từ (1), (2) và (3) suy ra: PQAB=PRAC=QRBC=12PQAB=PRAC=QRBC=12
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: PQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′pPQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′p
Vậy: p′p=12⇒p′=12p=12.543=271,5p′p=12⇒p′=12p=12.543=271,5 (cm)
Đúng 1
Bình luận (2)
giúp mik với
vd chọn 50 a thì các bạn nhắn 50a!
Xem thêm câu trả lời
cho tam giác abc vuông tại a đường cao ah. biết AH = 24a , BC = 50a và AB < Ac . tính ab , ac
cho tam giác ABC vuông tại A, đường cao AH. Biết AH=2a, BC=50a và AB<AC. Tính AB, AC
khai phương các tích sau:
A = \(\sqrt{50a^5b^7}\) với (a, b > 0)
B = \(\sqrt{\dfrac{1}{4}\left(x-1\right)^2x^4}\)
a: \(=5\sqrt{2}\cdot a^2\cdot b^3\cdot\sqrt{ab}\)
b: \(=\dfrac{1}{2}\cdot x^2\cdot\left|x-1\right|\)
Đúng 1
Bình luận (0)
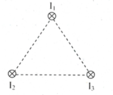
Ba dây dẫn thẳng dài và song song cách đều nhau một khoảng a 20 cm (hình vẽ). Cường độ dòng điện chạy trong 3 dây lần lượt là I1 50A, I2 I3 20A.Xác định phương chiều và độ lớn của lực từ tác dụng lên 1m của dây 1 bằng 2 cách: a) Dựa vào cảm ứng từ B vừa tính câu a. b) Tính trực tiếp
Đọc tiếp
Ba dây dẫn thẳng dài và song song cách đều nhau một khoảng a = 20 cm (hình vẽ). Cường độ dòng điện chạy trong 3 dây lần lượt là I1 = 50A, I2 = I3 = 20A.
Xác định phương chiều và độ lớn của lực từ tác dụng lên 1m của dây 1 bằng 2 cách:
a) Dựa vào cảm ứng từ B vừa tính câu a.
b) Tính trực tiếp
Rút gọn biểu thức:
\(M=\left(\frac{\sqrt{50a}}{\sqrt{a}-\sqrt{b}}+\frac{\sqrt{20b}}{\sqrt{b}-\sqrt{a}}\right).\frac{a-b}{\sqrt{a}+\sqrt{b}}\)
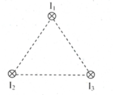
Ba dây dẫn thẳng dài và song song cách đều nhau một khoảng a = 20 cm (hình vẽ). Cường độ dòng điện chạy trong 3 dây lần lượt là I1 = 50A, I2 = I3 = 20A. Xác định cảm ứng từ B tại điểm cách dây 2 và dây 3 một khoảng a = 20 cm (tại I1)