Giải:
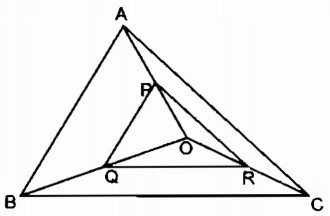
a. Trong tam giác AOB, ta có:
P trung điểm của OA (gt)
Q trung điểm của OB (gt)
Suy ra: PQ là đường trung bình của ∆ OAB.
Suy ra: PQ=12ABPQ=12AB
(tính chất đường trung bình của tam giác )
Suy ra: PQAB=12PQAB=12 (1)
Trong tam giác OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra: PR là đường trung bình của tam giác OAC.
Suy ra: PR=12ACPR=12AC (tính chất đường trung bình của tam giác )
Suy ra: PRAC=12PRAC=12 (2)
Trong tam giác OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra: QR là đường trung bình của tam giác OBC.
Suy ra: QR=12BCQR=12BC (tính chất đường trung bình của tam giác )
Suy ra: QRBC=12QRBC=12 (3)
Từ (1), (2) và (3) suy ra: PQAB=PRAC=QRBC=12PQAB=PRAC=QRBC=12
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c)
b. Gọi p’ là chu vi tam giác PQR.
Ta có: PQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′pPQAB=PRAC=QRBC=PQ+PR+QRAB+AC+BC=p′p
Vậy: p′p=12⇒p′=12p=12.543=271,5p′p=12⇒p′=12p=12.543=271,5 (cm)