cho tam giác ABC có AB= 6cm, AC= 5cm, BC=9cm. Điểm D thuộc cạnh BC sao cho BD= 4cm. Tính độ dài AD
1K
Những câu hỏi liên quan
cho tam giác ABC có AB = 9cm; điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE//BC (E thuộc AC) , Kẻ EF//CD ( F thuộc AB ). Độ dài cạnh AF là ... cm :))
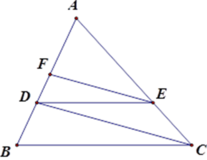
Cho tam giác ABC có AB = 9cm; điểm D thuộc cạnh AB sao cho AD = 6cm.
Kẻ DE // BC (E thuộc AC), kẻ EF // AD (F thuộc AB).
Độ dài cạnh AF là ............... cm.
Cho tam giác ABC có độ dài ba cạnh là: AB=9cm, AC=12cm, BC=6cm. Trên AB lấy điểm D sao cho AD=4cm, trên AC lấy điểm E sao cho AE=3cm. a) CM tam giác AED và tam giác ACB đồng dạng b) Gọi F là giao điểm của ED và BC. Tính FB, FD . (^•^, Các bạn giúp mình với nha,^•^)
Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
A. 6 cm
B. 5 cm
C. 4 cm
D. 7 cm
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , AC=20cm, AB=15cm
a. Lấy điểm D trên cạnh BC sao cho AD=AB. tính độ dài BD
b. Lấy điểm D trên cạnh BC sao cho BD=4cm . Tính độ dài AD
Bài 1 : Cho tan giác ABC cân tại A ,dường cai Ah9cm và BC24cm.a)Tính độ dài AB,AC ?b)Trên CB lấy điểm M sa cho CM5cm ,trên CA lấy điểm Nsao cho CN8cm.Chứng minh tam giác CMN đồng dạng với tam giác CAB c)MN kéo dài cắt BA tại I . Chứng minh IA.IBIM.INBài 2 : Cho tam giác ABC có AB12cm;BC9cm;AC10cm;trên tia đối của tia AB, AC lần lượt lấy các điểm D,E sao cho AD5cm,AE6cm a)chứng minh tam giác ABC và tam giác AED đồng dạng b)tính độ dài đoạn thẳng EDc)gọi M là giao điểm của BE và CD chứng minh MB.M...
Đọc tiếp
Bài 1 : Cho tan giác ABC cân tại A ,dường cai Ah=9cm và BC=24cm.
a)Tính độ dài AB,AC ?
b)Trên CB lấy điểm M sa cho CM=5cm ,trên CA lấy điểm Nsao cho CN=8cm.Chứng minh tam giác CMN đồng dạng với tam giác CAB
c)MN kéo dài cắt BA tại I . Chứng minh IA.IB=IM.IN
Bài 2 : Cho tam giác ABC có AB=12cm;BC=9cm;AC=10cm;trên tia đối của tia AB, AC lần lượt lấy các điểm D,E sao cho AD=5cm,AE=6cm
a)chứng minh tam giác ABC và tam giác AED đồng dạng
b)tính độ dài đoạn thẳng ED
c)gọi M là giao điểm của BE và CD chứng minh MB.ME=MC.MD
Bài 3 : cho tam giác ABC có AB=6m;BC=10cm;AC=9cm;trên tia AC lấy điểm D sao cho AD=4cm
a)chứng minh tam giác ABC và tam giác ADB đồng dạng
b)tính độ dài đoạn thẳng DB
c)Kẻ DE song song với AB (E thuộc BC ) Chứng minh BD2=BC.BE
Bài 8:
Cho tam giác ABC có AB= 9cm, BC= 15cm, AC=12cm. D là điểm trên cạnh AC sao cho AD= 2cm. Tính độ dài đoạn thẳng BD. ( cần hình )
Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
\(BD=\sqrt{2^2+9^2}=\sqrt{85}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=4cm, AC=5cm, BC=6cm, các đường phân giác BD và cắt nhau ở I.
a) Tính các độ dài AD, DC.
b) Tính các độ dài AE, BE.
Sửa đề: Các đường phân giác BD và CE cắt nhau ở I
a.Áp dụng t/c đường phân giác góc B, ta có:
\(\dfrac{AB}{BC}=\dfrac{AD}{CD}\)
\(\Leftrightarrow\dfrac{4}{6}=\dfrac{AD}{CD}\) \(\Leftrightarrow\dfrac{2}{3}=\dfrac{AD}{CD}\) \(\Leftrightarrow\dfrac{CD}{3}=\dfrac{AD}{2}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{CD}{3}=\dfrac{AD}{2}=\dfrac{CD+AD}{3+2}=\dfrac{AC}{5}=\dfrac{5}{5}=1\)
\(\Rightarrow CD=1.3=3cm\)
\(\Rightarrow AD=1.2=2cm\)
b.Áp dụng t/c đường phân giác góc C, ta có:
\(\dfrac{CA}{CB}=\dfrac{AE}{BE}\)
\(\Leftrightarrow\dfrac{5}{6}=\dfrac{AE}{BE}\)\(\Leftrightarrow\dfrac{BE}{6}=\dfrac{AE}{5}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{BE}{6}=\dfrac{AE}{5}=\dfrac{BE+AE}{6+5}=\dfrac{AB}{11}=\dfrac{4}{11}\)
\(\Rightarrow BE=\dfrac{4}{11}.6=\dfrac{24}{11}cm\)
\(\Rightarrow AE=\dfrac{4}{11}.5=\dfrac{20}{11}cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=6cm, AC = 8 cm. Độ dài của BC là?
A. BC = 4cm B. BC = 5cm C. BC = 9cm D. BC = 10cm







