Rút gọn biểu thức \(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
ND
Những câu hỏi liên quan
Rút gọn biểu thức
\(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}-3\sqrt{5\sqrt{48}}}\)
\(2\sqrt{5\sqrt{3}}-2\sqrt{8\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
Help me plsssssss
Help me plssssssss
a: \(=2\sqrt{20\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\cdot\sqrt{20\sqrt{3}}\)
\(=4\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}=-4\sqrt{5\sqrt{3}}\)
b: \(=2\sqrt{5\sqrt{3}}-4\sqrt{2\sqrt{3}}-6\sqrt{5\sqrt{3}}=-4\sqrt{5\sqrt{3}}-4\sqrt{2\sqrt{3}}\)
Đúng 1
Bình luận (1)
Rút gọn biểu thức: \(\frac{\sqrt{20+8\sqrt{3}} +\sqrt{20-8\sqrt{3}}}{\sqrt{5+2\sqrt{3}}-\sqrt{5-2\sqrt{3}}}-\frac{\sqrt{4+\sqrt{3}}+\sqrt{4-\sqrt{3}}}{\sqrt{4+\sqrt{3}}-\sqrt{4-\sqrt{3}}}\)
1) Rút gọn các biểu thức sau:a) sqrt[3]{27} - sqrt[3]{-8} - sqrt[3]{125}b) sqrt{20} - sqrt{45} + 3sqrt{18} + sqrt{72}c) 2sqrt{5} + sqrt{left(1-sqrt{5}right)^2} d) dfrac{1}{sqrt{3}+1} + dfrac{1}{sqrt{3}-1} - 2sqrt{3}e) dfrac{a-b}{sqrt{a}-sqrt{b}} - dfrac{sqrt{a^3}-sqrt{b^3}}{a-b} với a ≥ 0 , b≥0 , a ≠ b
Đọc tiếp
1) Rút gọn các biểu thức sau:
a) \(\sqrt[3]{27}\) - \(\sqrt[3]{-8}\) - \(\sqrt[3]{125}\)
b) \(\sqrt{20}\) - \(\sqrt{45}\) + 3\(\sqrt{18}\) + \(\sqrt{72}\)
c) 2\(\sqrt{5}\) + \(\sqrt{\left(1-\sqrt{5}\right)^2}\)
d) \(\dfrac{1}{\sqrt{3}+1}\) + \(\dfrac{1}{\sqrt{3}-1}\) - 2\(\sqrt{3}\)
e) \(\dfrac{a-b}{\sqrt{a}-\sqrt{b}}\) - \(\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\) với a ≥ 0 , b≥0 , a ≠ b
Rút gọn biểu thức :
a) A=\(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\).
b)B=\(\sqrt[3]{20+14\sqrt{2}}+\sqrt[3]{20-14\sqrt{2}}\)
c) C=\(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}.\)
a) Ta có: \(A^3=\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)^3\)
\(=2+\sqrt{5}+2-\sqrt{5}+3\cdot\sqrt[3]{\left(2+\sqrt{5}\right)\left(2-\sqrt{5}\right)}\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)\)
\(=4-3\cdot A\)
\(\Leftrightarrow A^3+3A-4=0\)
\(\Leftrightarrow A^3-A+4A-4=0\)
\(\Leftrightarrow A\left(A-1\right)\left(A+1\right)+4\left(A-1\right)=0\)
\(\Leftrightarrow\left(A-1\right)\left(A^2+A+4\right)=0\)
\(\Leftrightarrow A=1\)
Đúng 3
Bình luận (0)
Rút gọn biểu thức :
a) \(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
b) \(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
a) \(2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
\(=2\sqrt{40.2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{5.4\sqrt{3}}\)
\(=\left(2\sqrt{80}-2\sqrt{5}-3\sqrt{20}\right).\sqrt{\sqrt{3}}\)
\(=\left(8\sqrt{5}-2\sqrt{5}-6\sqrt{5}\right).\sqrt{\sqrt{3}}=0\)
b) \(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
\(=\left(4\sqrt{2}-2\sqrt{5}-6\sqrt{5}\right).\sqrt{\sqrt{3}}\)
\(=\left(4\sqrt{2}-8\sqrt{5}\right).\sqrt{\sqrt{3}}\)
\(=\sqrt{\sqrt{3}}\left(\sqrt{2}-2\sqrt{5}\right)\)
Đúng 0
Bình luận (1)
a)2\(\sqrt{40\sqrt{12}}\) -2\(\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
=\(2\sqrt{40.2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
=\(2\sqrt{80\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
=\(8\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}\)
=0
b)\(2\sqrt{8\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
=\(4\sqrt{2\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}\)
=4\(\sqrt{2\sqrt{3}}-8\sqrt{5\sqrt{3}}\)
Rút gọn biểu thức sau: \(\sqrt{9-3\sqrt{8}}\) - \(\dfrac{\sqrt{3}-1}{\sqrt{2}}\) + \(\sqrt{5-2\sqrt{6}}\) - \(\sqrt{2-\sqrt{3}}\)
\(\sqrt{9-3\sqrt{8}}-\dfrac{\sqrt{3}-1}{\sqrt{2}}+\sqrt{5-2\sqrt{6}}-\sqrt{2-\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{6}\right)^2-2.\sqrt{6}.\sqrt{3}+\left(\sqrt{3}\right)^2}-\dfrac{\sqrt{6}-\sqrt{2}}{2}+\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.\sqrt{2}+\left(\sqrt{2}\right)^2}-\dfrac{\sqrt{6}-\sqrt{2}}{2}\)
\(=\sqrt{\left(\sqrt{6}-\sqrt{3}\right)^2}-\sqrt{6}+\sqrt{2}+\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{6}-\sqrt{3}\right|-\sqrt{6}+\sqrt{2}+\left|\sqrt{3}-\sqrt{2}\right|\)
\(=\sqrt{6}-\sqrt{3}-\sqrt{6}+\sqrt{2}+\sqrt{3}-\sqrt{2}\) (do \(\sqrt{6}-\sqrt{3}>0;\sqrt{3}-\sqrt{2}>0\))
\(=0\)
Đúng 1
Bình luận (0)
\(=\sqrt{9-6\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{2}}{2}+\sqrt{3}-\sqrt{2}-\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1\right)\)
\(=\sqrt{6}-\sqrt{3}-\dfrac{1}{2}\sqrt{6}+\dfrac{1}{2}\sqrt{2}+\sqrt{3}-\sqrt{2}-\dfrac{1}{2}\sqrt{6}+\dfrac{1}{2}\sqrt{2}\)
\(=0\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau
\(a.\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}\)
\(b.\dfrac{\sqrt{\dfrac{5}{3}}+\sqrt{\dfrac{3}{5}}-2}{\sqrt{\dfrac{5}{3}}-\sqrt{\dfrac{3}{5}}}\)
a: \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}\)
\(=\dfrac{\sqrt{2}+\sqrt{3}+2}{\sqrt{2}+\sqrt{3}+2+2+\sqrt{6}+\sqrt{8}}\)
\(=\dfrac{1}{\sqrt{2}+1}=\sqrt{2}-1\)
Đúng 2
Bình luận (0)
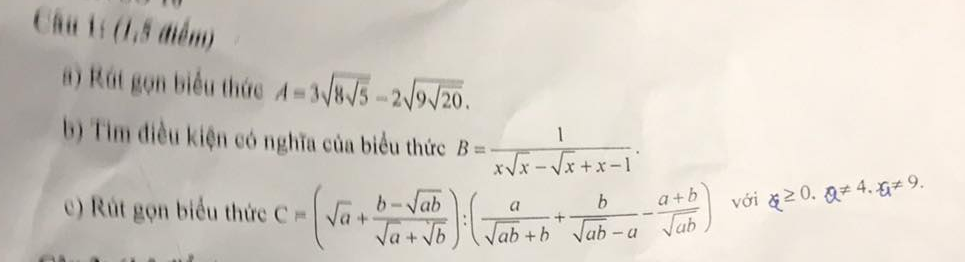
c1
a. rút gọn biểu thức
\(A=3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\)
b. tìm đk có nghĩa của biểu thức
\(B=\dfrac{1}{x\sqrt{x}-\sqrt{x}+x-1}\)
`#Hưng`
\(a,3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\\ =\sqrt{9.8\sqrt{5}}-\sqrt{4.9\sqrt{20}}\\ =\sqrt{72\sqrt{5}}-\sqrt{36\sqrt{20}}\\ =\sqrt{\sqrt{5184.5}}-\sqrt{\sqrt{1296.20}}\\ =\sqrt{\sqrt{25920}}-\sqrt{\sqrt{25920}}\\ =0\)
\(b,ĐKXĐ:x\sqrt{x}-\sqrt{x}+x-1\ne0\\ \Rightarrow\sqrt{x}\left(x-1\right)+\left(x-1\right)\ne0\\ \Rightarrow\left(x-1\right)\left(\sqrt{x}+1\right)\ne0\\ \Rightarrow x-1\ne0\left(vì.\sqrt{x}+1>0\right)\\ \Rightarrow x\ne1\)
Đúng 1
Bình luận (1)
rút gọn các biểu thức sau:
a \(\sqrt[3]{8\sqrt{5}-16}.\sqrt[3]{8\sqrt{5}+16}\)
b \(\sqrt[3]{7-5\sqrt{2}}-\sqrt[6]{8}\)
c \(\sqrt[3]{4}.\sqrt[3]{1-\sqrt{3}}.\sqrt[6]{4+2\sqrt{3}}\)
d \(\dfrac{2}{\sqrt[3]{3}-1}-\dfrac{4}{\sqrt[3]{9}-\sqrt[3]{3}+1}\)
`c)root{3}{4}.root{3}{1-sqrt3}.root{6}{(sqrt3+1)^2}`
`=root{3}{4(1-sqrt3)}.root{3}{1+sqrt3}`
`=root{3}{4(1-sqrt3)(1+sqrt3)}`
`=root{3}{4(1-3)}=-2`
`d)2/(root{3}{3}-1)-4/(root{9}-root{3}{3}+1)`
`=(2(root{3}{9}+root{3}{3}+1))/(3-1)-(4(root{3}{3}+1))/(3+1)`
`=root{3}{9}+root{3}{3}+1-root{3}{3}-1`
`=root{3}{9}`
Đúng 3
Bình luận (1)
`a)root{3}{8sqrt5-16}.root{3}{8sqrt5+16}`
`=root{3}{(8sqrt5-16)(8sqrt5+16)}`
`=root{3}{320-256}`
`=root{3}{64}=4`
`b)root{3}{7-5sqrt2}-root{6}{8}`
`=root{3}{1-3.sqrt{2}+3.2.1-2sqrt2}-root{6}{(2)^3}`
`=root{3}{(1-sqrt2)^3}-sqrt2`
`=1-sqrt2-sqrt2=1-2sqrt2`
Đúng 2
Bình luận (0)






