Giả sử x = a/m ; y = b/m (a, b, m thuộc Z, m < 0) và x > y. Hãy chứng tỏ rằng nếu chọn z = (a + b) / 2m thì ta có x < z < y.
Sử dụng tính chất: Nếu a, b, c thuộc Z và a < b thì a + c < b + c
giả sử x=a/m , y = b/m
Giả sử x = a/m, y = b/m (a, b, m ∈ Z, b # 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = (a + b)/2m thì ta có x < z < y.
Tớ làm theo đề của cậu kia nhé.
Theo đề bài ta có:
\(x=\dfrac{a}{m},y=\dfrac{b}{m}\) (\(a, b, m\) \(\in\) Z, \(b\ne0\))
Vì \(x < y\) \(\Rightarrow\) \(a < b\)
Ta có:
\(x=\dfrac{2a}{2m}\)
\(y=\dfrac{2b}{2m}\)
\(z=\dfrac{\left(a+b\right)}{2m}\)
Vì \(a < b\)
\(\Rightarrow\) \(a + a < a + b\)
\(\Rightarrow\) \(2a < a + b\)
Do \(2a < a + b\) nên \(x < z\) \((1)\)
Vì \(a< b\)
\(\Rightarrow\) \(a + b < b + b\)
\(\Rightarrow\) \(a + b < 2b\)
Do \(a + b < 2b\) nên \(z < y\) \((2)\)
Từ \((1)\) và \((2)\) ta suy ra: \(x < z < y\)
Giả sử x=a/m y=b/m
Yêu cầu đề bài như thế nào vậy bạn?
giả sử X=a/m ,Y=b/m (a,b,m "thuộc"Z ,m>0) va x
Giả sử, x=a/m, y=b/m (với a,b, m thuộc Z, m>0) Chọn Z=a+b/2m.Chứng tỏ rằng nếu x<Z<y.
Giả sử x = a / m, y = b / m (a, b, m ∈ Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn Z = 2 a + 1 2 m thì ta có x < z < y.
Vì x < y nên 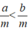 mà m > 0 nên a < b. Ta có
mà m > 0 nên a < b. Ta có
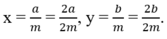
Chọn số 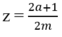 . Do 2a < 2a + 1 và m > 0 nên
. Do 2a < 2a + 1 và m > 0 nên 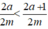 hay x < z. (1)
hay x < z. (1)
Do a < b và a; b ∈ Z nên a + 1 ≤ b suy ra 2a + 2 ≤ 2b.
Ta có 2a + 1 < 2a + 2 ≤ 2b nên 2a + 1 < 2b, do đó 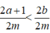 hay z < y. (2)
hay z < y. (2)
Từ (1) và (2) suy ra: x < z < y
Giả sử x= a/m, y= b/m(a,b,m thuộc Z,m>0) và x<y.CMR nếu chọn z=a+b/2m thì x<z<y
giả sử x=a/m ;y=b/m (a,b,c thuộc z, m>0). Chứng tỏ rằng z=a+b/2m
Giả sử: a,b >0 và m,n ∈ Z*
Tìm min của: \(P=ax^m+b\dfrac{1}{x^n}
\) với x>0
Lời giải:
Áp dụng BĐT Cô - si:
\(P=ax^m+\frac{b}{x^n}=\frac{a}{n}x^m+\frac{a}{n}x^m+...+\frac{a}{n}x^m+\frac{b}{mx^n}+...+\frac{b}{mx^n}\)
\(=(m+n)\sqrt[m+n]{(\frac{a}{n})^n.x^{mn}.(\frac{b}{m})^m.\frac{1}{x^{mn}}}\)
\(=(m+n)\sqrt[m+n]{\frac{a^nb^m}{n^n.m^m}}\)
giả sử x=a/m , y=b/m(a,b thuộc z , m>0) biết x<y , f=a+b/2m . chứng minh rằng :x<f<y
Giả sử x = \(\dfrac{a}{m}\); y = \(\dfrac{b}{m}\)(a;b;m ϵ Z, m ≠ 0 và x < y). Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì x < y < z.