ai giúp em câu hình với em cảm ơn :((
ai giúp em câu hình với em cảm ơn nhiều :((

ai giúp em câu hình với em cảm ơn ạ ;-;

ai giúp em câu hình với em cảm ơn ạ :((

Ai giúp em câu 6 với em cảm ơn ạ.

Có ai giúp em câu này với em cảm ơn.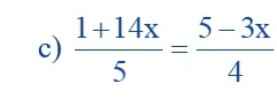
Lời giải:
$\frac{1+14x}{5}=\frac{5-3x}{4}$
$\Rightarrow 4(1+14x)=5(5-3x)$
$4+56x=25-15x$
$56x+15x=25-4$
$71x=21$
$x=\frac{21}{71}$
c, \(\Rightarrow4+56x=25-15x\Leftrightarrow71x=21\Leftrightarrow x=\dfrac{21}{71}\)

Có ai giúp em câu này với em cảm ơn.
số hs khá là: \(\dfrac{3}{4}\times\dfrac{1}{6}=\dfrac{1}{8}\left(hs\right)\)
a: số hs lớp 6A là : \(\dfrac{3}{4}+\dfrac{1}{8}+5=\dfrac{18}{24}+\dfrac{3}{24}+5=5\dfrac{21}{24}=5\dfrac{7}{8}=\dfrac{47}{8}\left(hs\right)\)
b: tỉ số là : \(\dfrac{3}{4}\times100:\dfrac{1}{8}=\dfrac{300}{4}:\dfrac{1}{8}=\dfrac{300\times8}{4\times1}=600\%\)
Gọi học sinh lớp 6a là x hs
Số học sinh giỏi là : \(\dfrac{3}{4}x\)(hs)
Số học sinh khác là : \(\dfrac{1}{6}.\dfrac{3}{4}x=\dfrac{1}{8}x\) (hs)
Theo bài ra có :
\(x-\dfrac{3}{4}x-\dfrac{1}{8}x=5\)
\(x\left(1-\dfrac{3}{4}-\dfrac{1}{8}\right)=5\)
\(\dfrac{1}{8}x=5\)
\(x=40\)
Vậy số hcj sinh lớp 6a là 40 hs
Số học sinh giỏi là : \(\dfrac{3}{4}.40=30\) (hs)
Số học sinh khá là :\(\dfrac{1}{6}.30=5\) (hs)
ĐS ...
Ai giúp em câu c với ạ em cảm ơn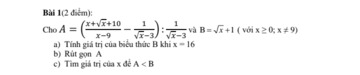
a: Thay x=16 vào B, ta được:
B=4+1=5
b: \(A=\dfrac{x+\sqrt{x}+10-\sqrt{x}-3}{x-9}\cdot\left(\sqrt{x}-3\right)=\dfrac{x+7}{\sqrt{x}+3}\)
c: Để A<B thì \(x+7< x+4\sqrt{x}+3\)
=>x>1
Ai giúp em câu này với em cảm ơn nhiều.
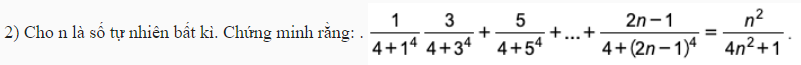
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
mọi người giải giúp em câu 71,74 với
em cảm ơn mọi người nhiều vẽ hình dùm em luôn em cảm ơn
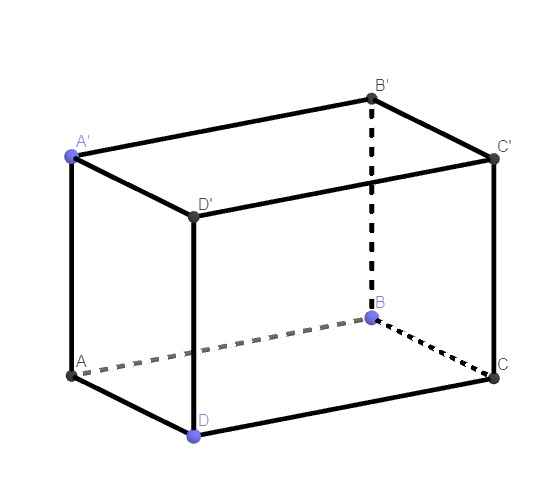
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)