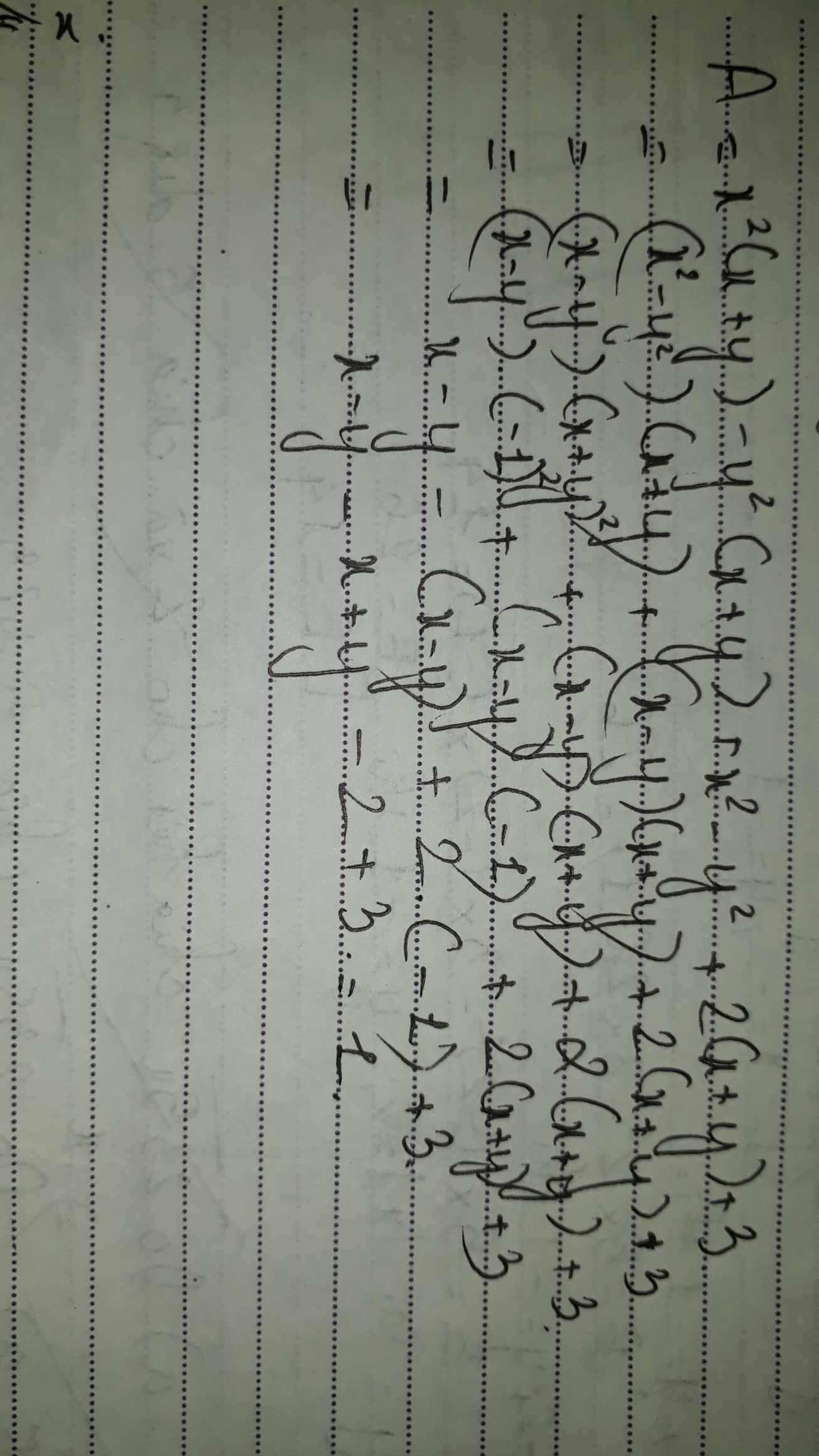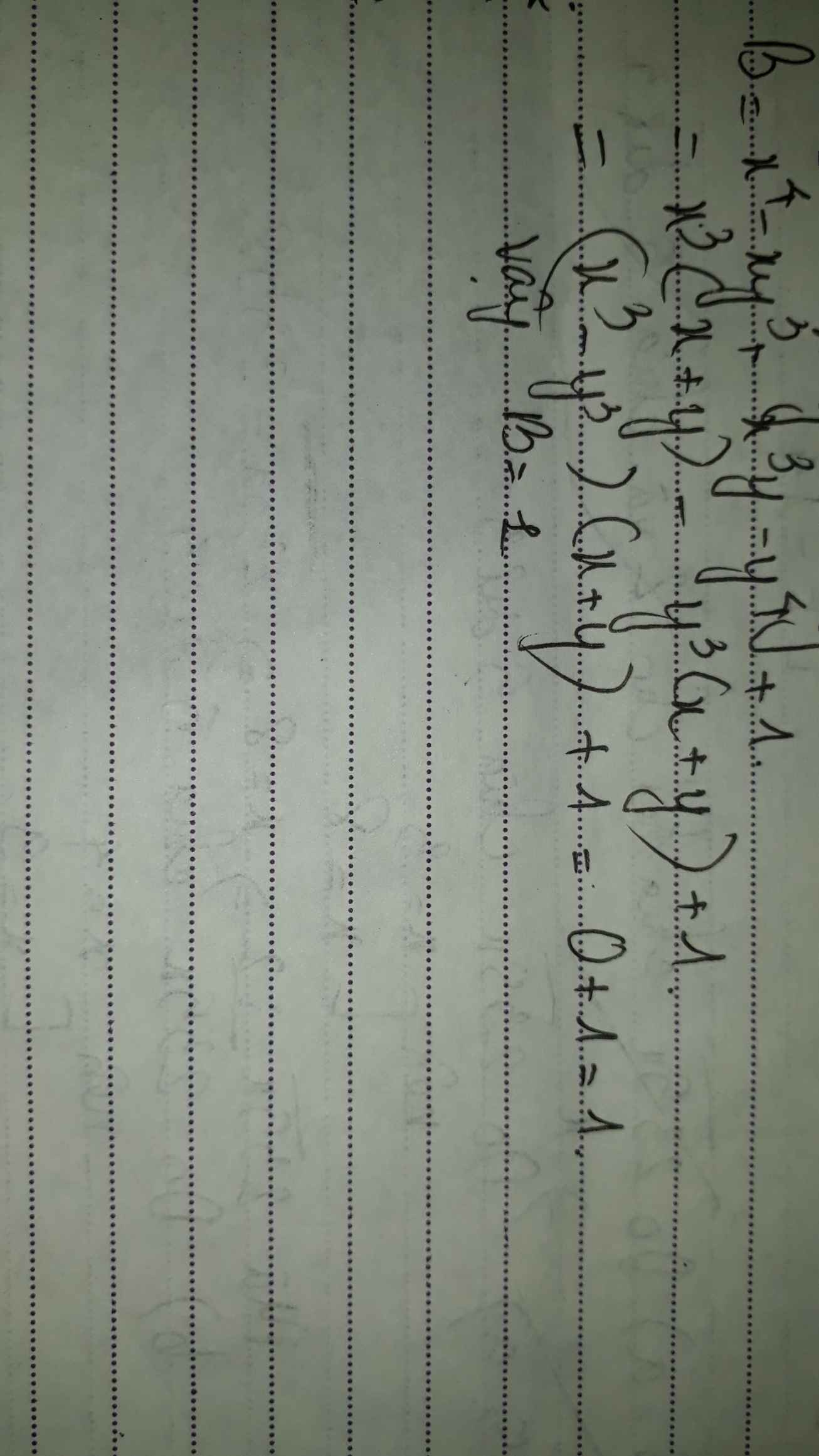cho x+y = 1.Tìm GTLN của Q=x3y+xy3
HN
Những câu hỏi liên quan
a) (x-y)(x4+x3y+x2y2+xy3+y4) = x5 - y5
b) (x + y)(x4 - x3y + x2y2 - xy3 + y4) = x5 + y5
c) (a +b)(a3 - a2b + ab2 - b3) = a4 - b4
d) (a + b)(a2 - ab + b2) = a3 + b3
a) (x-y)(x4+x3y+x2y2+xy3+y4) = x(x4+x3y+x2y2+xy3+y4)-y(x4+x3y+x2y2+xy3+y4) =(x5+x4y+x3y2+x2y2+xy4)-(x4y+x3y2+x2y2+xy4+y5) = x5+x4y+x3y2+x2y2+xy4-x4y-x3y2-x2y2-xy4-y5 =x5-y5⇒Điều cần chứng minh
Các câu b d tương tự
tính giá tri của các bieur thưc sau
a=x2(x+y)-y2(x+y)+x2-y2+2(x+y)+3 biết x+y+1=0
b=x4-xy3+x3y-y4+1 biết x+y=0
Chứng minh rằng: (x – y)(x4 + x3y + x2y2 + xy3 + y4) = x5 – y5
\(\left(x-y\right)\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)=x^5-y^5\)
Ta có VT:
\(\left(x-y\right)\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)\)
\(=x.x^4+x.x^3y+x.x^2y^2+x.xy^3+x.y^4-y.x^4-y.x^3y-y.x^2y^2-y.xy^3-y.y^4\)
\(=x^5+x^4y+x^3y^2+x^2y^3+xy^4-x^4y-x^3y^2-x^2y^3-xy^4-y^5\)
\(=x^5-y^5\)
VT=VP
Vậy:...
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi x, y ta luôn có:
(
x
4
-
x
3
y
+
x
2
y
2
-
xy
3
+
y
4
)
(
x
+
y...
Đọc tiếp
Chứng minh rằng với mọi x, y ta luôn có:
( x 4 - x 3 y + x 2 y 2 - xy 3 + y 4 ) ( x + y ) = x 5 + y 5 .
Thực hiện phép nhân đa thức với đa thức ở vế trái
=> VT = VP (đpcm)
Đúng 0
Bình luận (0)
Kết quả của phép chia
(
x
4
–
x
3
y
+
x
2
y
2
–
x
y
3
)
:
(
x
2
+
y
2...
Đọc tiếp
Kết quả của phép chia ( x 4 – x 3 y + x 2 y 2 – x y 3 ) : ( x 2 + y 2 ) là
A. (x – y)
B. x(x – y)
C. x 2 – y
D. x 2 + xy
Ta có
x 4 – x 3 y + x 2 y 2 – x y 3 = x 4 + x 2 y 2 – ( x 3 y + x y 3 ) = x 2 ( x 2 + y 2 ) – x y ( x 2 + y 2 ) = ( x 2 + y 2 ) ( x 2 – x y ) = ( x 2 + y 2 ) x ( x – y ) N ê n ( x 4 – x 3 y + x 2 y 2 – x y 3 ) : ( x 2 + y 2 ) = ( x 2 + y 2 ) x ( x – y ) : ( x 2 + y 2 ) = x ( x – y )
Đáp án cần chọn là : B
Đúng 0
Bình luận (0)
Đề: Thu gọn đơn thức sau đây và tìm bậc, hệ số của đơn thức
a) M = (- 2 x3y).(- 3 x2y3)
b) N = (- 3 x2y)2.(- 5 xy3)
a: M=(-2)*(-3)*x^3y*x^2y^3=6x^5y^4
Bậc là 9
Hệ số là 6
b: N=9x^4y^2*(-5)xy^3=-45x^5y^5
Bậc là 10
Hệ số là -45
Đúng 0
Bình luận (0)
BÀI TẬP PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG 1) xy3 – x3y 2) 15xy + 20x2 – 30x3)6x – 3xy4)x3 + 2x2 + x 5)4x3 – 12x2 + 9x 6)2x2y + 4xy2 – 10 x3y27)x4 + 2x3 + x2 11)x(x – 1) – y(1 – x)
Đọc tiếp
BÀI TẬP PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG
1) xy3 – x3y
2) 15xy + 20x2 – 30x
3)6x – 3xy
4)x3 + 2x2 + x
5)4x3 – 12x2 + 9x
6)2x2y + 4xy2 – 10 x3y2
7)x4 + 2x3 + x2
11)x(x – 1) – y(1 – x)
1, \(xy^3-x^3y=xy\left(y^2-x^2\right)=xy\left(y-x\right)\left(x+y\right)\)
2, \(5x\left(3y+4x-6\right)\)
3, \(3x\left(2-y\right)\)
4, \(x\left(x^2+2x+1\right)=x\left(x+1\right)^2\)
5, \(x\left(4x^2-12x+9\right)=x\left(2x-3\right)^2\)
6, \(2xy\left(x+2y-5x^2y\right)\)
7, \(x^2\left(x^2+2x+1\right)=x^2\left(x+1\right)^2\)
11, \(\left(x+y\right)\left(x-1\right)\)
Đúng 0
Bình luận (0)
\(1,xy^3-x^3y=xy\left(y^2-x^2\right)=xy\left(y-x\right)\left(y+x\right)\\ 2,15xy+20x^2-30x=5x\left(3y+4x-6\right)\\ 3,6x-3xy=3x\left(2-y\right)\\ 4,x^3+2x^2+x=x\left(x^2+2x+1\right)=x\left(x+1\right)^2\\ 5,4x^3-12x^2+9x=x\left(4x^2-12x+9\right)=x\left(2x-3\right)^2\\ 6,2x^2y+4xy^2-10x^3y^2=2xy\left(x+2y-5x^2y\right)\\ 11,x\left(x-1\right)-y\left(1-x\right)=x\left(x-1\right)+y\left(x-1\right)=\left(x-1\right)\left(x+y\right)\)
Đúng 0
Bình luận (0)
Cho biết công thức hóa học của hợp chất của nguyên tố X với O và hợp chất của nguyên tố Y với H như sau (X, Y là những nguyên tố nào đó): XO, YH3. Hãy chọn công thức hóa học nào là đúng cho hợp chất của X với Y trong số các công thức sau đây: A. XY3. B. X3Y. C. X2Y3. D. X3Y2. E. XY.
Đọc tiếp
Cho biết công thức hóa học của hợp chất của nguyên tố X với O và hợp chất của nguyên tố Y với H như sau (X, Y là những nguyên tố nào đó): XO, YH3.
Hãy chọn công thức hóa học nào là đúng cho hợp chất của X với Y trong số các công thức sau đây:
A. XY3.
B. X3Y.
C. X2Y3.
D. X3Y2.
E. XY.
* Gọi hóa trị của X trong công thức 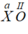 là a
là a
Theo quy tắc hóa trị ta có : a.1 = II.1 ⇒ a = II
⇒ X có hóa trị II
* Gọi hóa trị của Y trong công thức 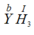 là b
là b
Theo quy tắc hóa trị ta có : b.1 = I.3 ⇒ b = 3
⇒ Y có hóa trị III
* Hợp chất X(II) và Y(III) có công thức dạng chung là 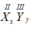
Theo quy tắc hóa trị ta có : II.x = III.y ⇒ 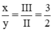 ⇒ x = 3, y = 2
⇒ x = 3, y = 2
⇒ Công thức là X3Y2. Đáp án D
Đúng 1
Bình luận (1)
Bài 10: Chứng minh rằng nếu a = x3y; b = x2y2; c = xy3 thì với bất kì số hữu tỉ x và y nào ta cũng có: ax + b2 – 2x4y4 = 0 ?
Công thức hóa học của hợp chất tạo bởi nguyên tố X với nhóm SO4 là X2(SO4)3 và hợp chất tạo bởi nhóm nguyên tử Y với H là HY. Công thức hoá học của hợp chất giữa nguyên tố X với nhóm nguyên tử Y là
A. XY2 B. X3Y C. XY3 D. XY
Có: \(X_2\left(SO_4\right)_3\)
Áp dụng công thức Hoá trị ta được:
\(x.2=II.3\) => \(x=\dfrac{II.3}{2}=\dfrac{2.3}{2}=\dfrac{6}{2}=3\)
=> X hoá trị III
Tương tự: \(HY\)
Áp dụng công thức Hoá trị ta được:
\(x.1=I.1\) => \(x=\dfrac{I.1}{1}=\dfrac{1}{1}=1\)
=> Y hoá trị I
Vậy: Công thức hoá học của hợp chất đó là: \(XY_3\). Chọn \(C\)
Đúng 2
Bình luận (0)