vẽ hình ra luôn ạ!
giải chi tiết ra giúp mình luôn ạ, vẽ hình luôn, hôm nay mik phải nọp rùi, mình cảm ơn mn rât nhiều

1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)
Mn giúp e với ạ
Cho hình thoi abcd có độ dài hai đường chéo là 14cm và 22cm. Tính độ dài cạnh của hình thoi
Mn vẽ hình ra luôn giúp e, e cảm ơn ạ
Hình bạn vẽ hai đường chéo và chúng cắt nhau tại trung điểm của mỗi đường và vuông góc nhé.
Ta có: ABCD là hình thoi => \(AC\perp BD\)
\(AC\cap BD=\left\{O\right\}\)
Xét △AOB có:
\(AB^2=AO^2+OB^2\left(Pytago\right)\)
\(\Rightarrow AB^2=7^2+11^2\)
\(\Rightarrow AB=\sqrt{7^2+11^2}\approx13\left(cm\right)\)
Giúp e câu 9 10 đi ạ scan vẽ hình thì vẽ luôn ạ
Câu 9.
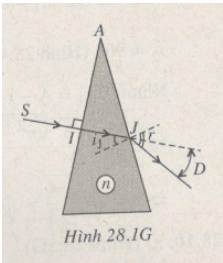
Tại điểm \(I\): \(i=r=0\)
Tia sáng truyền thẳng vào lăng kính.
Tại điểm J có \(i_J=30^o\)
Theo định luật khúc xạ ánh sáng:
\(sinr=nsini_J=1,5\cdot sin30^o=\dfrac{3}{4}\Rightarrow r=arcsin\dfrac{3}{4}\)
Góc lệch:
\(D=r-i_J=arcsin\dfrac{3}{4}-30^o\approx18,6^o\)
Chọn B.
Hình vẽ tham khảo sgk lí 11!!!
Vẽ hình luôn ạ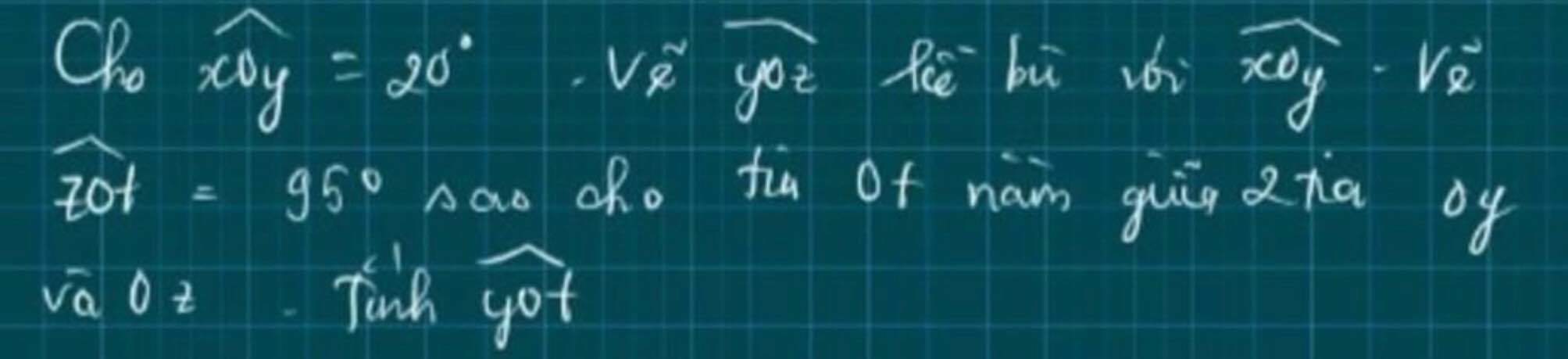
 vẽ hình luôn ạ
vẽ hình luôn ạ
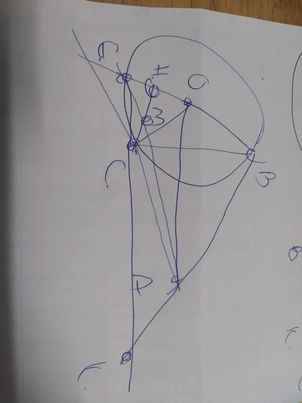
1: Ta có: ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
Xét tứ giác OCAD có
I là trung điểm chung của OA và CD
=>OCAD là hình bình hành
Hình bình hành OCAD có OC=OD
nên OCAD là hình thoi
2: Ta có: OCAD là hình thoi
=>OA là phân giác của góc COD
Xét ΔOCM và ΔODM có
OC=OD
\(\widehat{COM}=\widehat{DOM}\)
OM chung
Do đó: ΔOCM=ΔODM
=>\(\widehat{OCM}=\widehat{ODM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{ODM}=90^0\)
=>MD là tiếp tuyến của (O)
3:
Xét (O) có
ΔCFE nội tiếp
CE là đường kính
Do đó: ΔCFE vuông tại F
=>CF\(\perp\)FE tại F
=>CF\(\perp\)ME tại F
Xét ΔCME vuông tại C có CF là đường cao
nên \(MF\cdot ME=MC^2\left(1\right)\)
Xét ΔMCO vuông tại C có CI là đường cao
nên \(MI\cdot MO=MC^2\left(2\right)\)
Từ (1) và (2) suy ra \(MF\cdot ME=MI\cdot MO\)
=>\(\dfrac{MF}{MO}=\dfrac{MI}{ME}\)
Xét ΔMFI và ΔMOE có
\(\dfrac{MF}{MO}=\dfrac{MI}{ME}\)
\(\widehat{FMI}\) chung
Do đó: ΔMFI đồng dạng với ΔMOE
Vẽ hình luôn với ạ

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
Vẽ hình luôn giúp em ạ
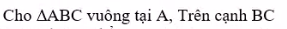

a: Xét ΔCAD vuông tại A và ΔCED vuông tại E có
CD chung
CA=CE
Do đó:ΔCAD=ΔCED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDB vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDB}\)
Do đó:ΔADK=ΔEDB
c: AB=8cm

 vẽ hình luôn giúp em ạ
vẽ hình luôn giúp em ạ
3:
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔDCB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3*8=16/3cm
c: Gọi H là trung điểm của AC
=>HQ//AD(HQ vuông góc AC)
mà H là trung điểm của AC
nên Q là trung điểm của CD
=>B,M,Q thẳng hàng

vẽ hình luôn ạ cảm ơn
1:
a: Xét ΔOBA và ΔOCA có
OB=OC
AB=AC
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
mà \(\widehat{OBA}=90^0\)
nên \(\widehat{OCA}=90^0\)
=>AC\(\perp\)OC tại C
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBCE nội tiếp
BE là đường kính
Do đó: ΔBCE vuông tại C
=>BC\(\perp\)CE tại C
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Ta có: OA\(\perp\)BC
CE\(\perp\)CB
Do đó: OA//CE
2: Gọi giao điểm của EC với BA là K
Ta có: BC\(\perp\)CE tại C
=>BC\(\perp\)EK tại C
=>ΔBCK vuông tại C
Ta có: \(\widehat{ACK}+\widehat{ACB}=\widehat{BCK}=90^0\)
\(\widehat{AKC}+\widehat{ABC}=90^0\)(ΔBCK vuông tại C)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ACK}=\widehat{AKC}\)
=>AC=AK
mà AC=AB
nên AK=AB(3)
Ta có: CH\(\perp\)BE
BA\(\perp\)BE
Do đó: CH//BA
Xét ΔEBA có MH//BA
nên \(\dfrac{MH}{BA}=\dfrac{EM}{EA}\left(4\right)\)
Xét ΔEAK có MC//AK
nên \(\dfrac{MC}{AK}=\dfrac{EM}{EA}\left(5\right)\)
Từ (3),(4),(5) suy ra MH=MC
=>M là trung điểm của CH