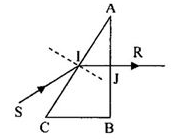
Vẽ hình luôn giúp em ạ
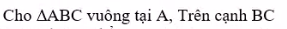

mọi người giúp em với ạ, vẽ luôn hình ạ, em cảm ơn.

 vẽ hình luôn giúp em ạ
vẽ hình luôn giúp em ạ
3:
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔDCB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3*8=16/3cm
c: Gọi H là trung điểm của AC
=>HQ//AD(HQ vuông góc AC)
mà H là trung điểm của AC
nên Q là trung điểm của CD
=>B,M,Q thẳng hàng
làm giúp em 2 bài này đc ko ạ( vẽ hình luôn ạ). EM CẢM ƠN![]()

Bài 9:
a: Xét tứ giác OPMN có
góc OPM+góc ONM=180 độ
=>OPMN là tứ giác nội tiếp
b: \(MN=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH vuông góc AB
Xét tứ giác OHNM có
góc OHM=goc ONM=90 độ
=>OHNM là tứ giác nội tiép
=>góc MHN=góc MON
cho tia ox vẽ 2 tia oy và oz sao cho góc xoy = 110 độ , xoz = 150 độ .
tính yoz .![]() vẽ hình luôn ạ !
vẽ hình luôn ạ !
giúp em với mai em phải nộp rồi ạ
góc xOy<góc xOz
=>Oy nằm giữa Ox và Oz
=>góc xOy+góc yOz=góc xOz
=>góc yOz=40 độ
Giúp e câu 9 10 đi ạ scan vẽ hình thì vẽ luôn ạ
Câu 9.
Tại điểm \(I\): \(i=r=0\)
Tia sáng truyền thẳng vào lăng kính.
Tại điểm J có \(i_J=30^o\)
Theo định luật khúc xạ ánh sáng:
\(sinr=nsini_J=1,5\cdot sin30^o=\dfrac{3}{4}\Rightarrow r=arcsin\dfrac{3}{4}\)
Góc lệch:
\(D=r-i_J=arcsin\dfrac{3}{4}-30^o\approx18,6^o\)
Chọn B.
Hình vẽ tham khảo sgk lí 11!!!
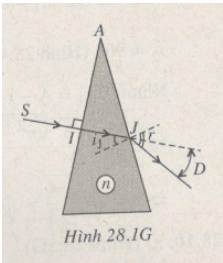
Mọi người giúp em làm bài toán hình này với ạ, kèm vẽ hình luôn nhé ạ. Em cảm ơn nhiều. - Cho hình chữ nhật ABCD có AB=8cm, BC= 6cm. Vẽ đường cao AH của tam giác ABD. a) chứng minh tam giác HBA đồng dạng với tam giác CDB b) Chứng minh: AD^2 = DH. DB c) Tính độ dài đoạn thẳng DH và AH
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
( sử dụng thước vẽ lại cho chính xác nhé. )
a. xét tam giác HBA và tam giác CDB, ta có :
góc B là góc chung ( gt )
góc H = góc D = 90 độ
do đó : tam giác HBA đồng dạng tam giác CDB ( g - g )
b.
• AD/DB = DH/BC
mà BC = AD ( vì ABCD là hcn )
nên AD/BD = DH/AD
= AD . AD = DB . DH
=> AD^2 = DB . DH ( đpcm )
• vì AB = DC ( ABCD là hcn )
nên DC = 8 cm
áp dụng định lý pytago trong tam giác DBC vuông tại C, ta có:
DB^2 = BC^2 + CD^2
DB^2 = 8^2 + 6^2
DB^2 = 64 + 36
DB^2 = 100
DB = căn bậc 2 của 100
DB = 10 ( cm )
vậy DB = 10 cm
Vẽ hình hộ em luôn với ạ

\(M\in SA\subset\left(SAB\right)\)
\(M\in\left(P\right)\)
Do đó: \(M\in\left(SAB\right)\cap\left(P\right)\)
Xét (SAB) và (P) có
\(M\in\left(SAB\right)\cap\left(P\right)\)
AB//CD
Do đó: \(\left(SAB\right)\cap\left(P\right)=xy\), xy đi qua M và xy//AB//CD
Vẽ hình r làm luôn giúp mình ạ
Giúp e câu 11 vẽ hình luôn ạ
Theo đinh luật khúc xạ ánh sáng (tại điểm \(I\)) :
\(sini_1=nsinr_1\)
\(\Rightarrow sin45^o=\sqrt{2}\cdot sinr_1\Rightarrow sinr_1=\dfrac{1}{2}\Rightarrow r_1=30^o\)
Tam giác ABC đều\(\Rightarrow\)Góc chiết quang \(\widehat{A}=60^o=r_1+r_2\)
\(\Rightarrow r_2=30^o\)
Xét tại điểm J, theo định luật khúc xạ ánh sáng:
\(sini_2=nsinr_2=\sqrt{2}\cdot sin30^o=\dfrac{\sqrt{2}}{2}\Rightarrow i_2=45^o\)
Góc lệch tia ló ra khỏi lăng kính so với tia tới:
\(D=i_1+i_2-A=45^o+45^o-60^o=30^o\)
Chọn A