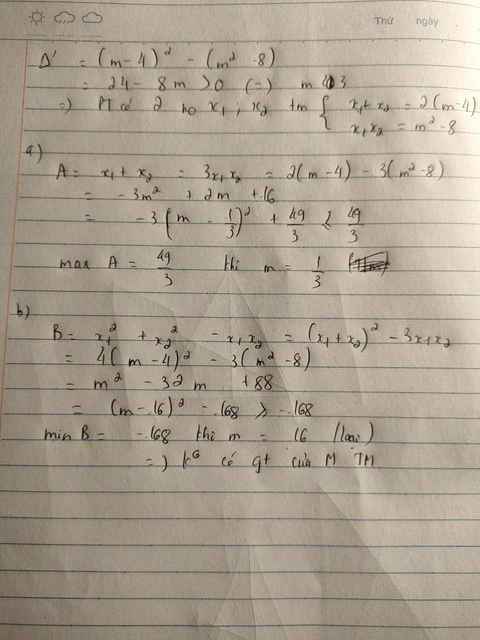\(A=\frac{32}{2+x_1^2}\cdot\frac{x_1+x_2+x_1x_2}{2+x^2_2}\)
NL
Những câu hỏi liên quan
giả sử \(x_1,x_2\) là nghiệm của phương trình \(x^2-2\sqrt{5}x+2\)=0 Tính giá trị biểu thức E=\(\dfrac{x_1^2+x_1x_2+x^2_2}{x_1^2+x^2_2}\)
\(\Delta'=\left(-\sqrt{5}\right)^2-1.2=5-2=3>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2\sqrt{5}\\x_1x_2=2\end{matrix}\right.\)
\(E=\dfrac{x^2_1+x_1x_2+x^2_2}{x^2_1+x^2_2}\\
=\dfrac{\left(x_1+x_2\right)^2-x_1x_2}{\left(x_1+x_2\right)^2-2x_1x_2}\\
=\dfrac{\left(2\sqrt{5}\right)^2-2}{\left(2\sqrt{5}\right)^2-2.2}\\
=\dfrac{20-2}{20-4}\\
=\dfrac{18}{16}\\
=\dfrac{9}{8}\)
Đúng 2
Bình luận (0)
\(E=\dfrac{\left(x_1+x_2\right)^2-x_1x_2}{\left(x_1+x_2\right)^2-2x_1x_2}=\dfrac{4.5-2}{4.5-2.2}=\dfrac{18}{16}=\dfrac{9}{8}\)
Đúng 2
Bình luận (1)
Cho phương trình \(x^2-2\left(m+4\right)x+m^2-8=0\)
Tìm m để phương trình thỏa mãn \(x_1,x_2\) thỏa mãn:
\(A=x^2_1+x^2_2-x_1-x_2\) đạt giá trị nhỏ nhất.
\(B=x^2_1+x^2_2-x_1x_2\) đạt giá trị nhỏ nhất.
\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16
Đúng 3
Bình luận (0)
Cho pt: \(2x^2+2mx+m^2-2=0\). Gọi \(x_1,x_2\) là 2 nghiệm của pt.Tìm GTNN và GTLN của biểu thức A=\(\frac{2x_1x_2+3}{x_1^2+x^2_2+2\left(x_1x_2+1\right)}\)
\(\Delta'=m^2-2\left(m^2-2\right)=4-m^2\ge0\Rightarrow-2\le m\le2\)
Khi đó ta có \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=\frac{m^2-2}{2}\end{matrix}\right.\)
\(A=\frac{2x_1x_2+3}{x_1^2+x_2^2+2x_1x_2+2}=\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=\frac{m^2+1}{m^2+2}=1-\frac{1}{m^2+2}\)
Do \(0\le m^2\le4\Rightarrow\frac{1}{6}\le\frac{1}{m^2+2}\le\frac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}A_{min}=1-\frac{1}{2}=\frac{1}{2}\Rightarrow m=0\\A_{max}=1-\frac{1}{6}=\frac{5}{6}\Rightarrow m=\pm2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\text{f(x) = }ax^2+bx+c,a\ne0\text{ có 2 nghiệm phân biệt }x_1,x_2\text{ thì x_1+x_2=}-\frac{b}{a},x_1x_2=\frac{c}{a}\)
1 . Cho pt :x^2-mx+m-10 . Tìm m để pt có 2 nghiệm x_1,x_2 và biểu thức Adfrac{2x_1x_2+3}{x^2_1+x^2_2+2left(x_1x_2+1right)} đạt GTLN2.Giả sử m là giá trị để phương trình x^2-mx+m-20 có 2 nghiệm x_1,x_2 thỏa mãn dfrac{x_1^{^2}-2}{x_1-1}.dfrac{x^2_2-2}{x_2-1}4 . Tìm các giá trị của m
Đọc tiếp
1 . Cho pt :\(x^2-mx+m-1=0\) . Tìm m để pt có 2 nghiệm \(x_1,x_2\) và biểu thức \(A=\dfrac{2x_1x_2+3}{x^2_1+x^2_2+2\left(x_1x_2+1\right)}\) đạt GTLN
2.Giả sử m là giá trị để phương trình \(x^2-mx+m-2=0\) có 2 nghiệm \(x_1,x_2\) thỏa mãn \(\dfrac{x_1^{^2}-2}{x_1-1}.\dfrac{x^2_2-2}{x_2-1}=4\) . Tìm các giá trị của m
1.
\(a+b+c=0\) nên pt luôn có 2 nghiệm
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(A=\dfrac{2x_1x_2+3}{x_1^2+x_2^2+2x_1x_2+2}=\dfrac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=\dfrac{2\left(m-1\right)+3}{m^2+2}=\dfrac{2m+1}{m^2+2}\)
\(A=\dfrac{m^2+2-\left(m^2-2m+1\right)}{m^2+2}=1-\dfrac{\left(m-1\right)^2}{m^2+2}\le1\)
Dấu "=" xảy ra khi \(m=1\)
2.
\(\Delta=m^2-4\left(m-2\right)=\left(m-2\right)^2+4>0;\forall m\) nên pt luôn có 2 nghiệm pb
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-2\end{matrix}\right.\)
\(\dfrac{\left(x_1^2-2\right)\left(x_2^2-2\right)}{\left(x_1-1\right)\left(x_2-1\right)}=4\Rightarrow\dfrac{\left(x_1x_2\right)^2-2\left(x_1^2+x_2^2\right)+4}{x_1x_2-\left(x_1+x_2\right)+1}=4\)
\(\Rightarrow\dfrac{\left(x_1x_2\right)^2-2\left(x_1+x_2\right)^2+4x_1x_2+4}{x_1x_2-\left(x_1+x_2\right)+1}=4\)
\(\Rightarrow\dfrac{\left(m-2\right)^2-2m^2+4\left(m-2\right)+4}{m-2-m+1}=4\)
\(\Rightarrow-m^2=-4\Rightarrow m=\pm2\)
Đúng 1
Bình luận (2)
\(x^2_1+x^2_2+x_1x_2\left(x_1+x_2\right)\)
Theo hệ thức Vi-et : \(x_1+x_2=\dfrac{-b}{a}\) và \(x_1x_2=\dfrac{c}{a}\)
\(x_1^2+x_2^2+x_1x_2\left(x_1+x_2\right)\)
=\(\left(x_1+x_2\right)^2-2x_1x_2+x_1x_2\left(x_1+x_2\right)\)
=\(\left(\dfrac{-b}{a}\right)^2-2\dfrac{c}{a}+\dfrac{c}{a}\left(\dfrac{-b}{a}\right)\)
=\(\dfrac{b^2}{a^2}-\dfrac{2c}{a}+\dfrac{-bc}{a^2}\)
=\(\dfrac{b^2-2ac-bc}{a^2}\)
Đúng 1
Bình luận (0)
Cho PT \(x^2+2\left(m-2\right)x+m^2-2m+4=0\). Tìm m để PT có 2 nghiệm thực phân biệt \(x_1,x_2\)Thỏa mãn \(\frac{2}{x^2_1+x^2_2}-\frac{1}{x_1x_2}=\frac{1}{15m}\)
Ta có để pt có 2 nghiệm phân biệt thì:
\(\Delta'=\left(m-2\right)^2-\left(m^2-2m\right)>0\)
\(\Leftrightarrow m< 2\)
Theo vi-et ta có
\(\hept{\begin{cases}x_1+x_2=4-2m\\x_1x_2=m^2-2m\end{cases}}\)
Theo đề ta có: \(\frac{2}{x_1^2+x_2^2}-\frac{1}{x_1x_2}=\frac{1}{15m}\)
\(\Leftrightarrow\frac{2}{\left(x_1+x_2\right)^2-4x_1x_2}-\frac{1}{x_1x_2}=\frac{1}{5m}\)
\(\Leftrightarrow\frac{2}{\left(4-2m\right)^2-4\left(m^2-2m\right)}-\frac{1}{m^2-2m}=\frac{1}{15m}\)
\(\Leftrightarrow\frac{1}{8-4m}-\frac{1}{m^2-2m}=\frac{1}{15m}\)
\(\Leftrightarrow19m+52=0\)
\(\Leftrightarrow m=\frac{52}{19}\)(loại)
Không có m thỏa cái trên
PS: Không biết có nhầm chỗ nào không. Bạn kiểm tra hộ m nhé
Đúng 0
Bình luận (0)
Cho phương trình \(x^2-2\left(m+1\right)x+m^2+\)3=0
Định m để phương trình có 2 nghiệm x1, x2 thỏa \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{8}{x_1x_2}\)
\(\Delta=\left[-2\left(m+1\right)\right]^2-4\left(m^2+3\right)\)
= 4(m + 1)2 - 4m2 - 12
= 4m2 + 8m + 4 - 4m2 - 12 = 8m - 8
Để pt có 2 nghiệm thì \(\Delta\ge0\) <=> 8m - 8 \(\ge\)0
<=> 8(m - 1) \(\ge\) 0
<=> m -1 \(\ge\)0
<=> m \(\ge\) 1
Theo vi-et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)=2m+2\\x_1.x_2=m^2+3\end{cases}}\)
Theo đề ta có: \(\frac{x1}{x2}+\frac{x2}{x1}=\frac{8}{x1.x2}\)
ĐK: x1, x2 \(\ne\)0 => \(\hept{\begin{cases}x1+x2\ne0\\x1.x2\ne0\end{cases}}hay\hept{\begin{cases}2m+2\ne0\\m^2+3\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}m\ne-1\\m^2\ne-3\end{cases}}\Leftrightarrow m\ne-1\)
<=> \(\frac{\left(x_1\right)^2+\left(x_2\right)^2}{x1.x2}=\frac{8}{x1.x2}\)
=> \(\left(x_1\right)^2+\left(x_2\right)^2=8\)
<=> \(\left(x_1+x_2\right)^2-2.x_1.x_2=8\)
Hay (2m + 2)2 - 2(m2 + 3) = 8
<=> 4m2 + 8m + 4 - 2m2 - 6 = 8
<=> 2m2 + 8m - 10 = 0
a + b + c = 2 + 8 + (-10) = 0
=> m = 1 (tmđk) và m = \(\frac{c}{a}=-5\)(ktmđk)
Vậy m = 1 thì ....
Tìm m để pt để bt A= \(\frac{2x_1x_2+3}{x_1^2+x^2_2+2\left(x_1x_2+1\right)}\)dat GTNN
Áp dụng Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}\Rightarrow A=\frac{2m+1}{m^2+2}\left(1\right)}\)Tìm đk để pt (1) có nghiệm theo ẩn
\(\Rightarrow\frac{-1}{2}\le P\)
Dấu "=" xảy ra <=> m=-2