Tìm min: 1+cosa+1/cosa
BP
Những câu hỏi liên quan
Tìm min của \(\frac{1+sina}{cosa}\)+ \(\frac{1+cosa}{sina}\)
Giúp em bài này với ạ
a) \(\frac{1-sina}{cosa}=\frac{cosa}{1+sina}\)
b) \(\frac{sina}{1+cosa}+\frac{1+cosa}{sina}=\frac{2}{sina}\)
c) \(\frac{cosa}{1+sina}+\frac{cosa}{1-sina}=\frac{2}{cosa}\)
Giả sử các biểu thức đều xác định
a/ \(\frac{1-sina}{cosa}=\frac{cosa\left(1-sina\right)}{cos^2a}=\frac{cosa\left(1-sina\right)}{1-sin^2a}=\frac{cosa\left(1-sina\right)}{\left(1-sina\right)\left(1+sina\right)}=\frac{cosa}{1+sina}\)
b/ \(=\frac{sin^2a+\left(1+cosa\right)^2}{sina\left(1+cosa\right)}=\frac{sin^2a+cos^2a+2cosa+1}{sina\left(1+cosa\right)}=\frac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\frac{2}{sina}\)
c/ \(=\frac{cosa\left(1-sina\right)+cosa\left(1+sina\right)}{\left(1-sina\right)\left(1+sina\right)}=\frac{2cosa}{1-sin^2a}=\frac{2cosa}{cos^2a}=\frac{2}{cosa}\)
Chứng minh các hằng đẳng thức trên
Sina/sina- cosa - cosa/cosa - Sina = 1+cot²a /1- cot²a
Tìm a ∈ (0; 2 π ) để hàm số sau đồng biến trên khoảng (1; + ∞ ).
y = 1 3 x 3 - 1 2 (1 + cosa) x 2 + 2x cosa + 1
Tập xác định: D = R; y′ = x 2 − (1 + 2cosa)x + 2cosa
y′= 0 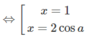
Vì y’ < 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa ≤ 1
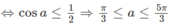
(vì a ∈ (0; 2 π ).
Đúng 0
Bình luận (0)
Chứng minh đẳng thức sau:Sina/Sina - cosa - cosa/cosa- Sina = 1+ cot²a/1-cot²a
Xem chi tiết
\(\dfrac{sina}{sina-cosa}-\dfrac{cosa}{cosa-sina}=\dfrac{sina+cosa}{sina-cosa}=\dfrac{1+cota}{1-cota}=\dfrac{\left(1+cota\right)^2}{1-cot^2a}\)
Đề bài ko đúng
Đúng 0
Bình luận (0)
Sin²a/Sina - cosa - Sina + cosa / tan²a -1 = Sina+ cosa
Cho tana=\(\dfrac{1}{3}\)Tính\(\dfrac{cosa-sina}{cosa+sina}\)
Chứng minh rằng:\(\dfrac{1-tana}{1+tana}=\dfrac{cosa-sina}{cosa+sina}\)
Rút gọn: \(\dfrac{sina+cosa-1}{sina-cosa+1}\)
\(b)\frac{(sina+cosa)^2-(sina-cosa)^2}{sina.cosa}=4\)
chứng minh các hệ thức sau
\(a) \frac{cosa}{1-sina}=\frac{1+sina}{cosa}\)
b) khai triển hằng đẳng thức là ra
a) nhân tích chéo
Đúng 0
Bình luận (0)
\(\frac{\cos\alpha}{1-\sin\alpha}=\frac{1+\sin\alpha}{\cos\alpha}\Leftrightarrow\cos^2\alpha=1-\sin^2\alpha\)\(\Leftrightarrow\cos^2\alpha+\sin^2\alpha=1\)(luôn đúng)
\(\frac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha\cdot\cos\alpha}=\frac{\sin^2\alpha+\cos^2\alpha+2\sin\alpha\cdot\cos\alpha-\sin^2\alpha-\cos^2\alpha+2\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}\)
\(=\frac{4\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}=4\)(đpcm)
Đúng 0
Bình luận (0)

