1. Cho ABC vuông cân tại A, cạnh huyền BC = 2cm. Tính các cạnh góc vuông.
NS
Những câu hỏi liên quan
Cho 1 tam giác vuông cân ABC ( vuông cân tại A).Tính cạnh huyền BC biết cạnh góc vuông dài 5 cm
bc^2= ac^2+ab^2 ( định lí pytago)
bc^2=5^2+5^2
=25+25
=50
bc= căn 50
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm
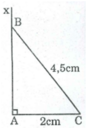
Cách dựng:
- Dựng đoạn AC = 2cm.
- Dựng góc ∠ (CAx) bằng 90 0
- Dựng cung tròn tâm C bán kính 4,5cm cắt Ax tại B. Nối CB ta có ΔABC cần dựng .
Chứng minh:
∆ ABC có ∠ A = 90 0 , AC = 2 cm, BC = 4,5 cm.
Thỏa mãn điều kiện bài toán.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
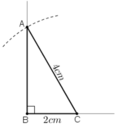
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
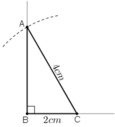
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4,5cm và cạnh góc vuông AC = 2cm ?
Cho tam giác ABC vuông cân tại A , BC = 2cm . Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E
Tính các góc và các cạnh của hình thang AECB
Bài 2: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB AC 2dmA. BC 4 dm B. BC √6 dm C. BC 8dm D. BC √8 dmBài 3: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?A. 10 cm, 22 cm B. 10 cm, 24 cm C. 12 cm, 24 cm D. 15 cm, 24 cmBài 4: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:A. 15 cm; 8 cm; 18 cmB. 21 cm; 20 cm; 29 cmC. 5 cm; 6 cm; 8 cmD. 2 cm; 3 cm; 4 cmBài 5: Cho tam g...
Đọc tiếp
Bài 2: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB = AC = 2dm
A. BC = 4 dm B. BC = √6 dm C. BC = 8dm D. BC = √8 dm
Bài 3: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?
A. 10 cm, 22 cm B. 10 cm, 24 cm C. 12 cm, 24 cm D. 15 cm, 24 cm
Bài 4: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
A. 15 cm; 8 cm; 18 cm
B. 21 cm; 20 cm; 29 cm
C. 5 cm; 6 cm; 8 cm
D. 2 cm; 3 cm; 4 cm
Bài 5: Cho tam giác ABC vuông tại A. Kẻ AD ⊥ BC tại D. Biết AB = 7 cm, BD = 4 cm. Khi đó AD có độ dài là:
A. AD = 33 cm
B. AD = 3 cm
C. AD = √33 cm
D. AD = √3 cm
Bài 2: D
Bài 3: B
Bài 4: B
bài 5: C
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4m, cạnh góc vuông BC = 2cm
Bài giải:
Sử dụng phương pháp dựng phương pháp vuông đã được học.
Ta lần lượt thực hiện:
- Vẽ góc vuông xBy. Trên tia Bx lấy điểm C sao cho BC = 2cm.
- Vẽ đường tròn (C; 4) và đường tròn này cắt tia Oy tại A.
Nối A với C ta được ∆ABC là tam giác cần dựng.
Đúng 0
Bình luận (0)
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
giả sử ta đã có tam giác ABC vuông tại B
áp dụng định lí py-ta-go vào tam giác ABC vuông tại B có:
BC2+AB2=AC2
22+AB2=42
4+AB2=16
AB2=12
=>AB=\(\sqrt{12}\)(cm)
Các bước vẽ :
B1: vẽ đoạn thẳng AC = 4cm
B2: dùng com-pa vẽ một đường tròn tâm A bán kính 2 cm
B3: dùng com-pa vẽ một đường tròn tâm AB bán kính \(\sqrt{12}cm\)
B4 : 2 đường tròn cắt nhau tại một điểm điểm đó là B nói 3 điểm A;B;C lại với nhau ta được tam giác ABC vuông tại B có cạnh huyền AC=4cm cạnh góc vuông BC=2cm
Đúng 0
Bình luận (0)
bài này cần 4 bước:
- Phân tích
- dựng hình
- chứng minh
-biện luận
Đúng 0
Bình luận (0)
1) phân tích:
Giả sử dựng được tam giác ABC thỏa mãn yêu cầu. Ta thấy:
- Cạnh BC dựng được ngay khi biết BC = 2 cm
- Dựng góc vuông xBC = 90o
- Cạnh CA biết 2 yếu tố: CA = 4 cm và A thuộc đường thẳng Bx
2) cách dựng:
- Dựng đoạn BC = 2 cm
- Dựng đường thẳng Bx vuông góc với BC
- Dựng đường tròn (C; 4 cm) cắt Bx tại A
- Nối A với C ta được tam giác ABC cần dựng
3) chứng minh:
Bx vuông góc với BC ; A thuộc Bx nên tam giác ABC vuông tại B
Tam giác ABC thỏa mãn: BC = 2; CA = 4 cm
4) Bài toán chỉ có 1 nghiệm hình
Đúng 0
Bình luận (0)




