Tìm tất cả các đa thức thỏa: x4 + 2x3 +3x2 + 2x + 1 = P2(x)
Help me!!!
Cho p ( x ) = 5 x 4 + 4 x 3 - 3 x 2 + 2 x - 1 và q ( x ) = - x 4 + 2 x 3 - 3 x 2 + 4 x - 5
Tính p(x) + q(x) rồi tìm bậc của đa thức thu được
A. p ( x ) + q ( x ) = 6 x 3 - 6 x 2 + 6 x - 6 có bậc là 6
B p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x + 6 có bậc là 4
C. p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 có bậc là 4
D. P ( x ) + q ( x ) = 4 x 4 + 6 x 3 + 6 x - 6 c ó b ậ c l à 4
Ta có p(x) + q(x)
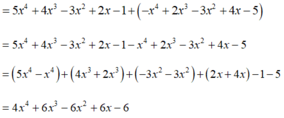
Bậc của đa thức p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 l à 4
Chọn đáp án C
Phân tích các đa thức sau thành nhân tử
a,x4+2x3+3x2+2x+1
b,x4-4x3+2x2+4x+1
c,x4+x3+2x2+2x+4
Bài 2. Cho hai đa thức: P(x) = 5x3 + 3 - 3x2 + x4 - 2x - 2 + 2x2 + x Q(x) = 2x4 + x2 + 2x + 2 - 3x2 - 5x + 2x3 - x4 a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến. b) Tính P(x) + Q(x), P(x) - Q(x), Q(x) - P(x)
ai giúp mình với:(
`@` `\text {Ans}`
`\downarrow`
`a)`
\(P(x) = 5x^3 + 3 - 3x^2 + x^4 - 2x - 2 + 2x^2 + x\)
`= x^4 + 5x^3 + (-3x^2 + 2x^2) + (-2x+x) + (3-2)`
`= x^4 + 5x^3 - x^2 - x + 1`
\(Q(x) = 2x^4 + x^2 + 2x + 2 - 3x^2 - 5x + 2x^3 - x^4\)
`= (2x^4 - x^4) + 2x^3 + (x^2 - 3x^2) + (2x-5x) + 2`
`= x^4 + 2x^3 - 2x^2 - 3x +2`
`b)`
`P(x)+Q(x) = (x^4 + 5x^3 - x^2 - x + 1) + (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 + x^4 + 2x^3 - 2x^2 - 3x +2`
`= (x^4+x^4)+(5x^3 + 2x^3) + (-x^2 - 2x^2) + (-x-3x) + (1+2)`
`= 2x^4 + 7x^3 - 3x^2 - 4x + 3`
`P(x)-Q(x)=(x^4 + 5x^3 - x^2 - x + 1) - (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 - x^4 - 2x^3 + 2x^2 + 3x -2`
`= (x^4 - x^4) + (5x^3 - 2x^3) + (-x^2+2x^2)+(-x+3x)+(1-2)`
`= 3x^3 + x^2 + 2x - 1`
`Q(x)-P(x) = (x^4 + 2x^3 - 2x^2 - 3x +2)-(x^4 + 5x^3 - x^2 - x + 1)`
`= x^4 + 2x^3 - 2x^2 - 3x +2-x^4 - 5x^3 + x^2 + x - 1`
`= (x^4-x^4)+(2x^3 - 5x^3)+(-2x^2+x^2)+(-3x+x)+(2-1)`
`= -3x^3 - x^2 - 2x + 1`
`@` `\text {Kaizuu lv u.}`
Giúp em với, em cảm ơn;;-;
Cho hai đa thức:
A(x) = 2x3 - x4 + 2x - 4 + 3x2 - 2x3 + x4
B(x) = x - 2
a) Thu gọn và sắp xếp đa thức A(x) theo lũy thừa giảm của biến
b) Thực hiện tính M(x)=A(x)+B(x)
N(x) = A(x) - B(x)
c) Tìm nghiệm của đa thức B(x)
`a,A(x) =2x^3 -x^4 +2x-4+3x^2 -2x^3+x^4`
`= ( 2x^3-2x^3) +(-x^4+x^4) + 2x -4+3x^2`
`= 0+0+ 2x -4+3x^2`
`= 3x^2 +2x-4`
`b, M(x)=A(x)+B(x)`
`M(x)= 3x^2 +2x-4 + x-2`
`= 3x^2 + 3x-6`
`b, N(x) = A(x) - B(x)`
`N(x)= 3x^2 +2x-4 -(x-2)`
`= 3x^2 +2x-4 -x+2`
`= 3x^2 + x -2`
`c,` Ta có :
`x-2=0`
`=> x=0+2`
`=>x=2`
Bài 1. Cho hai đa thức:
P(x) = 2x4 + 3x3 + 3x2 - x4 - 4x + 2 - 2x2 + 6x
Q(x) = x4 + 3x2 + 5x - 1 - x2 - 3x + 2 + x3
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính. P(x) + Q (x), P(x) - Q(x), Q(x) - P(x).
Bài 2. Cho hai đa thức:
P(x) = x5 + 5 - 8x4 + 2x3 + x + 5x4 + x2 - 4x3
Q(x) = (3x5 + x4 - 4x) - ( 4x3 - 7 + 2x4 + 3x5)
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm
dần của biến.
b) Tính P(x) + Q(x), P(x) - Q(x)
Bài 5. Cho hai đa thức:
P(x) = 2x4 + 2x3 - 3x2 + x +6
Q(x) = x4 - x3 - x2 + 2x + 1
a) Tính P(x) + Q(x), P(x) - Q(x)
b) Tính và P(x) - 2Q(x).
Bài 6. Cho đa thức P(x) = 2x4 - x2 +x - 2.
Tìm các đa thức Q(x), H(x), R(x) sao cho:
a) Q(x) + P(x) = 3x4 + x3 + 2x2 + x + 1
b) P(x) - H(x) = x4 - x3 + x2 - 2
c) R(x) - P(x) = 2x3 + x2 + 1
Bài 1: Phân tích các đa thức sau thành nhân tử
a)x2-y2-2x+2y e)x4+4y4
b)x2(x-1)+16(1-x) f)x4-13x2+36
c)x2+4x-y2+4 g) (x2+x)2+4x2+4x-12
d)x3-3x2-3x+1 h)x6+2x5+x4-2x3-2x2+1
a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$
cho 2 đa thức
P(x)=5x3+3-3x2+x4-2x-2+2x2+x
Q(x)=2x4+x2+2x+2-3x2-5x+2x3-x4
a)thu gọn và sắp xếp các hạng tử của 2 đa thức trên theo thứ tự giảm dần của biểu thức
b) tính P(x)-Q(x)
`a,`
`P(x)=5x^3+3-3x^2+x^4-2x-2+2x^2+x`
`P(x)=x^4+5x^3+(-3x^2+2x^2)+(-2x+x)+(3-2)`
`P(x)=x^4+5x^3-x^2-x+1`
`Q(x)=2x^4+x^2+2x+2-3x^2-5x+2x^3-x^4`
`Q(x)=(2x^4-x^4)+2x^3+(x^2-3x^2)+(2x-5x)+2`
`Q(x)=x^4+2x^3-2x^2-3x+2`
`b,`
`P(x)-Q(x)=(x^4+5x^3-x^2-x+1)-(x^4+2x^3-2x^2-3x+2)`
`P(x)-Q(x)= x^4+5x^3-x^2-x+1-x^4-2x^3+2x^2+3x-2`
`P(x)-Q(x)=(x^4-x^4)+(5x^3-2x^3)+(-x^2+2x^2)+(-x+3x)+(1-2)`
`P(x)-Q(x)=3x^3+x^2+2x-1`
Cho hai đa thức:
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1.
Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
= – x6 + x4 + (– 3x3 – x3) + (3x2 – 2x2) – 5
= – x6 + x4 – 4x3 + x2 – 5.
= – 5+ x2 – 4x3 + x4 – x6
Và Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1
= 2x5 – x4 + (x3 – 2x3) + x2 + x –1
= 2x5 – x4 – x3 + x2 + x –1.
= –1+ x + x2 – x3 – x4 + 2x5
Cho đa thức: f(x)=x4-3x2+2x-7 và g(x)=x+2
a) Thực hiện phép chia f(x) : g(x)
b) Tìm số nguyên x để f(x) chia hết cho g(x)
c) Tìm m để đa thức k(X)= -2x3+x-m chia hết cho g(x)
Lời giải:
a. $f(x)=x^4-3x^2+2x-7=x^3(x+2)-2x^2(x+2)+x(x+2)-7$
$=(x+2)(x^3-2x^2+x)-7=g(x)(x^3-2x^2+x)-7$
Vậy $f(x)$ chia $g(x)$ được thương là $x^3-2x^2+x$ và dư là $-7$
b. Theo phần a $f(x)=(x^3-2x^2+x)g(x)-7$
Với $x$ nguyên, để $f(x)\vdots g(x)$ thì $7\vdots g(x)$
$\Leftrightarrow x+2$ là ước của $7$
$\Rightarrow x+2\in\left\{\pm 1;\pm 7\right\}$
$\Leftrightarrow x\in\left\{-3; -1; 5; -9\right\}$
c.
Theo định lý Bezout về phép chia đa thức, để $K(x)=-2x^3+x-m\vdots x+2$ thì: $K(-2)=0$
$\Leftrightarrow -2(-2)^3+(-2)-m=0$
$\Leftrightarrow 14-m=0$
$\Leftrightarrow m=14$