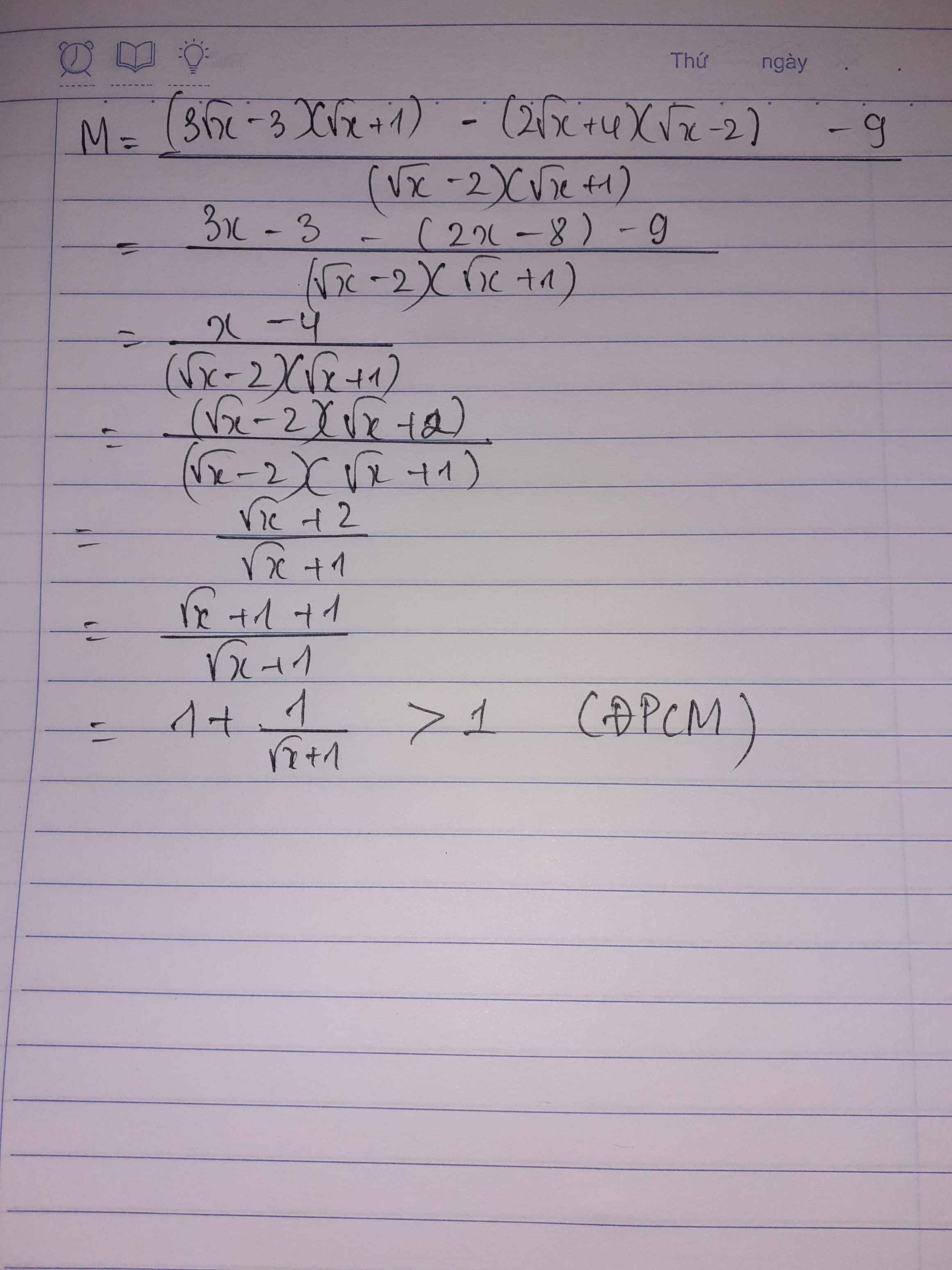Cho biểu thức: \(A=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\) với \(x\ge0;x\ne4\). Tìm các giá trị của x để \(A< \dfrac{-2}{3}\)
BB
Những câu hỏi liên quan
Cho A = \(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}+2}{\sqrt{x}-2}+\dfrac{2x+8}{2x-4}\) và B = \(\dfrac{2}{\sqrt{x}-6}\) với \(x\ge0;x\ne4;x\ne36\)
a) Rút gọn các biểu thức A
b) Tìm GTNN của biểu thức P = A : B
Bạn xem lại xem đã biết biểu thức đúng chưa vậy?
Đúng 0
Bình luận (0)
Cho A = \(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}+2}{\sqrt{x}-2}+\dfrac{2x+8}{2x-4}\) với \(x\ge0;x\ne4;x\ne36\)
Rút gọn biểu thức A
Sửa đề: x-4
\(A=\dfrac{x-2\sqrt{x}+x+4\sqrt{x}+4+2x+8}{x-4}=\dfrac{4x+2\sqrt{x}+12}{x-4}\)
Đúng 1
Bình luận (0)
Cho biểu thức \(A=\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\)với \(x\ge0,x\ne25\)
Biểu thức A sau khi rút gọn là A = \(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
1) So sánh A với 2
Có \(A=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}=1-\dfrac{10}{\sqrt{x}+5}\)
Dễ thấy \(\dfrac{10}{\sqrt{x}+5}>0\forall x\Rightarrow A=1-\dfrac{10}{\sqrt{x}+5}< 1\)
=> A < 2
Đúng 2
Bình luận (0)
Cho hai biểu thức:
A = \(\dfrac{\sqrt{x}}{\sqrt{x}+1}\) và B = \(\dfrac{7\sqrt{x}-6}{x-4}+\dfrac{\sqrt{x}-3}{\sqrt{x}+2}-\dfrac{1}{2-\sqrt{x}}\) (với \(x\ge0;x\ne4\))
c) Biểu thức B sau khi thu gọn được B = \(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\). Cho biểu thức P = A.B. Tìm x để \(\left|P\right|-P=0\)
\(P=A.B=\dfrac{\sqrt{x}}{\sqrt{x}+1}.\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Ta có : \(\left|P\right|-P=0\) \(\Leftrightarrow\left|P\right|=P\Leftrightarrow\left|\dfrac{\sqrt{x}}{\sqrt{x}-2}\right|=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(+TH_1:x\ge0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\) (luôn đúng)
\(+TH_2:x< 0\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}-2}=0\)
\(\Leftrightarrow-2.\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)=0\)
\(\Leftrightarrow x=0\)
Đúng 3
Bình luận (0)
Câu 1.Cho hai biểu thức Adfrac{sqrt{x}+2}{1+sqrt{x}} và Bleft(dfrac{2sqrt{x}}{x-sqrt{x}-6}+dfrac{sqrt{x}}{sqrt{x}-3}right):dfrac{sqrt{x}}{sqrt{x}-3} với xge0,xne9.1) Tính giá trị biểu thức A khi x 36.2) Rút gọn biểu thức B.3) Với x ∈ mathbb{Z}, tìm giá trị lớn nhất của biểu thức P A.B.Câu 2.Giải bài toán sau bằng cách lập hệ phương trình:Theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại. Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí n...
Đọc tiếp

Câu 1.
Cho hai biểu thức \(A=\dfrac{\sqrt{x}+2}{1+\sqrt{x}}\) và \(B=\left(\dfrac{2\sqrt{x}}{x-\sqrt{x}-6}+\dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\) với \(x\ge0,x\ne9\).
1) Tính giá trị biểu thức A khi x = 36.
2) Rút gọn biểu thức B.
3) Với x ∈ \(\mathbb{Z}\), tìm giá trị lớn nhất của biểu thức P = A.B.
Câu 2.
Giải bài toán sau bằng cách lập hệ phương trình:
Theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại. Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí nghiệp B hoàn thành vượt mức 10% so với kế hoạch. Do đó thực tế cả hai xí nghiệp làm được tổng cộng 800 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch?
Câu 3.
1) Giải phương trình: 3x4 - 2x2 - 40 = 0
2) Cho phương trình x2 + (m - 1)x - m2 - 2 = 0 (1), với m là tham số thực.
a) Chứng minh phương trình (1) luôn có hai nghiệm trái dấu x1, x2 với mọi giá trị của m.
b) Tìm m để biểu thức \(T=\left(\dfrac{x_1}{x_2}\right)^3+\left(\dfrac{x_2}{x_1}\right)^3\) đạt giá trị lớn nhất.
Câu 4.
Cho (O; R) và một điểm P nằm ngoài đường tròn. Kẻ hai tiếp tuyến PA, PB với đường tròn (A, B là tiếp điểm). Tia PO cắt đường tròn tại hai điểm K và I (K nằm giữa P và O) và cắt AB tại H. Gọi D là điểm đối xứng với B qua O, C là giao điểm của PD với đường tròn (O).
1) Chứng minh tứ giác BHCP nội tiếp.
2) Chứng minh PC.PD = PO.PH.
3) Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt BI tại Q. Chứng minh tam giác AQH cân.
4) Giả sử \(\widehat{BDC}=45^o\). Tính diện tích tam giác PBD phần nằm bên ngoài đường tròn (O) theo R.
Câu 5.
Tìm m để phương trình ẩn x sau đây có ba nghiệm phân biệt. x3 - 2mx2 + (m2 + 1)x - m = 0.
Câu 1:
a) ĐKXĐ: \(x>0;x\ne9\)
Với x=36 (thỏa mãn ĐKXĐ) thì A có giá trị :
\(A=\dfrac{\sqrt{36}+2}{1+\sqrt{36}}=\dfrac{6+2}{1+6}=\dfrac{8}{7}\)
b) Ta có:
\(B=\left(\dfrac{2\sqrt{x}}{x-\sqrt{x}-6}+\dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}=\dfrac{2\sqrt{x}+\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}=\dfrac{x+4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+4}{\sqrt{x}+2}\)
c) Ta có:
\(P=A\cdot B=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}+4}{\sqrt{x}+2}=\dfrac{\sqrt{x}+4}{\sqrt{x}+1}=1+\dfrac{3}{\sqrt{x}+1}\)
Vì x là số nguyên lớn hơn 0 nên
\(x\ge1\Rightarrow\sqrt{x}\ge1\Rightarrow\sqrt{x}+1\ge2>0\Rightarrow P\le1+\dfrac{3}{2}=\dfrac{5}{2}\)
Dấu bằng xảy ra khi x=1;
Đúng 5
Bình luận (0)
Gọi số sản phẩm dự định của xí nghiệp A và B lần lượt là x,y \(\left(x,y\in N;0< x,y< 720\right)\)
Vì tổng sản phẩm dự định là 720 nên ta có phương trình: \(x+y=720\left(1\right)\)
Vì thực tế , xí nghiệp A hoàn thành vượt mức 12% nên số sản phẩm xí nghiệp A thực tế là : \(112\%x=\dfrac{28}{25}x\)
Xí nghiệp B hoàn thành vượt mức 10% nên số sản phẩm xí nghiệp B thực tế là : \(110\%y=\dfrac{11}{10}y\)
Vì tổng số sản phẩm thực tế là 800 nên ta có phương trình: \(\dfrac{28}{25}x+\dfrac{11}{10}y=800\Leftrightarrow56x+55y=40000\left(2\right)\)
Từ (1)(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=720\\56x+55y=40000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=720\\55\cdot720+x=40000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=400\\y=320\end{matrix}\right.\left(t.m\right)\)
Vậy số sản phẩm 2 xí nghiệp làm theo kế hoạch lần lượt là 400 và 320 sản phẩm
Đúng 3
Bình luận (0)
1) Ta có phương trình:
\(3x^4-2x^2-40=0\Leftrightarrow\left(3x^4-12x^2\right)+\left(10x^2-40\right)=0\Leftrightarrow\left(x^2-4\right)\left(3x^2+10\right)=0\)
Mà \(3x^2+10\ge10>0\)
\(\Leftrightarrow x^2-4=0\Leftrightarrow x^2=4\Leftrightarrow x=\pm2\)
Vậy \(S=\left\{\pm2\right\}\) là tập nghiệm của phương trình
2)
Xét phương trình bậc 2 ẩn x :
\(x^2+\left(m-1\right)x-m^2-2=0\left(1\right)\)
Có hệ số: \(a=1;b=m-1;c=-m^2-2\)
\(\Rightarrow ac=-m^2-2\le-2< 0\)
Suy ra (1) có 2 nghiệm trái dấu \(x_1,x_2\) với mọi m thỏa mãn:
\(\left\{{}\begin{matrix}x_1+x_2=1-m\\x_1x_2=-m^2-2\end{matrix}\right.\left(2\right)\)
Đặt \(\left(\dfrac{x_1}{x_2}\right)^3=-a\left(a>0\right)\Rightarrow\left(\dfrac{x_2}{x_1}\right)^3=-\dfrac{1}{a}\) (do x1,x2 là 2 số trái dấu)
\(\Rightarrow T=-\left(a+\dfrac{1}{a}\right)\)
Áp dụng bất đẳng thức Cô-si cho 2 số dương \(a\) và \(\dfrac{1}{a}\) ta có:
\(a+\dfrac{1}{a}\ge2\sqrt{a\cdot\dfrac{1}{a}}=2\)
\(\Rightarrow T\le-2\)
Dấu "=" xảy ra \(\Leftrightarrow a=\dfrac{1}{a}\Leftrightarrow a=1\left(a>0\right)\Leftrightarrow x_1=-x_2\)
(2) trở thành: \(\left\{{}\begin{matrix}m-1=0\\x_1^2=m^2+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=1\\x_1^2=3\left(t.m\right)\end{matrix}\right.\)
Vậy T đạt giá trị nhỏ nhất là -2 tại m=1
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Cho các biểu thức sau:
A = \(\dfrac{x+3}{\sqrt{x}+1}\) và B = \(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{2\sqrt{x}}{1-x}\) với \(x\ge0;x\ne1\)
a) Rút gọn các biểu thức B
b) Cho \(P=B:A\). Với \(x>1\), tìm GTNN của biểu thức \(\dfrac{1}{P}\)
a.
\(B=\dfrac{\sqrt{x}+1+\sqrt{x}\left(\sqrt{x}-1\right)+2\sqrt{x}}{1-x}=\dfrac{\sqrt{x}+1+x-\sqrt{x}+2\sqrt{x}}{1-x}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b.
\(P=\dfrac{B}{A}=\dfrac{x+3}{\sqrt{x}+1}:\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\left(x+3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{x+3}{\sqrt{x}-1}=\dfrac{x-1+4}{\sqrt{x}-1}\)
\(=\sqrt{x}+1+\dfrac{4}{\sqrt{x}-1}\)\(=\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}+2\)
Theo BĐT AM - GM ta có: \(\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}\ge2\sqrt{\left(\sqrt{x}-1\right)\dfrac{4}{\sqrt{x}-1}}=4\)
\(\Rightarrow\dfrac{1}{P}\ge6\Rightarrow Min_{\dfrac{1}{P}}=6\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=4\Rightarrow x=9\) (loại trường hợp \(\sqrt{x}-1=-2\))
Vậy GTNN của biểu thức \(\dfrac{1}{P}=6\) khi x = 9.
Đúng 2
Bình luận (1)
cho biểu thức \(M=\dfrac{3\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+4}{\sqrt{x}+1}-\dfrac{9}{x-\sqrt{x}-2}\),(với \(x\ge0,x\ne4\))chứng minh A>1
Ta có: \(M=\dfrac{3\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+4}{\sqrt{x}+1}-\dfrac{9}{x-\sqrt{x}-2}\)
\(=\dfrac{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x-3-2x+8-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
Ta có: \(A-1=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-1\)
\(=\dfrac{\sqrt{x}+2-\sqrt{x}-1}{\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ
hay A>1
Đúng 1
Bình luận (0)
\(M=\dfrac{3\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+4}{\sqrt{x}+1}-\dfrac{9}{x-\sqrt{x}-2}\\ =\dfrac{3\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}-\dfrac{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{9}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{3\left(x-1\right)-2\left(x-4\right)-9}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}=\dfrac{x-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{\sqrt{x}+2}{\sqrt{x}+1}=1+\dfrac{1}{\sqrt{x}+1}>1\)
Đúng 1
Bình luận (0)
Cho biểu thức A dfrac{sqrt{x}}{sqrt{x}-5}-dfrac{10sqrt{x}}{x-25}-dfrac{5}{sqrt{x}+5} với xge0,xne25.Biểu thức A sau khi rút gọn là: dfrac{sqrt{x}-5}{sqrt{x}+5}2) Tìm giá trị nhỏ nhất của A
Đọc tiếp
Cho biểu thức A = \(\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\) với \(x\ge0,x\ne25\).
Biểu thức A sau khi rút gọn là: \(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
2) Tìm giá trị nhỏ nhất của A
2: \(A=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}=\dfrac{\sqrt{x}+5-10}{\sqrt{x}+5}\)
\(=1-\dfrac{10}{\sqrt{x}+5}\)
\(\sqrt{x}+5>=5\forall x\)
=>\(\dfrac{10}{\sqrt{x}+5}< =\dfrac{10}{5}=2\forall x\)
=>\(-\dfrac{10}{\sqrt{x}+5}>=-2\forall x\)
=>\(-\dfrac{10}{\sqrt{x}+5}+1>=-2+1=-1\forall x\)
Dấu '=' xảy ra khi x=0
Vậy: \(A_{min}=-1\) khi x=0
Đúng 1
Bình luận (0)
Cho biểu thức A = \(\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\) với \(x\ge0,x\ne25\).
Biểu thức A sau khi rút gọn là: \(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
1) Tìm các giá trị của x để A = \(\dfrac{2\sqrt{x}}{3}\)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\left(x\ge0;x\ne25\right)\)
Để \(A=\dfrac{2\sqrt{x}}{3}\) thì:
\(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}=\dfrac{2\sqrt{x}}{3}\)
\(\Leftrightarrow3\sqrt{x}-15=2x+10\sqrt{x}\)
\(\Leftrightarrow2x+10\sqrt{x}-3\sqrt{x}+15=0\)
\(\Leftrightarrow2x+7\sqrt{x}+15=0\)
Mà \(2x+7\sqrt{x}+15>0\) (vì \(x\ge0\))
nên không tìm được giá trị nào của \(x\) thoả mãn \(A=\dfrac{2\sqrt{x}}{3}\)
#\(Toru\)
Đúng 2
Bình luận (0)
Câu 1.Cho các biểu thức Adfrac{25sqrt{x}+6}{x-36}-dfrac{sqrt{x}-1}{6-sqrt{x}}+dfrac{2sqrt{x}}{sqrt{x}+6} và Bdfrac{x-6sqrt{x}}{sqrt{x}-1} với xge0;xne1;xne36a) Tính giá trị của biểu thức B khi x 16.b) Rút gọn biểu thức A.c) Đặt T sqrt{A.B}. Tìm giá trị nhỏ nhất của biểu thức T.Câu 2.Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:Hôm chủ nhật trước, Dũng được bố chở bằng xe máy đi về quê cách nhà 60 km với vận tốc dự định. Trên đường về do có dfrac{1}{3} quãng đường là đường...
Đọc tiếp

Câu 1.
Cho các biểu thức \(A=\dfrac{25\sqrt{x}+6}{x-36}-\dfrac{\sqrt{x}-1}{6-\sqrt{x}}+\dfrac{2\sqrt{x}}{\sqrt{x}+6}\) và \(B=\dfrac{x-6\sqrt{x}}{\sqrt{x}-1}\) với \(x\ge0;x\ne1;x\ne36\)
a) Tính giá trị của biểu thức B khi x = 16.
b) Rút gọn biểu thức A.
c) Đặt T = \(\sqrt{A.B}.\) Tìm giá trị nhỏ nhất của biểu thức T.
Câu 2.
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hôm chủ nhật trước, Dũng được bố chở bằng xe máy đi về quê cách nhà 60 km với vận tốc dự định. Trên đường về do có \(\dfrac{1}{3}\) quãng đường là đường xấu nên để đảm bảo an toàn, bố bạn đã phải giảm bớt vận tốc đi 10 km/h, do đó đã về tới quê chậm nhất 10 phút so với dự kiến. Tính vận tốc dự định của hai bố con bạn Dũng.
Câu 3.
1) Giải hệ phương trình: \(\left\{{}\begin{matrix}2\sqrt{x-1}+\dfrac{14}{2y+1}=10\\\sqrt{x-1}-\dfrac{5}{2y+1}=\dfrac{23}{7}\end{matrix}\right.\)
2) Cho phương trình \(x^2-2\left(m+5\right)x+2m+9=0\)
a) Giải phương trình với m = 10.
b) Tìm m để phương trình có hai nghiệm x1; x2 thỏa mãn điều kiện: x1 - 2 \(\sqrt{x_2}=0\).
Câu 4.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh AEHF, BCEF là các tứ giác nội tiếp.
b) Kẻ đường kính AM của (O). Chứng minh BHCM là hình bình hành và AB.AC = AM.AD.
c) Cho BC cố định, A di động trên cung lớn BC sao cho ABC có ba góc nhọn; BE cắt (O) tại I. CF cắt (O) tại J. Chứng minh đoạn IJ có độ dài không đổi.
Câu 1:
a) Khi x =16 (t.m ĐKXĐ) thì B có giá trị là:
\(B=\dfrac{16-6\cdot4}{4-1}=\dfrac{-8}{3}\)
b) Ta có:
\(A=\dfrac{25\sqrt{x}+6}{x-36}-\dfrac{\sqrt{x}-1}{6-\sqrt{x}}+\dfrac{2\sqrt{x}}{\sqrt{x}+6}=\dfrac{25\sqrt{x}+6}{\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)}+\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}-6\right)}{\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)}=\dfrac{25\sqrt{x}+6+x+5\sqrt{x}-6+2x-12\sqrt{x}}{\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)}=\dfrac{3x+18\sqrt{x}}{\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-6}\)
c) Ta có:
\(T=\sqrt{A\cdot B}=\sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}-6}\cdot\dfrac{x-6\sqrt{x}}{\sqrt{x}-1}}=\sqrt{\dfrac{3x\left(\sqrt{x}-6\right)}{\left(\sqrt{x}-6\right)\left(\sqrt{x}-1\right)}}=\sqrt{\dfrac{3\left(x-1\right)+3}{\sqrt{x}-1}}=\sqrt{3\left(\sqrt{x}+1\right)+\dfrac{3}{\sqrt{x}-1}}=\sqrt{3\left(\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}\right)+6}\overset{Cosi}{\ge}\sqrt{3\cdot2+6}=2\sqrt{3}\)
Dấu = xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=1\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\left(t.m\right)\)
Đúng 5
Bình luận (0)
Gọi vận tốc dự định của hai bố con bạn Dũng là x(km/h)(x>0).Đổi: 10 phút =\(\dfrac{1}{6}\)(h)
thời gian dự định đi về quê là \(\dfrac{60}{x}\)(h)
vận tốc đi trên \(\dfrac{1}{3}\)quãng đường là đường xấu hai bố con bạn Dũng là \(x-10\)(km/h)
Thời gian thực tế đi về quê là \(\dfrac{\dfrac{1}{3}\cdot60}{x-10}+\dfrac{\dfrac{2}{3}\cdot60}{x}\)(h)
Vì hai bố con bạn Dũng đã về tới quê chậm mất 10 phút so với dự kiến
Nên ta có pt sau:
\(\left(\dfrac{\dfrac{1}{3}\cdot60}{x-10}+\dfrac{\dfrac{2}{3}\cdot60}{x}\right)-\dfrac{1}{6}=\dfrac{60}{x}\)
⇔\(\dfrac{20}{x-10}+\dfrac{40}{x}-\dfrac{1}{6}=\dfrac{60}{x}\)
⇔\(20x+40\left(x-10\right)-\dfrac{1}{6}x\left(x-10\right)=60\left(x-10\right)\)
⇔\(-\dfrac{1}{6}x^2+\dfrac{5}{3}x+200=0\)
⇒\(\left[{}\begin{matrix}x=40\left(n\right)\\x=-30\left(l\right)\end{matrix}\right.\)
Vậy ......
Đúng 2
Bình luận (0)
Gọi x(km/h)x(km/h) là vận tốc dự định của hai bố con (x>10)(x>10)
Thời gian dự định là: 60x60x (giờ)
1313 quãng đường là: 13.60=20(km)13.60=20(km)
Vận tốc trên đoạn đường 20km20km là: x−10(km/h)x−10(km/h)
Thời gian đi trên đoạn đường 20km20km là: 20x−1020x-10 (giờ)
Đoạn đường đi với vận tốc dự định là: 60−20=40(km)60-20=40(km)
Thời gian đi trên đoạn đường 40km40km là: 40x40x (giờ)
Vì hai bố con về tới quê chậm 1010 phút =16=16 giờ nên ta có phương trình sau:
60x+16=20x−10+40x 60x+16=20x-10+40x
⇔20x+16−20x−10=0⇔20x+16-20x-10=0
⇔20.6(x−10)+1.x(x−10)−20.6x=0⇔20.6(x-10)+1.x(x-10)-20.6x=0
⇔120x−1200+x2−10x−120x=0⇔120x-1200+x2-10x-120x=0
⇔x2−10x−1200=0⇔x2-10x-1200=0
⇔⇔[x=−30(loại)x=40(thỏa mãn)[x=−30(loại)x=40(thỏa mãn)
Vậy vận tốc dự định của hai bố con là 40km/h
Đúng 1
Bình luận (0)
Xem thêm câu trả lời