Câu 20: Tam giác ABC vuông tại B suy ra:

   A.  AC²  = AB² + BC^{2 ­}                                   B.  AC²  = AB² - BC²

   C.  BC²  = AB² + AC²                                    D.  AB²  = BC² + AC²

Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?

   A.  Tại  B                                                      B.  Tại C

   C.  Tại A                                                       D.  Không phải là tam giác vuông

Câu 22: Cho ABC có  = 90⁰ ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:

   A.  6,5 cm                    B.  5,5 cm                     C.  6 cm                       D.   6,2 cm

Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:

A.  3cm, 4dm, 5cm.         B.  5cm, 14cm, 12cm. 

C.  5cm, 5cm, 8cm.         D.  9cm, 15cm, 12cm.

Câu 24: Cho ABC có  AB = AC và  = 60⁰, khi đó tam giác ABC là:

   A.  Tam giác vuông                                       B.   Tam giác cân

   C.  Tam giác đều                                           D.  Tam giác vuông cân

Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:

A.  ∠A ≤ 90⁰                                 B. ∠A > 90⁰                            C. ∠A < 90⁰                       D. ∠A = 90⁰

-Kẻ đường phân giác AD của △ABC.

-Có: \(\widehat{ADC}=\widehat{BAD}+\widehat{ABD}\) (\(\widehat{ADC}\) là góc ngoài của △ABD)

\(\widehat{BAC}=\widehat{BAD}+\widehat{CAD}\)

Mà \(\widehat{ABD}=\widehat{CAD}\left(=\dfrac{1}{2}\widehat{BAC}\right)\)

\(\Rightarrow\widehat{ADC}=\widehat{BAC}\)

-Xét △ADC và △BAC có:

\(\widehat{ADC}=\widehat{BAC}\left(cmt\right)\)

\(\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△ADC∼△BAC (g-g).

\(\Rightarrow\dfrac{DC}{AC}=\dfrac{AC}{BC}\)(tỉ số đồng dạng)

-Xét △ABC có: AD là phân giác (gt)

\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\) (định lí đường phân giác của tam giác)

\(\Rightarrow\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}\)

\(\Rightarrow CD=\dfrac{BC.AC}{AB+AC}\)

Mà \(\dfrac{DC}{AC}=\dfrac{AC}{BC}\left(cmt\right)\)

\(\Rightarrow\dfrac{\dfrac{BC.AC}{AB+AC}}{AC}=\dfrac{AC}{BC}\)

\(\Rightarrow\dfrac{BC}{AB+AC}=\dfrac{AC}{BC}\)

\(\Rightarrow\left(AB+AC\right).AC=BC^2\)

\(\Rightarrow AC^2+AB.AC=BC^2\)

A

a, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{BC}^2\)

\(\Leftrightarrow AC^2+AB^2-2\overrightarrow{AB}.\overrightarrow{AC}=BC^2\)

\(\Leftrightarrow2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\)

\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}=\dfrac{5^2+8^2-7^2}{2}=20\)

b, \(2\overrightarrow{CA}.\overrightarrow{CB}=CA^2+CB^2-BC^2=CA^2\)

\(\Rightarrow\overrightarrow{CA}.\overrightarrow{CB}=\dfrac{CA^2}{2}=\dfrac{8^2}{2}=32\)

Lời giải:

a) 

\(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\)

\(\Rightarrow (\overrightarrow{AC}-\overrightarrow{AB})^2=\overrightarrow{BC}^2\Leftrightarrow AB^2+AC^2-2\overrightarrow{AC}.\overrightarrow{AB}=BC^2\)

\(\Leftrightarrow 2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\) (đpcm)

Ta có:

\(\overrightarrow{AB}.\overrightarrow{AC}=\frac{AB^2+AC^2-BC^2}{2}=\frac{5^2+8^2-7^2}{2}=20\)

\(\cos \angle A=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|}=\frac{20}{5.8}=\frac{1}{2}\)

\(\Rightarrow \angle A=60^0\)

b) 

Tương tự phần a, \(\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-AB^2}{2}=\frac{8^2+7^2-5^2}{2}=44\)

a, Sử dụng định lí Pytago cho các tam giác vuông HAB và HAC để có đpcm

b, 1. Chứng minh tương tự câu a)

2. Sử dụng định lí Pytago cho tam giác vuông AHM

Đáp án: D

a sai vì nếu tam giác ABC thỏa mãn AB²  + AC² = BC² thì tam giác ABC vuông tại A không phải vuông tại B.

b, c, d đúng.

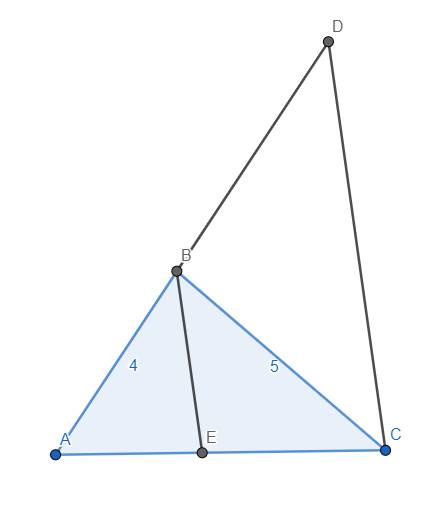
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.

b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)

Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\)  nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\),  suy ra \(AD=AB+BD=4+5=9\).

\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).

Vậy \(AC=6\)

 Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.

Lê Song Phương: \(\dfrac{EA}{EC}=\dfrac{BA}{BC}\) em lấy từ đâu ra vậy em?

Không có trong đề bài, vì vậy trước khi khẳng định mặt khác:

                             \(\dfrac{EA}{EC}\) = \(\dfrac{BA}{BC}\)

thì em cần chứng minh điều đó đã