Cho tam giác MON vuông ở O. Lấy điểm P trên cạnh OM, Q trên cạnh ON. Chứng minh PQ < MQ < MN
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Cho tam giác OMN vuông tại O. Lấy điểm P trên cạnh OM, điểm Q trên cạnh ON. Chứng minh PQ < MQ < MN?
Cho tam giác OMN vuông tại O. Lấy điểm P trên cạnh OM, điểm Q trên cạnh ON. Chứng minh PQ < MQ < MN? (Giải chi tiết)
Cho tam giác OMN vuông tại O. Lấy điểm P trên cạnh OM, điểm Q trên cạnh ON. Chứng minh PQ < MQ < MN? (Giải chi tiết)
cho tam giác mnp vuông tại m (mp<mn) trên cạnh mn lấy điểm q sao cho mq=mp trên tia đối của tia mp lấy điểm r sao cho mr=mn chứng minh :
a) pq vuông góc nr b) rq vuông góc np
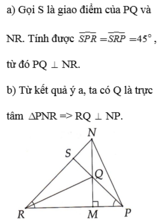
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Chứng minh:
a) P Q ⊥ N R .
b) R Q ⊥ N P .
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho MN song song PQ và khoảng cách giữa MN và PQ bằng độ dài AB.
a. Chứng minh MP là phân giác góc QMN;
b. Gọi O là giao điểm của MQ và NP. Tính số đo góc MON
Cho tam giác OBC cân tại O , Gọi A là trung điểm BC . Trên cạnh OB lấy điểm M , cạnh OC lấy điểm N sao cho OM= ON. Chứng minh rằng :
a) OA vuông góc BC
b) MN song song BC
Xem chi tiết
a) Xét tam giác OBC cân tại O có:
OA là trung tuyến (A là trung điểm BC)
=> OA là đường cao (TC các đường trong tam giác cân)
=> OA vuông góc BC (đpcm)
b) Xét tam giác OBC cân tại O có:
OA là trung tuyến (A là trung điểm BC)
=> OA là đường phân giác ^A (TC các đường trong tam giác cân)
Xét tam giác OMN có: OM = ON (gt)
=> Tam giác OMN cân tại O
Mà OA là đường phân giác ^A (cmt)
=> OA là đường cao (TC các đường trong tam giác cân)
=> OA vuông góc MN
Mà OA vuông góc BC (cmt)
=> MN // BC (Từ vuông góc đến //)
Đúng 1
Bình luận (0)
Bài 4: (6 điểm) Cho hình vuông ABCD có 2 đường chéo AC và BD cắt nhau tại O. Trêncạnh AB lấy M ( 0MBMA) và trên cạnh BC lấy N sao cho góc MON 90 độ. Gọi E là giao điểm của AN và DC, gọi K là giao điểm của ON,BE. Chứng minh:1.Tam giác MONvuông cân2. Chứng minh MN song song với BE3. Chứng minh CK vuông góc với BE4. Qua K vẽ đường song song với OM cắt BC tại H. Chứng minh KC/KB + KN/KH + CN/BH 1.
Đọc tiếp
Bài 4: (6 điểm) Cho hình vuông ABCD có 2 đường chéo AC và BD cắt nhau tại O. Trên
cạnh AB lấy M ( 0<MB<MA) và trên cạnh BC lấy N sao cho góc MON = 90 độ. Gọi E là giao điểm của AN và DC, gọi K là giao điểm của ON,BE.
Chứng minh:
1.Tam giác MON
vuông cân
2. Chứng minh MN song song với BE
3. Chứng minh CK vuông góc với BE
4. Qua K vẽ đường song song với OM cắt BC tại H. Chứng minh KC/KB + KN/KH + CN/BH =1.
Bài 5. Cho tam giác MNP có MN MP. Gọi I là trung điểm của cạnh NP. a)CMR: tam giác MNItam giác MPI, từ đó chứng minh MI vuông góc với NP. b)Trên tia đối của tia IM lấy điểm Q sao cho IQ IM. CMR: MN // PQ. c)Lấy điểm E trên MN và điểm F trên PQ sao cho ME QF. Chứng minh rằng: Ba điểm E, I, F thẳng hàng.mik đang càn gaaso :((
Đọc tiếp
Bài 5. Cho tam giác MNP có MN = MP. Gọi I là trung điểm của cạnh NP.
a)CMR: tam giác MNI=tam giác MPI, từ đó chứng minh MI vuông góc với NP.
b)Trên tia đối của tia IM lấy điểm Q sao cho IQ = IM. CMR: MN // PQ.
c)Lấy điểm E trên MN và điểm F trên PQ sao cho ME = QF. Chứng minh rằng: Ba điểm E, I, F thẳng hàng.
mik đang càn gaaso :((
a: Xét ΔMNI và ΔMPI có
MN=MP
NI=PI
MI chung
Do đó: ΔMNI=ΔMPI
Ta có: ΔMNP cân tại M
mà MI là đường trung tuyến
nên MI là đường cao
b: Xét tứ giác MNQP có
I là trung điểm của MQ
I là trung điểm của NP
Do đó: MNQP là hình bình hành
Suy ra: MN//PQ
c: Xét tứ giác MEQF có
ME//QF
ME=QF
Do đó: MEQF là hình bình hành
Suy ra: MQ và EF cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của MQ
nên I là trung điểm của FE
hay E,I,F thẳng hàng
Đúng 2
Bình luận (0)