PV
Những câu hỏi liên quan
Cho tam giác ABC có ba cạnh a,b,c. Chứng minh rằng:
\(\dfrac{a^2+b^2+c^2}{2abc}=\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
Đúng 1
Bình luận (0)
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
Đúng 0
Bình luận (0)
Chứng minh rằng trong mọi tam giác ABC ta đều có:
a, a = b cosC + c cosB;
b, sinA = sinBcosC + sinCcosB;
c, ha = 2RsinBsinC.
a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
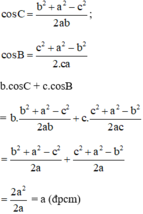
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
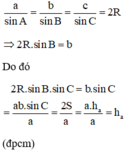
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, BC = a, CA = b, AB = c. Chứng minh rẳng:
a = b. cosC + c. cosB.
Áp dụng hệ quả của định lý Cosin ta có:
\(\cos C=\dfrac{b^2+a^2-c^2}{2ab};\cos B=\dfrac{c^2+a^2-b^2}{2ca}\)
\(\Rightarrow b\cos C+c\cos B=b\dfrac{b^2+a^2-c^2}{2ab}+c\dfrac{c^2+a^2-b^2}{2ca}=\)
\(\dfrac{b^2+a^2-c^2}{2a}+\dfrac{c^2+a^2-b^2}{2a}=\dfrac{2a^2}{2a}=a\)
Đúng 0
Bình luận (0)
Tam giác ABC Có A=120 ° b=6, c=4, tìm cạnh a và góc B, C
Xem chi tiết
a2 = b2 + c2 - 2bc.cos1200
⇔ a2 = 76
⇔ a = \(2\sqrt{19}\)
Theo định lí sin: \(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\)
⇔ \(\dfrac{2\sqrt{19}}{sin120}=\dfrac{6}{sinB}=\dfrac{4}{sinC}\)
⇔ \(\left\{{}\begin{matrix}sinC=\dfrac{\sqrt{57}}{19}\\sinB=\dfrac{3\sqrt{57}}{38}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=36^035'\\\widehat{C}=23^025'\end{matrix}\right.\)
Đúng 1
Bình luận (3)
cho tam giác ABC thoả mãn
a, \(\dfrac{1+cosB}{1-cosB}\)= \(\dfrac{2a+c}{2a-c}\) CM: tam giác cân
b, tanB.tanC = \(\dfrac{tanA}{sinB.sinC}\) CM: tam giác vuông
c, \(\left\{{}\begin{matrix}\dfrac{1+cosC}{sinC}=\dfrac{2a+b}{\sqrt{4a^2-b^2}}\\a^2\left(b+c-a\right)=b^3+c^3-a^3\end{matrix}\right.\) CM: tam giác đều
Cho tam giác nhọn ABC, BC = a, CA = b, AB = c. Chứng minh rẳng:
a = b. cosC + c. cosB.
: Tam giác ABC vuông tại A. Khẳng định nào sau đây đúng?
A. sinB = sinC B. cosB = cosC C. tanB = cotC D. cotB = cotC
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
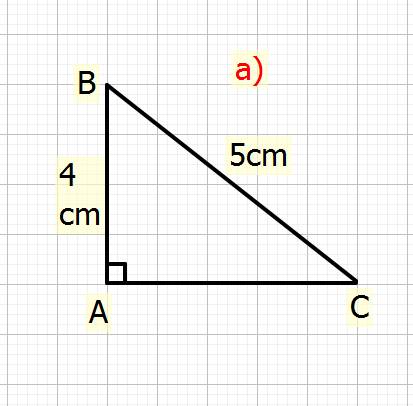
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
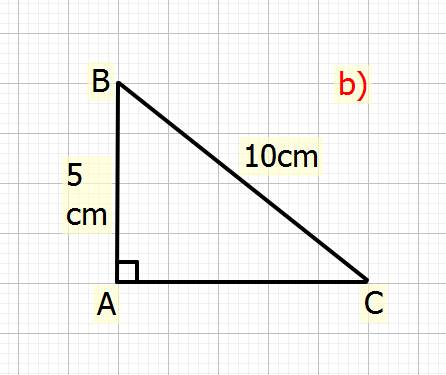
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)