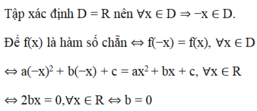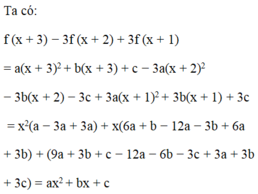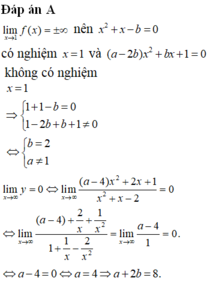Tìm điều kiện của tham số m để hàm số f(x) = a x 2 + bx + c là hàm số chẵn
A. a tùy ý, b = 0, c = 0
B. a tùy ý, b = 0, c tùy ý
C. a, b, c tùy ý
D. a tùy ý, b tùy ý, c = 0
Cho hàm số y = f(x) = a x 2 + bx + c. Rút gọn biểu thức f (x + 3) – 3f(x + 2) + 3f(x + 1) ta được:
A. a x 2 – bx – c
B. a x 2 + bx – c
C. a x 2 – bx + c
D. a x 2 + bx + c
Cho tam thức bậc hai f(x) = a x 2 + bx + c, (a ≠ 0) có biệt thức Δ = b 2 - 4ac. Chọn khẳng định đúng:
A. Nếu Δ < 0 thì af(x) > 0, ∀x ∈ R
B. Nếu Δ > 0 thì af(x) < 0, ∀x ∈ R
C. Nếu Δ ≤ 0 thì af(x) ≥ 0, ∀x ∈ R
D. Nếu Δ ≥ 0 thì af(x) > 0, ∀x ∈ R
Đáp án A.
Ta có: nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a với mọi giá trị của x, tức là af(x) > 0, ∀x ∈ R
Cho đa thức f(x)=(x2 - bx) (2x + b) có hệ số của x2 là 5, tìm giá trị của f(1)
f(x) = (x² - bx)(2x + b)
= 2x³ + bx² - 2bx² - b²x
= 2x³ - bx² - b²x
Do hệ số của x² là 5
⇒ -b = 5
⇒ b = -5
f(x) = 2x³ + 5x² - 25x
f(1) = 2.1³ + 5.1² - 25.1
= -18
Tìm hệ số a,b,c biết
a, −3x2(2ax2−bx+c)=6x5+9x4−3c2∀x−3x2(2ax2−bx+c)=6x5+9x4−3c2∀x
b,(x2+cx+2)(a+b)=x3+x2−2∀x(x2+cx+2)(a+b)=x3+x2−2∀x
c,(ax2+bx+c)+(x+3)=x2+2x−3x∀x(ax2+bx+c)+(x+3)=x2+2x−3x∀x
Help me!!
bạn ghi lại đề đi mình chả hiểu cái mô tê gì cả
Biết hàm số f ( x ) = ( a - 2 b ) x 2 + b x + 1 x 2 + x - b có lim x → 1 f ( x ) = ± ∞ và lim x → 1 f ( x ) = 0 Tính a + 2b
A. 8
B. 7
C. 6
D. 10
Cho f(x)=ax^2+bx+c xác định a b c biết đa thức có hai nghiệm là x1=1 x2=2
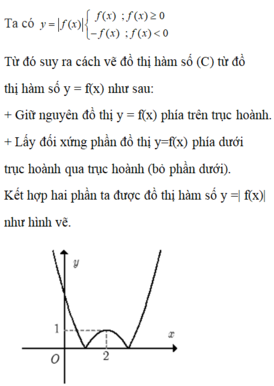
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.
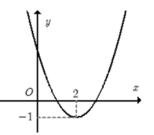
A. 0 < m < 1.
B. m > 3.
C. m = −1, m = 3.
D. −1 < m < m 0 .
Tìm a, b, để f(x) = x3+ax2-bx+12 chia hết cho g(x) = x2+x-6
Tìm a, b để f(x) = x3+ax2+bx-2 chia hết cho g(x) =
x2+1
Đa thức \(g\left(x\right)=x^2+x-6\)có nghiệm \(\Leftrightarrow x^2+x-6=0\)
\(\Leftrightarrow x^2+2x-3x-6=0\Leftrightarrow x\left(x+2\right)-3\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)
Để đa thức f(x) = x3+ax2-bx+12 chia hết cho g(x) = x2+x-6 thì 3 và -2 cũng là hai nghiệm của đa thức x3+ax2-bx+12
Nếu x = 3 thì \(f\left(3\right)=27+9a-3b+12=0\)
\(\Leftrightarrow9a-3b=-39\Leftrightarrow3a-b=-13\)(1)
Nếu x = -2 thì \(f\left(-2\right)=-8+4a+2b+12=0\)
\(\Leftrightarrow4a+2b=-4\Leftrightarrow2a+b=-2\)(2)
Lấy (1) + (2), ta được: \(5a=-15\Leftrightarrow a=-3\)
\(\Rightarrow b=-2+3.2=4\)
Vậy a= -3; b = 4
Để f(x) = x3+ax2+bx-2 chia hết cho g(x) =x2+1 thì \(\left(b-1\right)x-\left(a+2\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}b-1=0\\a+2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\a=-2\end{cases}}\)
