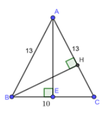
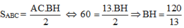Cho tam giác ABC cân tại A, có AB=13cm;BC=10cm. Kẻ AH vuông góc BC (H thuộc BC)
a) Chứng minh HB=HC và tính AH.
b) Đường trung tuyến BD của tam giác ABC cắt AH tại G. Tính độ dài đoạn thẳng AG và BD.
c) Chứng minh tam giác BGC cân.
d) Từ B kẻ đường thẳng vuông góc với AB, đường thẳng này cắt đoạn thẳng A C tại E. Trên cạnh AE lấy điểm F sao cho EB= E F. Chứng minh góc CPF=1/2 ABE