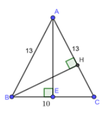
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
![]()
![]()
Mặt khác:
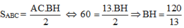
Xét ABH vuông tại H có:
![]()
Đáp án cần chọn là: A

Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
![]()
![]()
Mặt khác:
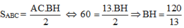
Xét ABH vuông tại H có:
![]()
Đáp án cần chọn là: A
Cho tam giác ABC vuông tại A có ,AB =5cm AC = 12cm ,BC = 13cm a)Tính sin B b) tính sin C c) tính số đo gốc B và C
Cho tam giác ABC vuông tại C. Kẻ đường cao CH
a) Cho AB= 13cm, BH= 5cm. Tính sin B, sin A
b) Cho CH= 10cm, CA= 12,5cm. Tính cos A, tan B
c) Cho AH= 12cm, BH= 8cm. Tính sin A, cot B
Cho tam giác ABC cân tại A có AB = 10, BC = 12.
a) Tính sin ABC.
b) Vẽ đường cao BK. Tính BK và sin BAC.
1. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=4cm,AC=9cm. Tính sin B, sin C
2.Cho tam giác ABC vuông tại A, Cos B= an pha, Cos = 4/5. Tính sin, tan,cos
3. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=6cm, BC= 10cm
a. Tính AC,AH. Tỉ số đồng giác góc B,C
b. Gọi E,F lần lượt là hình chiếu H lên AB,AC. CM :AE.AD=AF.AC
c. Tính S tứ giác AEHF
Tính giá trị của biểu thức
A=sin^2sin70°+sin^2sin80°+sin^2sin10°+sin^2sin20°
2 cho tam giác ABC vuông tại C AB = 10cm AC = 8cm . Gọi CH là đường cao và CD là đường giác trong của góc C ( D thuộc AB)
A/ giải tam giác vuông
B/ tính độ dài của đường cao CH
C/ tính diện tích của BDC
Cho tam giác ABC vuông tại A có AB = c, AC = b, đường phân giác trong AD = d. Gọi E, F là hình chiếu của D trên AB và AC
a) Tính chu vi và diện tích tứ giác AEDF
b) Chứng minh: (√2) / d = 1 / b + 1 / c
c) Chứng minh: 1/ sin (A/2) + 1 / sin (B/2) + 1 / sin (C/2) > 6
Cho tam giác ABC vuông tại A có AC= 4cm, AB+BC= 8cm. Tính sin B, sin C, tan \(\frac{B}{2}\)
BÀI 1 :cho tam giác ABC vuông tại A có AB=4cm BC=6cm. tính tỉ số lượng giác của các góc B và C
BÀI 2 :đơn giản các biểu thức
a)\(A=\cos^2x+\cos^2x.\cot g^2x\)
b)\(sin^2x+\sin^2x.\tan^2x\)
c)\(\dfrac{2cos^2x-1}{\sin x+\cos x}\)
d)\(\dfrac{\cos x}{1+\sin x}+\tan x\)
Cho tam giác ABC nhọn có BC=a, AC=b, AB=c
Chứng minh
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)