Cho🔺️ABC cân tại A (góc A
TV
Những câu hỏi liên quan
Cho🔺️ABC cân tại A (góc A
Cho🔺️ABC cân tại A. Trên tia đối của tia BC lấy điểm D ,trên tia đối của tia CB lấy điểm E sao cho BD=CE. Kẻ BH vuông góc với AD tại H ,CK vuông góc với AE tại K .Chứng minh : a) 🔺️BHD=🔺️CKE . b) 🔺️ABH=🔺️AKC . c) BC // HK .
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\) và AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
c: Xét ΔADE có AH/AD=AK/AE
DO đó: HK//DE
hay BC//HK
Đúng 1
Bình luận (0)
Giải giúp gấp với ạ💦💦 . . . Cho 🔺️ABC cân tại A, có ABM = 50° và AM là đường cao. a) CM 🔺️ABM = 🔺️ACM. b) So sánh MA và MB c)Đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AC tại C cắt nhau tại I. Chứng minh: A, M, I thẳng hàng
a: Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
=>ΔABM=ΔACM
b: góc MAB=90-50=40 độ<góc ABM
=>MB<MA
c: Xét ΔABI vuông tại B và ΔACI vuông tại C có
AI chung
AB=AC
=>ΔABI=ΔACI
=>IB=IC
=>I nằm trên trung trực của BC
mà AM là trung trực của BC
nên A,M,I thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC CÓ AB=AC .KẺ BH VUÔNG GÓC VỚI AC TẠI H VÀ CK VUÔNG GÓC VỚI AB TẠI K . GỌI O LÀ GIAO ĐIỂM của BH và CK . Biết CH=BK ,chứng minh a)🔺️ABI=🔺️ACI B)🔺️AIH= 🔺️AIK C)🔺️BIH=🔺️CIK
Sửa đề: I là giao của BH và CK
a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KB=HC
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
AH=AK
=>ΔAHI=ΔAKI
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia tia AB lấy điểm D. Trên tia đối của tia AC lấy điểm E sao cho AD = AE. Chứng minh: a) DE // BC b) BE = CD c) 🔺️BED = 🔺️CDE.
tham khảo
a) Vì tam giác ABc cân nên :
góc B = góc C
Lại vì AE=Ad => tam giác AED cần
=> Góc E = góc D
Ta có:
góc E + góc D+ góc EAD = Góc B + góc C+ góc BAC(=180 độ)
mà góc EAD = góc BAC ( đói đỉnh)
=> góc E + góc D = góc B+ góc C
mặt khác :góc B = góc C , Góc E = góc D
=> Góc E= góc C mà 2 góc này ơ vị trí so le trong nên :ED// BC ( đpcm)
Đúng 0
Bình luận (0)
\(\text{Hình bạn tự vẽ nhoa!}\)
\(\text{a)}\Delta ABC\text{ cân tại }A:\)
\(\Rightarrow\widehat{B}=\widehat{C}\)
\(\text{Vì }AD=AE\)
\(\Rightarrow\Delta AED\text{ cân tại A}:\)
\(\Rightarrow\widehat{E}=\widehat{D}\)
\(\text{Ta có:}\widehat{B}+\widehat{C}+\widehat{BAC}=\widehat{E}+\widehat{D}+\widehat{EAD}=180^0\)
\(\text{mà }\widehat{EAD}\text{ và }\widehat{BAC}\text{(đối đỉnh)}\)
\(\Rightarrow\widehat{E}+\widehat{D}=\widehat{B}+\widehat{C}\)
\(\Rightarrow\widehat{E}=\widehat{C}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow ED=BC\)
\(\text{b)Xét }\Delta EAB\text{ và }\Delta DAC\text{ có:}\)
\(AE=AD\left(gt\right)\)
\(AB=AC\left(cmt\right)\)
\(\widehat{EAB}=\widehat{CAD}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta EAB=\Delta DAC\left(c.g.c\right)\)
\(BE=CD\text{(2 cạnh tương ứng)}\)
\(\text{c)Ta có:}\Delta EAB=\Delta DAC\left(cmt\right)\)
\(\Rightarrow\widehat{AEB}=\widehat{ADC}\)
\(\text{mà }\widehat{AED}=\widehat{ADE}\)
\(\Rightarrow\widehat{AEB}+\widehat{AED}=\widehat{ADC}+\widehat{ADE}\)
\(\text{Xét }\Delta BED\text{ và }\Delta CDE\text{ có:}\)
\(BE=CD\left(cmt\right)\)
\(\widehat{BED}=\widehat{CDE}\left(cmt\right)\)
\(ED\text{ chung}\)
\(\Rightarrow\Delta BED=\Delta CDE\left(c.g.c\right)\)
Đúng 3
Bình luận (7)
Cho 🔺️ABC vuông tại A. Đg cao AH(H thuộc BC) cắt tia phân giác BD của góc ABC tại I. CMR:
a) IA. BH= IH. AB
b) AB2= BH. BC
1.Cho 🔺️EMN cân tại E ( Ê < 90° ) , các đường cao MA, NB cắt nhau tại I . Tia EI cắt MN tại H.
a, CM : 🔺️AMN = 🔺️BNM
b, CM : EH là đường trung tuyến của 🔺️EMN
c, Tính độ dài đoạn thẳng MA biết AE= 3cm , AN= 2cm . ( Sử dụng định lí Py-ta-go )
d, CM : I cách đều 3 cạnh của 🔺️ABH
Bài Làm
a) Xét tam giác AMN và tam giác BNM có:
\(\widehat{A}=\widehat{B}\)(=90o)
MN chung
\(\widehat{M}=\widehat{N}\)(vì tam giác AMN cân tại E)
=> tam giác AMN=tam giác BNM( ch-gn)
b) Ta có \(MA\perp EN\)
\(NB\perp EM\)
Mà MA cắt NB tại I => I là trực tâm của tam giác EMN
=> \(EH\perp MN\)
Vậy EH là đường trung tuyến của tam giác EMN
c) Ta có EA+AN=EN
hay 2 + 3 = EN
2 + 3 = 5 (cm)
VÌ tam giác EMN cân tại E nên : EM=EN=5 cm
Xét tam giác EMA có:
ME2 = MA2 + EA2
52 = MA2 + 22
MA2 = 52 -22
MA2 = 25-4
MA2 = 21
\(MA=\sqrt{21}\)
( MÌNH CHỈ BIẾT LÀM ĐẾN ĐÂY THÔI,MONG BẠN THÔNG CẢM MK HƠI KO ĐC THÔNG MINH! HÌNH BẠN TỰ VẼ NHÉ)
CHÚC BẠN HỌC TỐT!!!!!!!!^_^
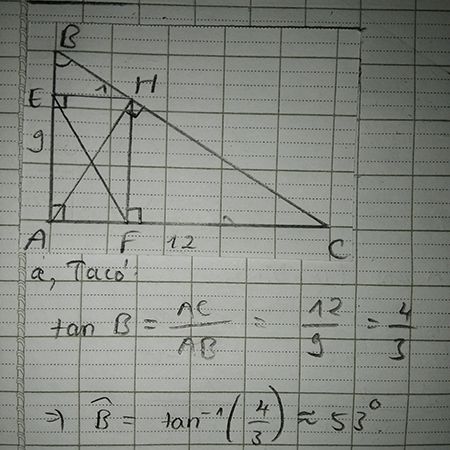
Cho 🔺️ABC vuông tại A. Đường cao AH. Biết AB =9cm , AC =12cm a) tính độ dài BC ,AH và số đo góc C ( làm tròn đến phút ) b) phân giác của góc BAC cắt BC tại D . Tính độ dài BD Mn giúp ien với ạ
Cho 🔺️ABC có BC =2AB . Gọi M là trung điểm của BC, D là trung điểm của BM. Trên tia đối của DAClaasy E sao cho DE=DA.Gọi I là giao điểm của AC và EM
a) CM ABEI là hình thang
b)cm 🔺️AME=🔺️MAC
c) CEDI là hình thang cân
a, \(\Delta ADB=\Delta EDM\left(c.g.c\right)\Rightarrow\widehat{BAD}=\widehat{MED}\) ( 2 góc tương ứng )
\(\Rightarrow AB//EI\)( vì co 2 góc so le trong bằng nhau )
\(\Rightarrow ABEI\)là hình thang
b, \(AB=ME=\frac{1}{2}BC\)
M là trung điểm của BC (gt) nên \(MB=MC=\frac{1}{2}BC\)
\(\Rightarrow AB=MB=MC=ME\)
\(\Rightarrow\Delta AMB\)cân tại B \(\Rightarrow\widehat{BAM}=\widehat{AMD}\) (t/c)
\(AB//EI\left(gt\right)\Rightarrow\widehat{BAM}=\widehat{AMI}\)(SLT)
Ta có: \(\hept{\begin{cases}\widehat{DME}=\widehat{IMC}\\\widehat{AMD}=\widehat{AMI}\left(cmt\right)\end{cases}}\)
\(\Rightarrow\widehat{AME}=\widehat{AMC}\)
\(\Delta AME=\Delta AMC\left(c.g.c\right)\)\(\Rightarrow AE=AC\)( 2 cạnh t/ứ)
c, \(\Delta AEC\)cân tại A \(\Rightarrow\widehat{AEC}=\widehat{ACE}\) hay \(\widehat{DEC}=\widehat{ICE}\) (1)
\(\Delta ABC\)có: M là trung điểm của BC và MI // AB nên I là trung điểm của AC
DI là đường trung bình của \(\Delta AEC\Rightarrow DI//EC\) (2)
Từ (1) và (2) \(\Rightarrow CEDI\)là hình thang cân.
Chúc bạn học tốt.
Đúng 0
Bình luận (0)