Cho tam giác ABC có hai đường cao A,A1 . B,B1 . CMR A1B1C ĐỒNG DẠNG ABC
TP
Những câu hỏi liên quan
Cho tam giác ABC, các đường cao BD, CE. CMR:
a. Tam giác ABD đồng dạng vs tam giác ACE.
b. Tam giác ADE đồng dạng vs tam giác ABC.
a, Xét tam giác ABD và tam giác ACE
+, Chung góc A
+, Góc ADB = góc AEC( = 90 độ)
Suy ra tam giác ABD đồng dạng với tam giác ACE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại H có AH là đường cao (H thuộc BC) a) CMR tam giác ABC đồng dạng tam giác HAC b) Tính HC.BC=BC^2-AB^2
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
b: ΔABC đồng dạng với ΔHAC
=>CA/CH=CB/CA
=>CH*CB=CA^2=BC^2-AB^2
Đúng 0
Bình luận (0)
cho tam giác abc có 3 góc nhọn, hai đường cao BE, CF, AH cắt nhau tại H: a)AE.AC=AF.AB . b) CMR: Tam giác(tg)AEF~tgABC. c)CMR: tam giác AEF đồng dạng tam giác CED từ đó suy ra: Tia EH là phân giác góc FED
a: Xét ΔAEB vuông ạti E và ΔAFC vuôg tại F có
góc BAE chung
=>ΔAEB đồng dạg vơi ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng vơi ΔABC
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a, đường cao ah đường trung tuyến am
a) cmr tam giác abc đồng dạng tam giác hba
b) ah^2=bh.ch
Xét tam giác ABC và HBA có góc A = góc H =90 độ & góc B chung . => tam giác ABC đồng dạng tam giác HBA (G-G)Xét tam giác AHB và tam giác CHA có AHB =CHA =90 độ & góc HAB = HCA ( cùng phụ góc B) Suy ra tam giác AHB đồng dạng CHA (g-g). Suy ra AH/CH =BH/AH hay AB2=BH.CH
Đúng 0
Bình luận (0)
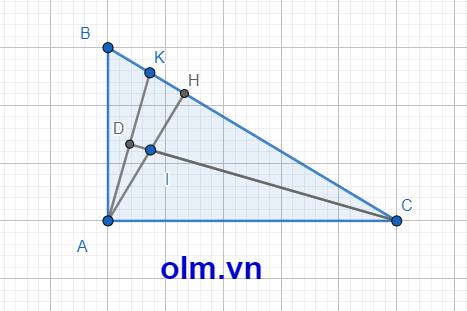
cho tam giác abc vuông tại a đường cao ah gọi i, k lần lượt là trung điểm của hai cạnh ah và bh.
a) cmr: tam giác ahk đồng dạng với tam giác chi
b) CMR: ak vuông góc với ci
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC có ba đường cao AD, BE, CFcắt nhau tại H. CMR
a, tam giác AEB đồng dạng tam giác AFC
b, tam giác ABC đồng dạng tam giác AEF
c, HD/AD + HE/BE + HF/CF =1
Giúp mk vs !
a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)
b) Ta có: ΔAEB∼ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔAEF∼ΔABC(c-g-c)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhon nội tiếp đường tròn O. Ba đường cao AD, BE, CF cắt nhau tại H
a) Cmr: Tứ giác AEHF nội tiếp
b) Cmr: Tứ giác BCEF nội tiếp
c) Cmr: Tam giác AEB đồng dạng tam giác AFC
d) Cmr: Tam giác AEF đồng dạng tam giác ABC
Cho tam giác ABC có 3 góc nhọn , các đường cao BD và CE cắt nhau tại H
a. CMR: tam giác ABD đồng dạng với tam giác ACE
b. CMR: HB.HD=HC.HE
c.Cm: GÓC ADE= GÓC ABC
vẽ hình
a xét tam giác ABD và tam giác ACE có :
chung góc BAC
góc BDA = góc CEA = 90 độ
=> tam giác ABD đồng dạng tam giác ACE (g.g)
b, xét tam giác EHB và tam giác DHC có
góc BDC = góc CFB = 90 độ
góc BHF = góc DHC ( đối đỉnh )
=> tam giác EHB đồng dạng với tam giác DHC (g.g)
=> \(\frac{HB}{HC}=\frac{HE}{HD}\)
=> HD . HB = HE . HC ( đpcm )
c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\) => \(\frac{AE}{AC}=\frac{AD}{AB}\)
xét tam giác ADE và tam giác ABC có
chung góc BAC
\(\frac{AE}{AC}=\frac{AD}{AB}\)
=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
=> góc ADE = góc ABC ( đpcm)
Đúng 0
Bình luận (0)
Trên các cạnh BC, CA, AB của tam giác ABC tương ứng lấy các điểm A1, B1, C1. Gọi Ga, Gb, Gc theo thứ tự là trọng tâm các tam giác AB1C1, C1A1B, A1B1C và G, G1, G2 là trọng tâm của các tam giác ABC, A1B1C1, GaGbGc theo thứ tự đó. Chứng minh rằng G, G1, G2 thẳng hàng.
Từ giả thiết suy ra với mọi O đều có ?
\(\overrightarrow{OG}=\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\) và \(\overrightarrow{OG_1}=\frac{1}{3}\left(\overrightarrow{OA}_1+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\)
Mà :
\(\overrightarrow{OG_2=}\frac{1}{3}.\left(\overrightarrow{OGa}+\overrightarrow{OG_b}+\overrightarrow{OG_c}\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB_1}+\overrightarrow{OC_1}\right)+\frac{1}{3}\left(\overrightarrow{OB}+\overrightarrow{OC_1}+\overrightarrow{OA_1}\right)+\frac{1}{3}\left(\overrightarrow{OC}+\overrightarrow{OA_1}+\overrightarrow{OB_1}\right)\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\frac{2}{3}\left(\overrightarrow{OA_1}+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\right)\)
\(=\frac{1}{3}\overrightarrow{OG}+\frac{2}{3}\overrightarrow{OG_1}\)
Suy ra :
\(3\overrightarrow{OG_2}=\overrightarrow{OG}+2\overrightarrow{OG_1}\) với mọi O. Điều này có nghĩa là \(G,G_1,G_2\) thẳng hàng => Điều phải chứng minh
Đúng 0
Bình luận (0)




