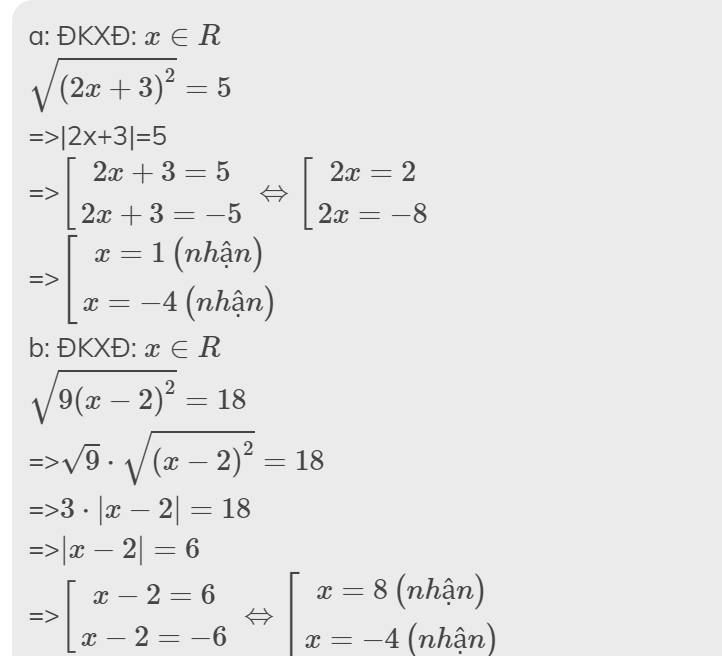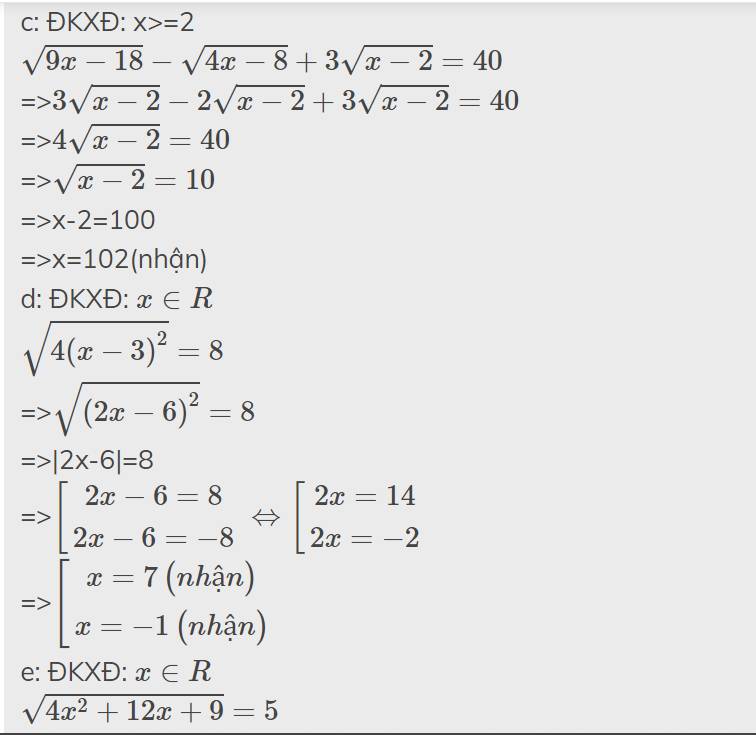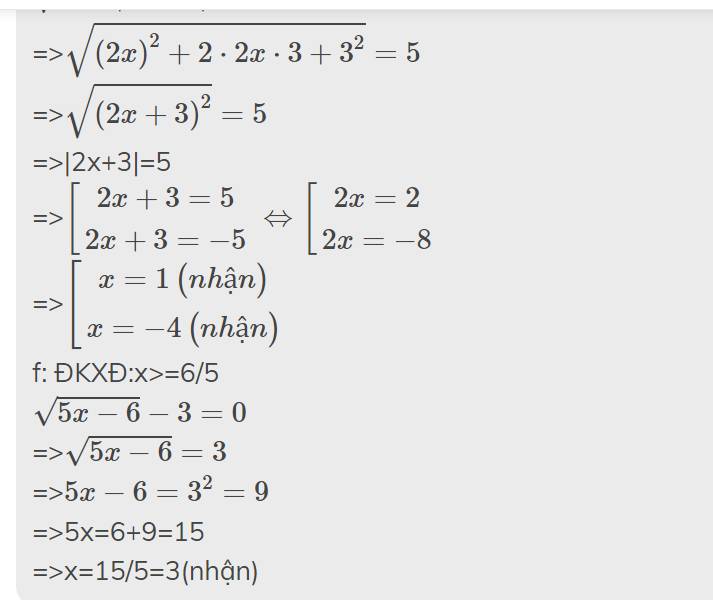\(x\sqrt{18}-\sqrt{18}=x\sqrt{18}+4\sqrt{2}\)
HD
Những câu hỏi liên quan
\(x\sqrt{18}-\sqrt{18}=x\sqrt{8}+4\sqrt{2}\)
x√18 - √18 = x√8 + 4√2
3x√2 - 3√2 = 2x√2 + 4√2
3x√2 - 2x√2 = 4√2 + 3√2
x√2 = 7√2
x = 7
Đúng 1
Bình luận (0)
\(x\sqrt{18}-\sqrt{18}=x\sqrt{8}+4\sqrt{2}\\\Leftrightarrow x\sqrt{18}-\sqrt{18}=2\sqrt{2}x+4\sqrt{2}\\ \Leftrightarrow\sqrt{18}\left(x-1\right)=2\sqrt{2}\left(x+2\right)\\ \Leftrightarrow3\sqrt{2}\left(x-1\right)=2\sqrt{2}\left(x+2\right)\\ \Leftrightarrow3x-3=2x+4\\ \Leftrightarrow x=7\)
Vậy x = 7
Đúng 1
Bình luận (0)
1. Đưa các căn bậc hai về dạng tối giản: x√18 - √18 = x√8 + 4√2 √18 (x - 1) = √8 (x + 4√2) 2. Bình phương cả hai vế của phương trình: 18(x - 1)² = 8(x + 4√2)² 18(x² - 2x + 1) = 8(x² + 8√2x + 32) 3. Mở ngoặc và thu gọn các thành phần tương ứng: 18x² - 36x + 18 = 8x² + 64√2x + 256 4. Đưa tất cả các thành phần về một vế và đưa các hạng tử cùng cấp về cùng một vế: 18x² - 8x² - 36x - 64√2x + 18 - 256 = 0 10x² - 100√2x - 238 = 0 5. Giải phương trình bậc hai: Áp dụng công thức giải phương trình bậc hai, ta có: x = (-b ± √(b² - 4ac)) / (2a) Ứng với phương trình 10x² - 100√2x - 238 = 0, ta có: a = 10, b = -100√2, c = -238 x = (-(-100√2) ± √((-100√2)² - 4(10)(-238))) / (2(10)) x = (100√2 ± √(20000 + 9520)) / 20 x = (100√2 ± √29520) / 20 6. Tính toán giá trị x bằng cách tính căn bậc hai: x = (100√2 ± √(4 × 7380)) / 20 x = (100√2 ± √(4 × 2 × 3690)) / 20 x = (100√2 ± √(4 × 2 × 2 × 1845)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 615)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 205)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√2 ± √(4 × 2 × 2 × 3 × 3 × 5 × 41)) / 20 x = (100√Để giải phương trình x√18 - √18 = x√8 + 4√2, ta có thể thực hiện các bước sau: 1. Nhân cả hai vế của phương trình với √18 để loại bỏ căn bậc hai trong phương trình: (x√18 - √18)√18 = (x√8 + 4√2)√18 x√18√18 - √18√18 = x√8√18 + 4√2√18 18x - 18 = 18x√8 + 72√2 2. Tiếp theo, chúng ta có thể nhóm các thành phần có x trong phương trình: 18x - 18 - 18x√8 = 72√2 -18 - 18x√8 = 72√2 - 18x 3. Tiếp theo, chúng ta có thể chia cả hai vế của phương trình cho -18 để đơn giản hóa: 1 + x√8 = -4√2 + x 4. Tiếp theo, chúng ta có thể di chuyển các thành phần có x về cùng một vế của phương trình: x - x√8 = -4√2 - 1 5. Tiếp theo, chúng ta có thể nhân cả hai vế của phương trình với √8 để loại bỏ căn bậc hai trong phương trình: x√8 - x√8√8 = -4√2√8 - √8 8x - 8 = -4√16 - √8 8x - 8 = -4(4) - √8 8x - 8 = -16 - √8 6. Tiếp theo, chúng ta có thể di chuyển các thành phần không có x về cùng một vế của phương trình: 8x + √8 = -16 - 8 7. Tiếp theo, chúng ta có thể đơn giản hóa phương trình: 8x + √8 = -24 8. Cuối cùng, chúng ta có thể giải phương trình để tìm giá trị của x: 8x = -24 - √8 x = (-24 - √8)/8 Vậy giá trị của x là (-24 - √8)/8....
Đúng 0
Bình luận (0)
rút gọn biểu thức sau
D=\(\left(\sqrt{x-\sqrt{18}}-\sqrt{x+\sqrt{18}}\right)\sqrt{x+\sqrt{x^2-18}}\) với \(x\ge18\)
A=\(\sqrt{x+6\sqrt{x-9}}+\sqrt{x-6\sqrt{x-9}}\)
C=\(\dfrac{\sqrt{2-\sqrt{2-4-x^2}}\left[\sqrt{\left(2+x\right)^3}+\sqrt{\left(2-x\right)^3}\right]}{4-\sqrt{4-x^2}}\)
a)\(\sqrt{4x-12}+\sqrt{9x-27}-4\sqrt{x-3}+3-x\)
b) \(\sqrt{25x-25}-3\sqrt{x-2}=2+4\sqrt{x+3}+\sqrt{9x-18}\)
c) \(\sqrt{49x-98}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+18\)
d) \(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=\sqrt{2}\)
giúp mk vs
a: \(=2\sqrt{x-3}+3\sqrt{x-3}-4\sqrt{x-3}+3-x\)
\(=\sqrt{x-3}+3-x\)
c: \(\Leftrightarrow7\sqrt{x-2}-2\sqrt{x-2}-3\sqrt{x-2}=18\)
=>2 căn x-2=18
=>x-2=81
=>x=83
Đúng 0
Bình luận (0)
GIẢI PHƯƠNG TRÌNH
a) \(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\)
b) \(\sqrt{9x^2+12x+4}=4x\)
c) \(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
d) \(\sqrt{5x-6}-3=0\)
a: \(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\cdot3\sqrt{x-2}+6\cdot\dfrac{\sqrt{x-2}}{9}=-4\)
\(\Leftrightarrow\sqrt{x-2}=4\)
=>x-2=16
hay x=18
b: \(\Leftrightarrow\left|3x+2\right|=4x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=4x\left(x>=-\dfrac{2}{3}\right)\\3x+2=-4x\left(x< -\dfrac{2}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-\dfrac{2}{7}\left(nhận\right)\end{matrix}\right.\)
c: \(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
\(\Leftrightarrow4\sqrt{x-2}=40\)
=>x-2=100
hay x=102
d: =>5x-6=9
hay x=3
Đúng 1
Bình luận (0)
\(a,\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\left(dk:x\ge2\right)\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\left(tmdk\right)\)
b,\(\sqrt{9x^2-12x+4=3x\left(dk:x\ge0\right)}\)
\(\Leftrightarrow\sqrt{\left(3x-2\right)^2}=3x\)
\(\Leftrightarrow\left|3x-2\right|=3x\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-2=3x\\3x-2=-3x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\in\varnothing\\x=\dfrac{1}{3}\left(tmdk\right)\end{matrix}\right.\)
Các câu còn lại làm tương tự nhé
Đúng 0
Bình luận (0)
\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: x≥2)
\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+6\sqrt{\dfrac{1}{81}\left(x-2\right)}=-4\)
\(\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{4}{3}\sqrt{x-2}=-4\)
\(-\sqrt{x-2}=-4\)
\(\sqrt{x-2}=4\)
\(\left|x-2\right|=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=16\\x-2=-16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=18\left(TM\right)\\x=-14\left(L\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9.\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{4x^2+12x+9}=5\)
\(\sqrt{5x-6}-3=0\)
a: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(2x+3\right)^2}=5\)
=>|2x+3|=5
=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
b: ĐKXĐ: \(x\in R\)
\(\sqrt{9\left(x-2\right)^2}=18\)
=>\(\sqrt{9}\cdot\sqrt{\left(x-2\right)^2}=18\)
=>\(3\cdot\left|x-2\right|=18\)
=>\(\left|x-2\right|=6\)
=>\(\left[{}\begin{matrix}x-2=6\\x-2=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: x>=2
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
=>\(3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
=>\(4\sqrt{x-2}=40\)
=>\(\sqrt{x-2}=10\)
=>x-2=100
=>x=102(nhận)
d: ĐKXĐ: \(x\in R\)
\(\sqrt{4\left(x-3\right)^2}=8\)
=>\(\sqrt{\left(2x-6\right)^2}=8\)
=>|2x-6|=8
=>\(\left[{}\begin{matrix}2x-6=8\\2x-6=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=14\\2x=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2+12x+9}=5\)
=>\(\sqrt{\left(2x\right)^2+2\cdot2x\cdot3+3^2}=5\)
=>\(\sqrt{\left(2x+3\right)^2}=5\)
=>|2x+3|=5
=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
f: ĐKXĐ:x>=6/5
\(\sqrt{5x-6}-3=0\)
=>\(\sqrt{5x-6}=3\)
=>\(5x-6=3^2=9\)
=>5x=6+9=15
=>x=15/5=3(nhận)
Đúng 2
Bình luận (0)
Giải Phương Trình
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{5x-6}-3=0\)
Giải các phương trình sau:
a. \(\sqrt{25x+75}+3\sqrt{x-2}=2\sqrt{x-2}+\sqrt{9x-18}\)
b. \(\sqrt{\left(2x-1\right)^2}=4\)
c. \(\sqrt{\left(2x+1\right)^2}=3x-5\)
d. \(\sqrt{4x-12}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+8\)
a) Ta có: \(\sqrt{25x+75}+3\sqrt{x-2}=2\sqrt{x-2}+\sqrt{9x-18}\)
\(\Leftrightarrow5\sqrt{x+3}+3\sqrt{x-2}=2\sqrt{x-2}+3\sqrt{x-2}\)
\(\Leftrightarrow\sqrt{25x+75}=\sqrt{4x-8}\)
\(\Leftrightarrow25x-4x=-8-75\)
\(\Leftrightarrow21x=-83\)
hay \(x=-\dfrac{83}{21}\)
b) Ta có: \(\sqrt{\left(2x-1\right)^2}=4\)
\(\Leftrightarrow\left|2x-1\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
c) Ta có: \(\sqrt{\left(2x+1\right)^2}=3x-5\)
\(\Leftrightarrow\left|2x+1\right|=3x-5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=3x-5\left(x\ge-\dfrac{1}{2}\right)\\2x+1=5-3x\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3x=-5-1\\2x+3x=5-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\left(nhận\right)\\x=\dfrac{4}{5}\left(loại\right)\end{matrix}\right.\)
d) Ta có: \(\sqrt{4x-12}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+8\)
\(\Leftrightarrow2\sqrt{x-3}-2\sqrt{x-2}=3\sqrt{x-2}+8\)
\(\Leftrightarrow2\sqrt{x-3}-5\sqrt{x-2}=8\)
\(\Leftrightarrow4\left(x-3\right)+25\left(x-2\right)-20\sqrt{x^2-5x+6}=8\)
\(\Leftrightarrow4x-12+25x-50-8=20\sqrt{\left(x-2\right)\left(x-3\right)}\)
\(\Leftrightarrow20\sqrt{\left(x-2\right)\left(x-3\right)}=29x-70\)
\(\Leftrightarrow x^2-5x+6=\dfrac{\left(29x-70\right)^2}{400}\)
\(\Leftrightarrow x^2-5x+6=\dfrac{841}{400}x^2-\dfrac{203}{20}x+\dfrac{49}{4}\)
\(\Leftrightarrow\dfrac{-441}{400}x^2+\dfrac{103}{20}x-\dfrac{25}{4}=0\)
\(\Delta=\left(\dfrac{103}{20}\right)^2-4\cdot\dfrac{-441}{400}\cdot\dfrac{-25}{4}=-\dfrac{26}{25}\)(Vô lý)
vậy: Phương trình vô nghiệm
Đúng 0
Bình luận (0)
Cho A = \(\frac{2x+15\sqrt{x}+18}{x+3\sqrt{x}-18}+\frac{3x+4\sqrt{x}+1}{2x-3\sqrt{x}-5}-\frac{8x-15\sqrt{x}}{2x\sqrt{x}-11x+5\sqrt{x}}\)
Tính A tại \(x=\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\)
Tìm x:
\(\sqrt{x^2-6x+10}+\sqrt{x^2-6x+18}+\sqrt{x^2-6x+12}=4+\sqrt{3}\)