số đối của x+3 +số đối của 2y-6 =0
NH
Những câu hỏi liên quan
Tọa độ cặp điểm thuộc đồ thị (C) của hàm số y
x
+
4
x
-
2
đối xứng nhau qua đường thẳng d: x-2y-6 0 là A. B. C. D.
Đọc tiếp
Tọa độ cặp điểm thuộc đồ thị (C) của hàm số y = x + 4 x - 2 đối xứng nhau qua đường thẳng d: x-2y-6 = 0 là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án B

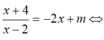
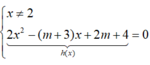
Điều kiện cần:
Để ∆ cắt (C) tại hai điểm phân biệt thì phương trình h(x) = 0 có hai nghiệm phân biệt khác 2, tức là
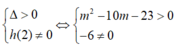
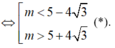
Điều kiện đủ:
Gọi I là trung điểm của AB, ta có:
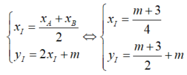
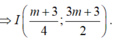

![]()
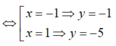
Vậy tọa hai điểm cần tìm là
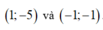
Đúng 0
Bình luận (0)
1 .
a ) ( x -1 ) . ( 2y + 2 ) = 8
b ) Trị tuyệt đối của x - 2 + trị truyệt đối của 2y -4 = 0
a, \(\left(x+1\right)\left(2y+2\right)=8\)
\(\Leftrightarrow x+1;2y+2\inƯ\left(8\right)\)
Tự xét tiếp nhé!
b, \(\left|x-2\right|+\left|2y-4\right|=0\)
Mà \(\hept{\begin{cases}\left|x-2\right|\ge0\\\left|2y-4\right|\ge0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left|x-2\right|=0\\\left|2y-4\right|=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\y=2\end{cases}}\)
Vậy ...
Đúng 0
Bình luận (0)
1. cho pt x2-2(m-2)x-2m0 với x là ẩn số giá trị của m để pt có 2 nghiệm là 2 số đối nhau là a,0 b, dfrac{-1}{2} c, 2 d, 4 2. biết rằng (x0; y0)là nghiệm của hệ pt left{{}begin{matrix}x+2y-302x-y-10end{matrix}right. tổng x0 + y0 bằng a,3 b,1 c,0 d, 23. trong △ABC vuông tại A có AC3; AB4 khi đó tanB bằng a,dfrac{4}{5} b,dfrac{3}{5} c,dfrac{3}{4} d dfrac{4}{3}4. trên đg tròn (O;R) lấy 2 điểm A,B sao cho số đo cung AB lớn hơn...
Đọc tiếp
1. cho pt x2-2(m-2)x-2m=0 với x là ẩn số giá trị của m để pt có 2 nghiệm là 2 số đối nhau là
a,0 b, \(\dfrac{-1}{2}\) c, 2 d, 4
2. biết rằng (x0; y0)là nghiệm của hệ pt \(\left\{{}\begin{matrix}x+2y-3=0\\2x-y-1=0\end{matrix}\right.\) tổng x0 + y0 bằng
a,3 b,1 c,0 d, 2
3. trong △ABC vuông tại A có AC=3; AB=4 khi đó tanB bằng
a,\(\dfrac{4}{5}\) b,\(\dfrac{3}{5}\) c,\(\dfrac{3}{4}\) d \(\dfrac{4}{3}\)
4. trên đg tròn (O;R) lấy 2 điểm A,B sao cho số đo cung AB lớn hơn bằng \(270^o\) độ dài dây cung là
a, R\(\sqrt{2}\) b, R\(\sqrt{3}\) c, R d, 2R\(\sqrt{2}\)
5. cho đg tròn (O;3cm) 2 điểm A,B thuộc đường tròn và sđ \(\stackrel\frown{AB}\) = \(60^o\) độ dài cung nhỏ AB là
a, \(\dfrac{\pi}{2}\) cm b, \(3\pi\) c, \(\dfrac{\pi}{3}cm\) d, \(\pi\)cm
6. giá trị của m để 2 đg thẳng (d): y=xm+6 và (d'): y=3x+2-m song song là
a, m=-2 b, m=-3 c, m=-4 d, m=1
7. cho hàm số bậc nhất y=ax+b có hệ số góc bằng -1 và tung độ góc bằng 3 giá trị của biểu thức a2+b bằng
a,2 b, 4 c, 9 d, 5
8. cho hệ pt \(\left\{{}\begin{matrix}3x+my=1\\nx+y=3\end{matrix}\right.\) với m,n là tham số biết rằng (x;y)=(1,1) là 1 nghiệm của hệ đã cho giá trị của m+n bằng
a, -1 b, 3 c, 1 d, 2
9.cho Parabol (P) có pt \(y=\dfrac{x^2}{4}\) vào đường thẳng (d): y=-2x-4
a, (P) cắt (d) tại 2 điểm phân biệt
b, (P) cắt (d) tại điểm duy nhất (-2;2)
c, (P) ko cắt (d)
d, (P) tiếp xúc với (d), tiếp điểm là (-4;4)
10. tất cả các giá trị của x để \(\sqrt{-2x+6}\) có nghĩa là
a, x≥3 b, x>3 c, x≤3 d, x<-3
Câu 3: C
Câu 4: A
Câu 5: C
Câu 6: m=3
Câu 7: B
Câu 8: D
Câu 9: D
Câu 10: C
Đúng 1
Bình luận (0)
tìm các cặp số (x,y) thỏa mãn 2y^2=3- trị tuyệt đối của x+4
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: ( α 2 ): x − 2y + z + 3 = 0, ( α ' 2 ): x − 2y – z + 3 = 0
Xét vị trí tương đối của đường thẳng d: x + 2y – 2 = 0 với mỗi đường thẳng sau:
\({\Delta _1}{\rm{: }}3x{\rm{ }}--{\rm{ }}2y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\); \({\Delta _2}:{\rm{ }}x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0\); \({\Delta _3}:{\rm{ }}2x{\rm{ }} + {\rm{ }}4y{\rm{ }}--{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Xét hệ phương trình gồm phương trình của d và \({\Delta _1}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\3x - 2y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = \frac{3}{2}\end{array} \right.\)
Vậy d và \({\Delta _1}\) cắt nhau tại 1 điểm duy nhất.
Xét hệ phương trình gồm phương trình của d và \({\Delta _2}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\x + 2y + 2 = 0\end{array} \right.\). Hệ phương trình vô nghiệm.
Vậy d và \({\Delta _2}\) song song với nhau
Xét hệ phương trình gồm phương trình của d và \({\Delta _3}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\2x + 4y--4{\rm{ }} = {\rm{ }}0\end{array} \right.\). Hệ phương trình vô số nghiệm.
Vậy d và \({\Delta _3}\) trùng nhau.
Đúng 0
Bình luận (0)
Xét vị trí tương đối của hai đường thẳng
d
1
:
3
x
−
2
y
−
6
0
và
d
2
:
6
x
−
2
y
−
8
0
A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Đọc tiếp
Xét vị trí tương đối của hai đường thẳng d 1 : 3 x − 2 y − 6 = 0 và d 2 : 6 x − 2 y − 8 = 0
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Tìm số đối của +2; +3; - 6; 0; -1
Xét vị trí tương đối của mỗi cặp đường thẳng sau
a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\) ;
b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + 10 = 0\) ;
c) \({d_5}:4x + 2y - 3 = 0\) và \({d_6}:\left\{ \begin{array}{l}x = - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.\)
a) Tọa độ giao điểm của hai đường thẳng \({d_1},{d_2}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}3x + 2y - 5 = 0\\x - 4y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{9}{7}\\y = \frac{4}{7}\end{array} \right.\)
Hệ phương trình có nghiệm duy nhất nên 2 đường thẳng cắt nhau.
b) Tọa độ giao điểm của hai đường thẳng \({d_3},{d_4}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 2y + 3 = 0\\ - 2x + 4y + 10 = 0\end{array} \right.\) .
Hệ phương trình vô nghiệm.nên 2 đường thẳng song song với nhau
c) Tọa độ giao điểm của hai đường thẳng \({d_5},{d_6}\) tương ứng với t thỏa mãn phương trình:
\(4\left( { - \frac{1}{2} + t} \right) + 2\left( {\frac{5}{2} - 2t} \right) - 3 = 0 \Leftrightarrow 0t = 0\) .
Phương trình này có nghiệm với mọi t. Do đó \({d_5} \equiv {d_6}\).
Đúng 0
Bình luận (0)



