Giúp em ( bài 1 câu d )với ạ
HG
Những câu hỏi liên quan
giúp em bài 1 câu c câu d với ạ!!!

`D=(sqrt{3}.sqrt{5-2sqrt6})/(sqrt3-sqrt2)-1/(2-sqrt3)`
`=(sqrt3*sqrt{3-2sqrt{3}.sqrt2+2})/(sqrt3-sqrt2)-(2+sqrt3)/(4-3)`
`=(sqrt3.sqrt{(sqrt3-sqrt2)^2})/(sqrt3-sqrt2)-2-sqrt3`
`=sqrt3-2-sqrt3=-2`
Đúng 1
Bình luận (3)
c) Ta có: \(C=\sqrt{\dfrac{3\sqrt{5}+1}{2\sqrt{5}-3}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{\left(3\sqrt{5}+1\right)\left(2\sqrt{5}-3\right)}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{30-9\sqrt{5}+2\sqrt{5}-3}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{27-7\sqrt{5}}}{2\sqrt{5}-3}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{54-14\sqrt{5}}}{2\sqrt{10}-3\sqrt{2}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\dfrac{\left(7-\sqrt{5}\right)\cdot\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{2}\cdot\left(2\sqrt{5}-3\right)}\)
\(=\dfrac{7\sqrt{5}-7-5+\sqrt{5}}{2\sqrt{5}-3}\)
\(=\dfrac{8\sqrt{5}-12}{2\sqrt{5}-3}\)
\(=\dfrac{4\left(2\sqrt{5}-3\right)}{2\sqrt{5}-3}=4\)
Đúng 0
Bình luận (0)
Làm giúp em bài 1 câu (c) và câu (d) với ạ 
Moị người giúp em bài 1 câu d,e,f với ạ
Mọi người giúp em câu c bài 3 với câu c,d bài 4 với ạ 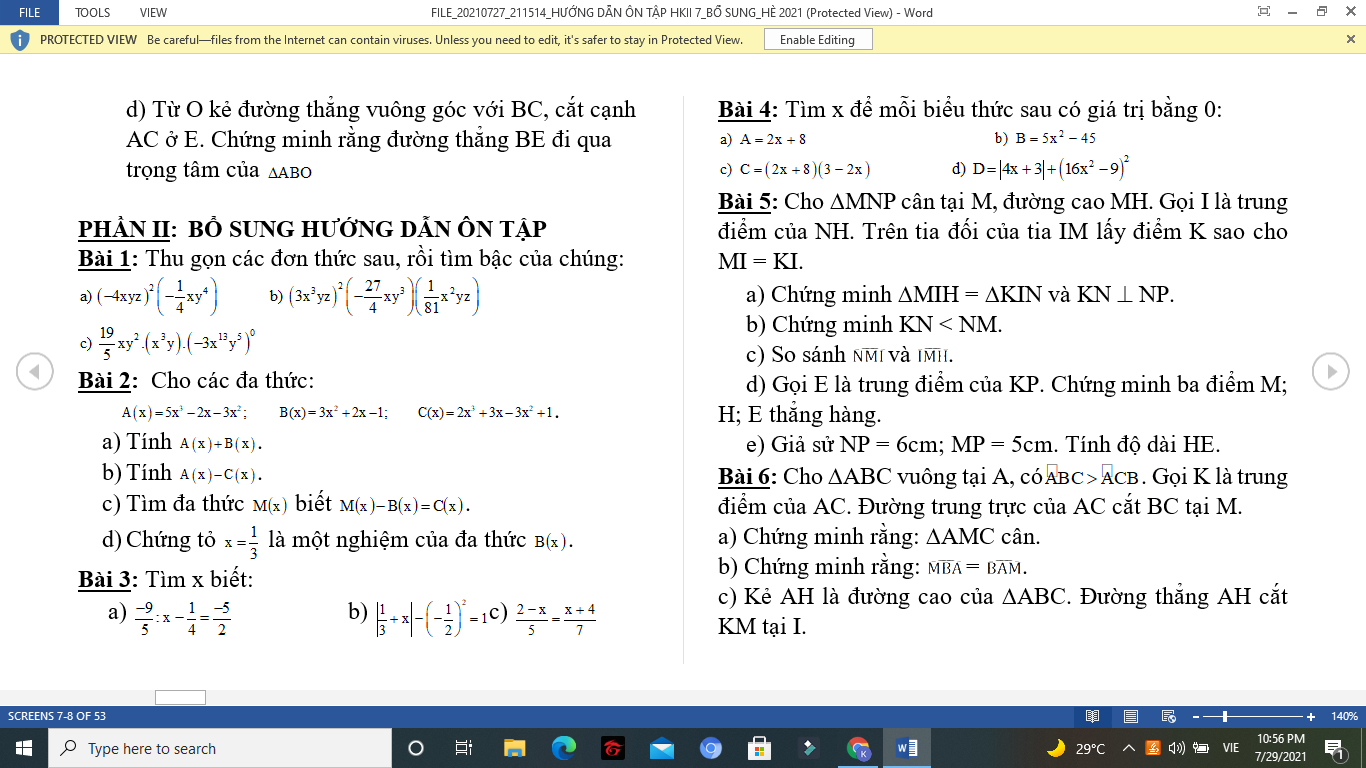
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
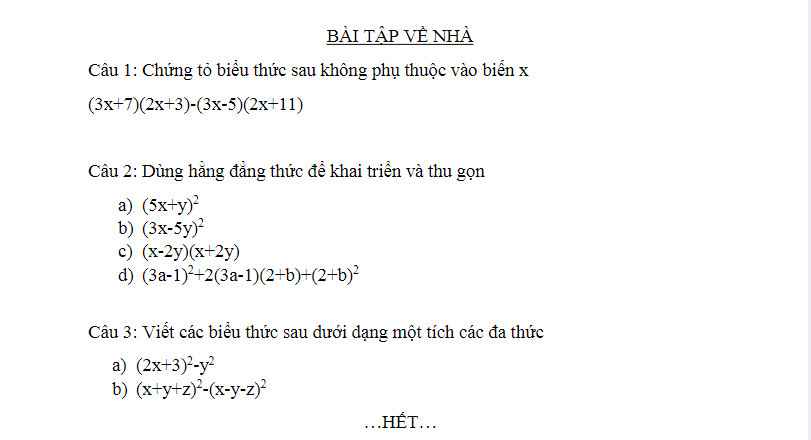
Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76
Đúng 1
Bình luận (2)
Mọi người giúp em câu 1 với mở bài câu 2 với ạ. Em cảm ơn trước ạ!

Giúp em câu 3c,d để mai em còn nộp bài với ạ
GIÚP EM BÀI GIẢI PT VÀ CÂU C,D,E BÀI 2 VỚI Ạ..
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
Đúng 2
Bình luận (0)
Hi mọi người giải giúp em với ạ🙆♂️ cái câu D bài 1 chỗ gạch đỏ kia là dấu + nha mọi người. Em cảm ơn trước ạ😘❤
Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)
Đúng 0
Bình luận (0)






