Cho hàm số y=f(x) xác định bởi công thức: \(y=\frac{-18}{\left|2x-1\right|}\)
a) Tìm đk xác định và tập xác định của hàm số.
b) Biết \(x\in\left\{-4;-2;-1;0;1;2;3\right\}\). Hãy viết tập hợp các cặp số xác định bởi hàm số y=f(x)
Cho hàm số y=f(x) xác định bởi công thức: \(y=\frac{-18}{\left|2x-1\right|}\)
a) Tìm đk xác định và tập xác định của hàm số.
b) Biết \(x\in\left\{-4;-2;-1;0;1;2;3\right\}\). Hãy viết tập hợp các cặp số xác định bởi hàm số y=f(x)
Câu a mình làm đc r, nhờ m.n làm hộ mình câu b và ý nhỏ này nx nhé, cũng nằm trong bài.
c) Tìm \(x\in Z\) để hàm số y=f(x) đạt GTNN? Tính giá trị đó.
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
a) Tìm tập xác định của mỗi hàm số đã cho.
b) Mỗi hàm số trên liên tục trên những khoảng nào? Giải thích.
a) • \(y = f\left( x \right) = \frac{1}{{x - 1}}\)
ĐKXĐ: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)
Vậy hàm số có tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
• \(y = g\left( x \right) = \sqrt {4 - x} \)
ĐKXĐ: \(4 - x \ge 0 \Leftrightarrow x \le 4\)
Vậy hàm số có tập xác định: \(D = \left( { - \infty ;4} \right]\).
b) • Với mọi \({x_0} \in \left( { - \infty ;1} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{x - 1}} = \frac{{\mathop {\lim }\limits_{x \to {x_0}} 1}}{{\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1}} = \frac{1}{{{x_0} - 1}} = f\left( {{x_0}} \right)\)
Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;1} \right)\).
Tương tự ta có hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1; + \infty } \right)\).
Ta có: Hàm số không xác định tại điểm \({x_0} = 1\)
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x - 1}} = - \infty \)
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
Vậy hàm số \(y = f\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
• Với mọi \({x_0} \in \left( { - \infty ;4} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 4 - \mathop {\lim }\limits_{x \to {x_0}} x} = \sqrt {4 - {x_0}} = g\left( {{x_0}} \right)\)
Vậy hàm số \(y = g\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;4} \right)\).
Ta có: \(g\left( 4 \right) = \sqrt {4 - 4} = 0\)
\(\mathop {\lim }\limits_{x \to {4^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {4^ - }} 4 - \mathop {\lim }\limits_{x \to {4^ - }} x} = \sqrt {4 - 4} = 0 = g\left( 4 \right)\)
Vậy hàm số \(y = g\left( x \right)\) liên tục tại điểm \({x_0} = 4\).
Hàm số không xác định tại mọi \({x_0} \in \left( {4; + \infty } \right)\) nên hàm số \(y = g\left( x \right)\) không liên tục tại mọi điểm \({x_0} \in \left( {4; + \infty } \right)\).
Vậy hàm số \(y = g\left( x \right)\) liên tục trên nửa khoảng \(\left( { - \infty ;4} \right]\).
Cho hàm số \(y=f\left(x\right)\) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình \(f'\left(x\right)=0\) có 3 nghiệm \(x=-3\) ; \(x=0\) ; \(x=2\). Xét hàm số \(y=g\left(x\right)=f\left(x^2+4x-m\right)\), tính tổng các giá trị nguyên của tham số \(m\in[-10;10]\) để phương trình \(g'\left(x\right)=0\) có đúng 5 nghiệm phân biệt .
A. -6 B. 42 C. 50 D. 6
P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà Nội
Em xin nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán, em cám ơn nhiều ạ!
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
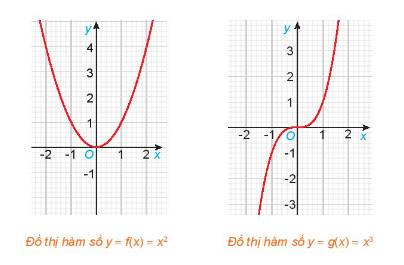
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ
Cho hàm số \(f\left(x\right)\) xác định trên tập số nguyên và nhận giá trị cũng trong tập số nguyên, thỏa mãn \(\left\{{}\begin{matrix}f\left(1\right)=0\\f\left(m+n\right)=f\left(m\right)+f\left(n\right)+3\left(4mn-1\right)\end{matrix}\right.\) với mọi m, n là số nguyên. Tính \(f\left(20\right)\)
\(f\left(20\right)=f\left(1\right)+f\left(19\right)+3\left(4.1.19-1\right)=f\left(19\right)+12.19-3\)
\(f\left(19\right)=f\left(18\right)+12.18-3\)
\(f\left(18\right)=f\left(17\right)+12.17-3\)
.....
\(f\left(3\right)=f\left(2\right)+12.2-3\)
\(f\left(2\right)=f\left(1\right)+12-3\)
Cộng vế theo vế các đẳng thức trên:
\(f\left(2\right)+f\left(3\right)+...+f\left(20\right)=f\left(1\right)+f\left(2\right)+...+f\left(19\right)+12\left(1+2+...+19\right)-3.20\)
\(\Leftrightarrow f\left(20\right)=2220\)
Đoạn này bạn tính kĩ một chút nha, mình tính không biết có sai không.
Cho hàm số \(y=f\left(x\right)=ax\left(a\ne0\right)\) xác định với mọi \(x\in Q\)
Tìm giá rị của a để \(f\left(x_1\right)\cdot f\left(x_2\right)=f\left(x_1\cdot x_2\right)\)
Giúp mình với :3
\(f\left(x_1\right)=ax_1\) ; \(f\left(x_2\right)=ax_2\) ; \(f\left(x_1x_2\right)=ax_1x_2\)
Để \(f\left(x_1\right)f\left(x_2\right)=f\left(x_1x_2\right)\)
\(\Leftrightarrow ax_1.ax_2=ax_1x_2\)
\(\Leftrightarrow a^2x_1x_2=ax_1x_2\)
\(\Leftrightarrow a^2=a\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=1\end{matrix}\right.\)
Vậy \(a=1\)
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):
a. \(y=f\left(x\right)=\dfrac{3x+1}{x^2+2\left(m-1\right)x+m^2+3m+5}\)
b. \(y=f\left(x\right)=\sqrt{x^2+2\left(m-1\right)x+m^2+m-6}\)
c. \(y=f\left(x\right)=\dfrac{3x+5}{\sqrt{x^2-2\left(m+3\right)x+m+9}}\)
a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)
cho hàm số \(y=f\left(x\right)=\frac{2x^2+6\sqrt{\left(x^2+1\right)\left(x-2\right)}+5}{x^2+3x-4}\)
a. tìm tập xác định của hàm số y=f(x)
b. CMR : \(y\le3\)
a: ĐKXĐ: (x+4)(x-1)<>0
hay \(x\notin\left\{-4;1\right\}\)
b: \(y-3=\dfrac{2x^2+6\sqrt{\left(x^2+1\right)\left(x-2\right)}+5-3x^2-9x+12}{x^2+3x-4}\)
\(=\dfrac{-x^2-9x+17+6\sqrt{\left(x^2+1\right)\left(x-2\right)}}{x^2+3x-4}< =0\)
=>y<=3
Cho hàm số \(y=f\left(x\right)=ax^2+bx+c\)
Xác định các hệ số \(a,b,c\) biết \(f\left(0\right)=1\),\(f\left(1\right)=2\),\(f\left(2\right)=4\)
Giúp mình với :3?
f(0) = 1
\(\Rightarrow\) a.02 + b.0 + c = 1
\(\Rightarrow\) c = 1
Vậy hệ số a = 0; b = 0; c = 1
f(1) = 2
\(\Rightarrow\) a.12 + b.1 + c = 2
\(\Rightarrow\) a + b + c = 2
Vậy hệ số a = 1; b = 1; c = 1
f(2) = 4
\(\Rightarrow\) a.22 + b.2 + c = 4
\(\Rightarrow\) 4a + 2b + c = 4
Vậy hệ số a = 4; b = 2; c = 1
Chúc bn học tốt! (chắc vậy :D)
Tìm tập xác định của hàm số
\(y=f\left(x\right)=\dfrac{\sqrt{4\pi^2-x^2}}{cos\left(x\right)}\)
Hàm số xác định khi: \(\left\{{}\begin{matrix}4\pi^2-x^2\ge0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2\pi\le x\le2\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)